4.4 Mesures de la tendance centrale
4.4.3 Calcul du mode
Début du texte
Lorsqu’il est unique, le mode est la valeur d’une variable la plus souvent observée dans un ensemble de données et il peut alors être considéré comme une mesure de tendance centrale, au même titre que la moyenne et la médiane. Il est toutefois possible qu’il n’y ait aucun mode ou qu’il y ait plusieurs modes.
Il n’y a aucun mode lorsque toutes les valeurs possibles apparaissent le même nombre de fois dans l’ensemble de données. Il y a plusieurs modes lorsque la fréquence la plus élevée a été observée pour plusieurs valeurs différentes. Dans les cas où il n’y a aucun mode ou plusieurs modes, le mode ne peut pas être utilisé pour situer le centre de la distribution.
Le mode peut être utilisé pour résumer des variables catégoriques, alors que la moyenne et la médiane ne peuvent être calculées que pour les variables numériques. C’est d’ailleurs le principal avantage de cette mesure. Il est aussi utile pour les variables discrètes et pour les variables continues lorsqu’elles sont présentées par intervalles.
Voici quelques exemples de calcul du mode pour une variable discrète.
Exemple 1 – Nombre de buts dans un tournoi de hockey
Lors d’un tournoi de hockey, Audrey a compté 7, 5, 0, 7, 8, 5, 5, 4, 1 et 5 buts en dix parties. Une fois les données résumées dans un tableau de fréquences, il est facile de voir que le mode du nombre de buts d’Audrey sur les 10 parties est de 5, puisque cette valeur apparaît le plus souvent (4 fois). Le mode peut être considéré comme une mesure de tendance centrale pour cet ensemble de données, car il est unique.
| Nombre de buts | Fréquence (nombre de parties) |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 4 | 1 |
| 5 | 4 |
| 7 | 2 |
| 8 | 1 |
| 0 zéro absolu ou valeur arrondie à zéro | |
Exemple 2 – Nombre de points en douze parties de basket-ball
En 12 parties de basket-ball, Gabriel a compté 14, 14, 15, 16, 14, 16, 16, 18, 14, 16, 16 et 14 points. Une fois les données résumées dans un tableau de fréquences, il est facile de voir que cet ensemble de données est bimodal, c’est-à-dire qu’il y a deux modes, 14 et 16, parce que ce sont les valeurs les plus souvent observées (elles apparaissent 5 fois chacune). Le mode ne peut pas être utilisé comme mesure de tendance centrale, car il y en a plus d’un. Il s’agit d’une distribution bimodale.
| Nombre de points | Fréquence (nombre de parties) |
|---|---|
| 14 | 5 |
| 15 | 1 |
| 16 | 5 |
| 18 | 1 |
Exemple 3 – Nombre de touchés au cours de la saison de football
L’ensemble de données qui suit représente le nombre de touchés que Jérôme a marqué au cours de la saison de football : 0, 0, 1, 0, 0, 2, 3, 1, 0, 1, 2, 3, 1, 0. Comparons la moyenne, la médiane et le mode.
La somme ces valeurs est de 14 et le nombre de valeurs est de 14. La moyenne est donc égale à 1. Étant donné que le nombre de données est pair, la médiane sera égale à la moyenne entre la 7e et la 8e valeur une fois les données ordonnées :
| Rang | Nombre de touchés |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 11 | 2 |
| 12 | 2 |
| 13 | 3 |
| 14 | 3 |
Elle est donc égale à 1. Une fois les données résumées dans un tableau de fréquences, on peut voir que le mode est quant à lui égal à 0.
| Nombre de touchés | Fréquence (nombre de parties) |
|---|---|
| 0 | 6 |
| 1 | 4 |
| 2 | 2 |
| 3 | 2 |
| 0 zéro absolu ou valeur arrondie à zéro | |
En résumé, dans cet exemple, la moyenne est égale à 1, la médiane est égal à 1 et le mode est égal à 0.
Le mode est moins utilisé pour les variables continues, car il est probable qu’aucune valeur ne revienne plus d’une fois. Par exemple, si on demande à 20 personnes leur revenu exact au dollar près au cours de la dernière année, il se peut que certains aient des revenus très près les uns des autres, mais qu’ils ne soient jamais exactement le même. On peut alors utiliser des intervalles et déterminer la classe modale. L’histogramme permet de visualiser facilement la classe modale d’une variable continue.
Exemple 4 – Taille des personnes présentes à une partie de basketball
On s’intéresse à la taille des personnes présentes dans l’aréna lors d’une partie de basketball. Le tableau 4.4.3.5 présente le nombre de personnes pour chaque intervalle de 20 centimètres de la taille dans un jeu de données. La classe modale serait l’intervalle de 160 à 179 cm, car c’est celle avec la fréquence la plus élevée.
| Taille (en centimètre) | Fréquence (nombre de personnes) |
|---|---|
| 20 to 39 | 42 |
| 40 to 59 | 105 |
| 60 to 79 | 176 |
| 80 to 99 | 230 |
| 100 to 119 | 214 |
| 120 to 139 | 168 |
| 140 to 159 | 363 |
| 160 to 179 | 480 |
| 180 to 200 | 170 |
| 200 to 219 | 11 |
Le graphique 4.4.3.1 présente ces données sous la forme d’un histogramme.
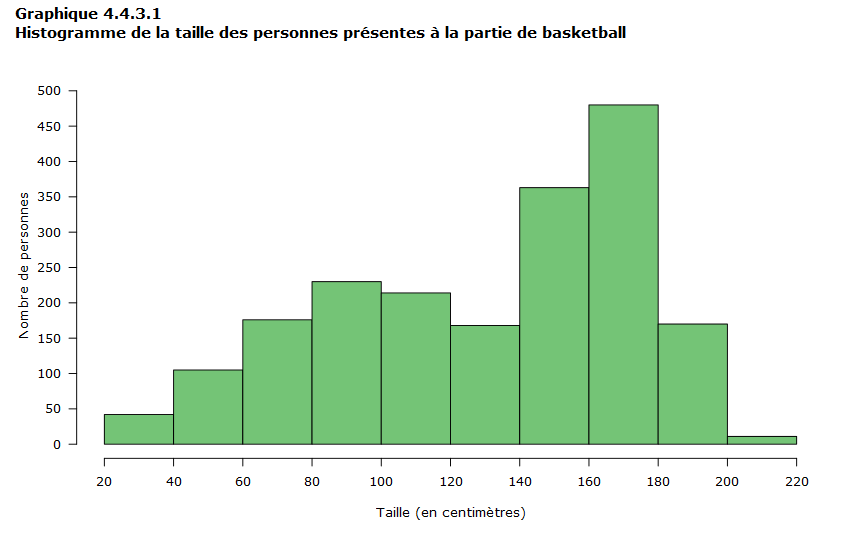
Tableau de données du graphique 4.4.3.1
Les données illustrées par ce graphique sont celles du tableau 4.4.3.5.
En observant l’histogramme, on peut clairement identifier la classe modale, 160 à 179, qui a une fréquence de 480. Cependant, on s’aperçoit que la fréquence diminue lorsque l’on passe à l’intervalle 140 à 159 (363) et diminue davantage à l’intervalle 120 à 139 (168), mais ensuite qu’elle remonte jusqu’à l’intervalle 80 à 99 (230).
Pour les variables catégoriques ou discrètes, les modes multiples correspondent à la même fréquence (la plus grande). Pour les variables continues, tous les sommets de la distribution peuvent être considérés comme des modes, même lorsqu’ils correspondent à des hauteurs différentes sur l’histogramme. La distribution de cet exemple serait donc bimodale, avec un mode majeur au niveau de la classe 160 à 179 et un mode mineur situé au niveau de la classe 80 à 99. La classe modale ne doit pas être utilisée comme mesure de tendance centrale, mais la découverte de deux modes nous donne une indication qu’il existe possiblement deux groupes distincts dans les données qui devraient être analysés séparément.
- Date de modification :