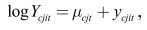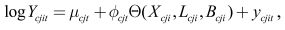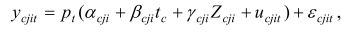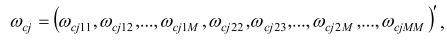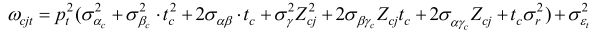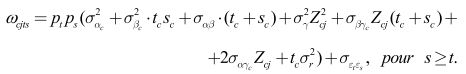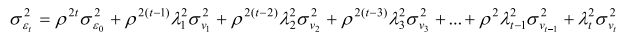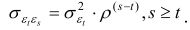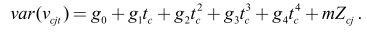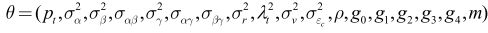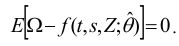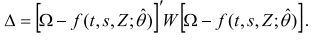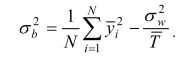4 Méthode d'estimation
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
Considérons maintenant un immigrant i arrivé dans l'année c (il est membre de la cohorte d'arrivée c ) à l'âge j . On peut décrire les gains de l'intéressé dans l'année t avec suffisamment de souplesse en prenant
où μ cjt est la moyenne des gains en expression logarithmique dans chaque cellule cjt . L'équation (4) est l'équation d'estimation de premier stade qui extrait la composante des gains individuels de la dynamique des gains de la cohorte d'arrivée. Il est normal de procéder en deux étapes chez les auteurs qui étudient l'inégalité et l'instabilité des gains, mais dans certaines études on obtient y ˆ cjit par régression du logarithme des gains sur un polynôme de l'âge (Haider, 2001; Beach, Finnie et Gray, 2003; Morissette et Ostrovsky, 2005). Cette orientation paraît conférer plus de polyvalence dans le contexte de la présente étude.
Après avoir tiré y ˆ cjit de la régression de premier stade, il est possible d'en décomposer la variance en un facteur « inter » et un facteur « intra ». Dans la partie descriptive de l'étude, nous posons simplement (comme dans Beach, Finnie et Gray, 2003, et dans Morissette et Ostrovsky, 2005) que ycjit = y cji + vcjit et nous calculons les facteurs « inter » et « intra » par les formules de Johnston (1984) 3 .
Dans une observation de différentes cohortes d'arrivée sur différentes suites numériques d'années (la cohorte de 1980 à 1982 sera observée sur 22 ans et la cohorte de 1998 à 2000, sur 4 ans seulement), il serait difficile d'établir une comparaison d'inégalité et d'instabilité entre cohortes s'il fallait calculer pour toutes les périodes t où les cohortes sont observées. Pour que les résultats soient plus comparables entre cohortes, le calcul de décomposition se fait pour un certain nombre de périodes postérieures à l'arrivée : t =4 (ensemble des cohortes), t =7 (ensemble des cohortes saufla cohorte de 1998 à 2000) et t =10 (ensemble des cohortes saufles cohortes de 1995 à 1997 et de 1998 à 2000). Par exemple, si t =4, la variance de la cohorte d'arrivée de 1980 à 1982 sera calculée pour 1983, 1984, 1985 et 1986; pour la cohorte de 1983 à 1985, elle le sera pour 1986, 1987, 1988 et 1989. Il s'agit de panels non équilibrés, puisqu'un panel sur quatre ans comprend aussi les unités présentes pendant deux ou trois périodes seulement. De même, un panel sur sept ans comprendrait les unités observées pendant cinq ou six périodes et un panel sur dix ans, celles qui l'ont été pendant huit ou neuf périodes.
Comme nous l'avons mentionné en introduction, notre propos est non seulement de décrire l'inégalité et l'instabilité des gains des immigrants, mais aussi d'en analyser les causes possibles et, en particulier, le rôle joué par la scolarisation à l'étranger, la compétence linguistique et le pays d'origine. Il est possible d'estimer les effets de ces variables en ajoutant des variables de contrôle à l'équation de premier stade, en réestimant ycjit et en utilisant les nouvelles estimations dans une autre étape. Plus précisément, l'équation (4) prend la forme
où Xcji est le nombre d'années de scolarité à l'étranger, où Lcji est un jeu de variables fictives pour la capacité de parler l'une et/ou l'autre des langues officielles et où Bcji est l'ensemble de variables fictives de la région d'origine. On peut estimer un modèle qui comprend Xcji, Lcji, Bcji ou toutes ces variables. De là, il devient possible non seulement de comparer les mesures d'inégalité et d'instabilité des gains entre cohortes et âges d'arrivée, mais aussi de voir dans quelle mesure l'inégalité et l'instabilité subissent l'influence de ces variables dans chacune des cohortes. Une telle analyse peut se révéler particulièrement utile au Canada où un régime de sélection des immigrants par évaluation numérique 4 vient récompenser la scolarité acquise à l'étranger et la capacité de parler une des langues officielles du pays.
Cette méthode d'analyse de l'inégalité et de l'instabilité est fort simple et fait appel à l'intuition, mais elle présente aussi des inconvénients évidents. D'abord et avant tout, elle ne permet pas de cerner l'évolution temporelle ni de la composante permanente ni de la composante temporaire. Elle ne laisse aucune place à l'hétérogénéité des taux de croissance des gains (par opposition à l'hétérogénéité des niveaux). Enfin, elle ne tient pas compte de tout ce qui est corrélation sériale dans la composante temporaire. Nous allons donc considérer un modèle plus polyvalent d'après les modèles de Haider (2001) et de Baker et Solon (2003).
Comme dans (2), nous posons que les gains individuels de la ce cohorte d'arrivée à l'âge d'arrivée j (nombre d'années) prennent la forme
où ucjit = ucjit, −1 + rcjit et où ε cjit = ρε cjit, −1 + λ tvcjit . Ainsi, l'expérience professionnelle totale se divise en deux, à savoir (1) l'expérience canadienne tc, qui est la même pour tous les membres de la ce cohorte d'arrivée, et (2) l'expérience qui a pu être acquise à l'étranger Zcji et qui est simplement définie comme l'âge d'arrivée, moins 25.
À partir des résidus en (4), on établit une matrice des autocovariances d'échantillon pour chaque cohorte et chaque âge d'arrivée. Pour les immigrants arrivés à l'âge de 30 ans pendant la période de 1980 à 1982, il s'agira d'une matrice 22×22 ( t= 1983, 1984,…, 2004) et, pour les immigrants correspondants de la période de 1995 à 1997, d'une matrice 7×7 ( t= 1998, 1999, …, 2004). La taille de la matrice dépendra tant de c que de j ; comme le nombre total de cohortes d'arrivée est de sept, il y aura pour j ∈ [ ] 25,49 7×25=175 matrices des autocovariances Ω cj au total, ce qui donnera 13 615 moments d'échantillon.
Soit ωcj un vecteur d'éléments uniques de Ω cj,
où M×M est la taille de chaque matrice Ω cj qui dépend de c et j . Tous les ω cj peuvent se combiner en un même vecteur Ω de sorte que chaque élément diagonal ω cjt dans Ω cj puisse se formuler comme
et chaque élément extradiagonal ω cjts comme
La composante temporaire de la variance ε cjit = ρε cjit, −1 + λ t ν cjit prend la forme
et la covariance, la forme
Comme dans Baker et Solon (2003), σ 2v peut se modéliser comme fonction quadratique ou quartique de t et Zcj . En particulier, il peut se formuler comme
Si on pose que Ω* = fts (,, Z ;θ) est l'analogue de Ω au niveau de la population, on peut alors estimer le jeu de paramètres de modélisation
par la méthode généralisée des moments (MGM) avec 13 615 moments d'échantillon correspondant à 13 615 éléments de Ω
On peut estimer les paramètres en (12) à l'aide d'un estimateur de distance minimale MGM. On choisit un jeu optimal d'estimations paramétriques θ ˆ en minimisant
Haider (2001) et Baker et Solon (2003) font voir les avantages de prendre une matrice unité comme matrice de pondération au lieu de W (voir aussi Altonji et Segal, 1996, et Clark, 1996). Une cause particulière de perte d'efficience avec un estimateur de minimisation de distance en
équipondération est qu'on ne tient pas compte de ce que les éléments ω cj de Ω sont fondés sur un nombre différent d'observations. L'estimateur sera plus efficient si on pondère les moments d'échantillon en proportion de la taille de chaque cellule cj . Les résultats d'estimation de notre étude viennent d'un estimateur de distance minimale avec une matrice unité comme matrice de pondération et aussi avec une matrice de pondération des moments par les tailles d'échantillon.
On peut voir en (7) que, en établissant p1983 =1 ( t =0), on caractérise σ α2 dans un modèle à paramètre unique dans le terme de croissance. Avec un modèle entier à paramètres
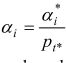 , où t* est le premier
facteur de saturation pour la cohorte à laquelle appartient
i . Pour la cohorte de 1980 à 1982, t*=
1983 et, pour la cohorte de 1983 à 1985, t*= 1986,
pour ne citer que ces exemples. On peut maintenant exprimer un
élément diagonal dans Ω cjt
comme
, où t* est le premier
facteur de saturation pour la cohorte à laquelle appartient
i . Pour la cohorte de 1980 à 1982, t*=
1983 et, pour la cohorte de 1983 à 1985, t*= 1986,
pour ne citer que ces exemples. On peut maintenant exprimer un
élément diagonal dans Ω cjt
comme
Pour Zcj =0, la composante permanente de la variance pour la cohorte de 1980 à 1982 en 1983
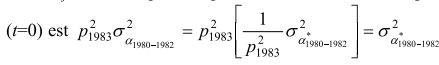 ; pour la cohorte de 1983 à
1985, elle est
; pour la cohorte de 1983 à
1985, elle est 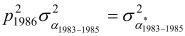 . En d'autres termes, tous les
. En d'autres termes, tous les
de saturation pour les cohortes représentées. On peut prendre les estimations de
3 . Le facteur intra se calcule par
et le facteur inter, par
4. Le système d'évaluation numérique adopté au Canada en 1967 prévoit plus de points pour les demandeurs s'ils ont un niveau de scolarité plus élevé, s'ils connaissent mieux les langues officielles (français et anglais) et s'ils sont plus jeunes.
- Date de modification :