La modélisation espace-état appliquée aux séries chronologiques de l’Enquête sur la population active des Pays-Bas : sélection de modèles et estimation de l’erreur quadratique moyenne
Section 5. Résultats
5.1 Autres spécifications de modélisation pour
l’EPA
On choisit et évalue habituellement les modèles SCS en employant des
tests formels de diagnostic de normalité, d’homoscédasticité et d’indépendance
des innovations normalisées. Une paramétrisation parcimonieuse est fondée sur
des tests de rapport de vraisemblance logarithmique ou des critères
d’information (d’Akaike, de Bayes, etc.). Toutefois, les résultats de ces tests
et critères dépendent des estimations ponctuelles particulières des
hyperparamètres plutôt que de leurs distributions entières. Les distributions
en simulation de Monte-Carlo (décrite à la section 4) des estimateurs des
hyperparamètres nous éclairent davantage sur l’adéquation de la modélisation
SCS. Les distributions en simulation nous livrent des indices sur l’éventuelle
surspécification d’un modèle, en ce sens que certaines variables d’état
pourraient être modélisées comme invariantes dans le temps.
Dans notre étude, nous considérons quatre modèles qui diffèrent pour
le nombre d’hyperparamètres à estimer par la méthode du maximum de
vraisemblance. Le modèle le plus complet, le modèle 1, est actuellement
utilisé par Statistics Netherlands, mais après retrait de la composante de bruit
blanc
du paramètre réel de
population
On a constaté que cette
composante avait une variance excessivement élevée et représentait une
estimation perturbée d’autres hyperparamètres marginalement significatifs
(variances de perturbation du BRE et de la composante saisonnière) dans le cas
de l’EPA. En retranchant la composante irrégulière
du modèle, on atténue
l’instabilité des deux hyperparamètres précités. Cette formulation implique que
le paramètre de population
n’accuse pas d’irrégularités
impossibles à appréhender par la structure stochastique de la tendance et de la
composante saisonnière. L’adoption de cette hypothèse peut être favorisée par
une rigidité relative du marché du travail. L’évolution des niveaux de chômage
est normalement progressive et doit donc être largement intégrée aux mouvements
de la tendance stochastique. Les trois autres modèles sont des cas d’espèce du
modèle 1, tous avec la composante irrégulière
en moins (voir
tableau 5.1).
Tableau 5.1
Hyperparamètres estimés dans les quatre versions du modèle EPA; les variances de perturbation sont estimées à l’échelle logarithmique
Sommaire du tableau
Le tableau montre les résultats de Hyperparamètres estimés dans les quatre versions du modèle EPA; les variances de perturbation sont estimées à l’échelle logarithmique . Les données sont présentées selon Modèles (titres de rangée) et Description et Paramètres estimés(figurant comme en-tête de colonne).
| Modèles |
Description |
Paramètres estimés |
| M1 |
Modèle complet |
|
| M2 |
Modèle saisonnier indépendant du temps |
|
| M3 |
Modèle BRE indépendant du temps |
|
| M4 |
Modèle saisonnier et BRE indépendant du temps |
|
Les distributions simulées des estimateurs des hyperparamètres dans
le modèle 1 montrent que les hyperparamètres de variance pour la
composante saisonnière et, en particulier, pour le BRE sont souvent estimés
comme étant proches de zéro. Cela cause une bimodalité dans la distribution de
ces estimations de variance avec une masse significative concentrée près de
zéro. De plus, une tentative d’estimation de
ainsi que de
comme dans le modèle 1,
cause une distorsion dans la distribution des estimateurs de maximum de
vraisemblance des autres hyperparamètres, laquelle devrait être normale. Ainsi,
la normalité dans
et
est gravement compromise avec
des valeurs aberrantes extrêmes et/ou un énorme coefficient d’applatissement (voir
la figure A.1 en annexe où l’axe des x est étiré à cause des valeurs
aberrantes), alors que les variances correspondantes sont moins susceptibles de
présenter des valeurs extrêmes, étant censées fluctuer autour de l’unité. Si on
rend la composante saisonnière invariante dans le temps comme dans le
modèle 2, on ne change guère la situation des hyperparamètres de la
tendance et du BRE. On pourrait même y voir un traitement moins qu’optimal, car
les valeurs aberrantes sont plus extrêmes et le coefficient d’applatissement
est excessif dans la distribution des cinq hyperparamètres des erreurs
d’enquête (figure A.2). Par contraste, nous avons pu constater (voir les
figures A.3 et A.4) que, dans les deux modèles où la composante BRE est
fixe dans le temps (modèles 3 et 4), toutes les estimations des
hyperparamètres correspondant aux erreurs d’enquête étaient en distribution
normale. Dans le modèle 3, les distributions demeurent asymétriques pour
la pente et la composante saisonnière (asymétrie de -0,88 et -0,72 et
applatissement de 5,56 et 4,61 respectivement). En fixant à zéro
l’hyperparamètre saisonnier dans le modèle 4, l’amélioration est seulement
marginale et la distribution de
présente un coefficient
négatif d’asymétrie (-0,81) et un coefficient excessif d’applatissement (1,76).
Ces données de simulation semblent indiquer que, dans la
modélisation des séries EPA, la préférence pourrait aller au modèle 3 plus
parcimonieux, où la seule variance de perturbation BRE est fixée à zéro, mais
comme le BRE même dépend du nombre de chômeurs, Statistics Netherlands conserve
la variance de cet hyperparamètre à des fins de production afin de garder une
souplesse suffisante devant l’évolution progressive du processus sous-jacent.
On peut recourir au test du rapport de vraisemblance pour vérifier
si les hyperparamètres de la composante saisonnière et du BRE sont
significativement différents de zéro, les modèles 2 à 4 étant imbriqués
dans le modèle 1. La variable à tester comporte des valeurs très basses
pour les trois autres modèles (0; 0,18 et 0,18 encore pour les modèles 2, 3 et 4,
l’absence de différences entre les modèles 2 et 1 et entre les
modèles 3 et 4 étant attribuable à la très faible valeur de
l’hyperparamètre de la composante saisonnière). Ainsi, ces tests n’indiquent
pas que les modèles plus parcimonieux présentent des résultats inférieurs à
ceux du modèle 1. Une autre façon d’évaluer l’adéquation des quatre
modèles est de les comparer sous l’angle de leur valeur prévisionnelle par la
racine carrée des différences quadratiques moyennes (RDQM) entre les
estimations ERG et les prédictions des signaux à un pas avant. On peut le faire
pour chaque vague séparément :
étant égal à 20, 30 et
60 mois. Les résultats figurant en annexe (tableau B.1) montrent
cependant qu’il n’y a guère de différence de rendement des quatre modèles dans
leur application à la série initiale. Les modèles plus parcimonieux font voir
une légère augmentation de la RDQM.
Les reformulations de modèle ne semblent pas influer sur la distribution
de l’estimateur du paramètre autorégressif
des erreurs d’enquête sur les
1 000 séries simulées : on approche d’assez près la distribution
normale et les valeurs vont de 0 à 0,4 quand
ce qui s’accorde avec
l’approximation de sa distribution asymptotique à la sous-section 3.3. L’intervalle
des valeurs est un peu plus étendu pour les séries temporelles plus courtes et
plus étroites quand
Nous exécutons séparément
pour les quatre modèles la procédure de simulation décrite dans la section
précédente et l’analyse des méthodes bootstrap.
5.2 Estimation EQM
L’objet de notre étude par simulation est l’estimation EQM de la
tendance et du signal de population, ce dernier étant la somme de la tendance
et de la composante saisonnière. Nous évaluons le rendement du filtre de Kalman
et des cinq méthodes d’estimation EQM à la section 3 en considérant le
biais relatif et les EQM des estimateurs EQM. D’abord, nous prenons la moyenne
des estimations EQM filtrées en (3.3), (3.4) et (3.7) sur les 1 000 simulations
(la moyenne est indiquée par la barre sur
alors que, dans le cas des
estimations EQM par filtre de Kalman, nous l’établissons sur 10 000 simulations,
comme nous l’avons mentionné au début de la section 4. Ces estimations EQM
filtrées et mises en moyenne pour le modèle 3 (sauf pour la méthode AA; voir
l’explication plus loin) sont décrites aux figures 5.1 à 5.4 pour
et
respectivement. Nous sautons
les
premiers points temporels de
l’échantillon
devrait dépasser le nombre de
points temporels nécessaires au début de la série pour éliminer l’effet d’une
initialisation diffuse par le filtre). À noter que l’analyse est fondée sur des
estimations filtrées plutôt que lissées, car ce sont les premières qui
reproduisent le mieux le processus de production des chiffres officiels. Les
EQM des quatre figures sont en configuration décroissante, comme on pouvait s’y
attendre, parce que des estimations filtrées augmentent en précision si on
dispose de plus d’information dans le temps pour estimer les variables d’état.
Une exception à la règle, ce sont les EQM réelles de la figure 5.2. Une
explication possible est que, dans cette application, les EQM des signaux sont
proportionnelles aux signaux mêmes par les erreurs-types fondées sur le plan et
que les EQM réelles reposent sur un autre ensemble (bien plus étendu) de séries
simulées (50 000 pour les EQM réelles et 1 000 pour les EQM estimées).
On remarquera que les traits de la figure 5.1 paraissent bien plus lisses,
puisqu’ils s’étendent sur moins de points temporels. Ajoutons que, dans les
figures 5.2 et 5.3, la configuration semble plus irrégulière, l’échelle de
l’axe des y étant plus fine si on compare ces
figures aux figures 5.1 et 5.4.
Nous calculons le biais relatif en pourcentage comme
où
correspond à une méthode
d’estimation particulière et où
est défini en (4.2). Les
biais EQM relatifs en pourcentage et en moyenne dans le temps (après retrait
des
premiers points temporels) pour
le signal, la tendance et la composante saisonnière sont présentés aux tableaux 5.2,
5.3, 5.4 et 5.5.
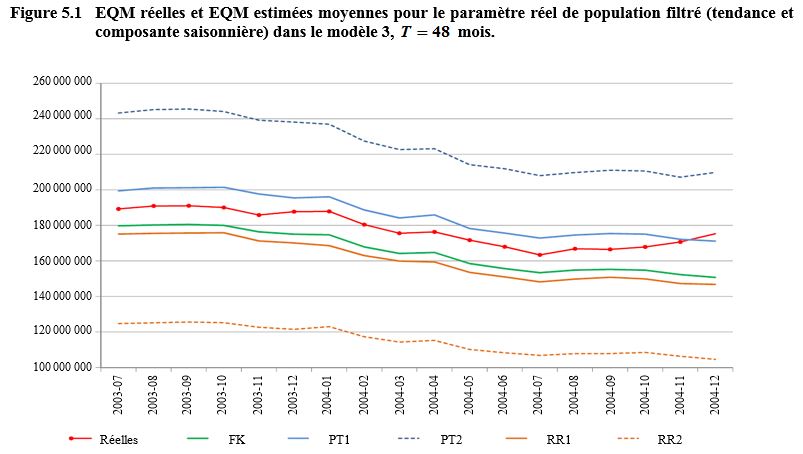
Description de la figure 5.1
Figure illustrant les EQM réelles
et les EQM estimées moyennes pour le paramètre réel de population filtré dans
le modèle 3, T = 48 mois. L’EQM est
sur l’axe des y allant de 100 000 000 à environ 250 000 000.
Le temps est sur l’axe des x allant de juillet 2003 à décembre 2004. La figure
présente six courbes, une pour les EQM réelles et cinq pour les EQM estimées
suivantes : filtre de Kalman (FK), Rodriguez et Ruiz 1 et 2 (RR1 et RR2)
et Pfeffermann et Tiller 1 et 2 (PT1 et PT2). Les EQM décroissent avec le
temps, sauf vers la fin pour les EQM réelles. Les niveaux des EQM sont, en
ordre décroissant, PT2, PT1, Réelles, FK, RR1 et RR2.
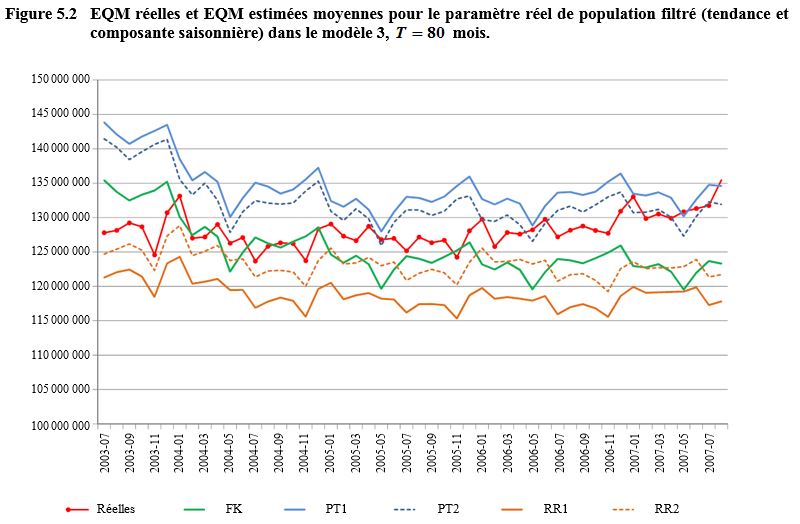
Description de la figure 5.2
Figure illustrant les EQM réelles
et les EQM estimées moyennes pour le paramètre réel de population filtré dans
le modèle 3, T = 80 mois. L’EQM est
sur l’axe des y allant de 115 000 000 à environ 145 000 000.
Le temps est sur l’axe des x allant de juillet 2003 à juillet 2007. La figure
présente six courbes, une pour les EQM réelles et cinq pour les EQM estimées
suivantes : filtre de Kalman (FK), Rodriguez et Ruiz 1 et 2 (RR1 et RR2)
et Pfeffermann et Tiller 1 et 2 (PT1 et PT2). Les EQM décroissent avec le
temps, sauf pour la seconde moitié des EQM réelles. Les niveaux des EQM sont,
en ordre décroissant, PT1, PT2, Réelles, FK, RR2 et RR1.
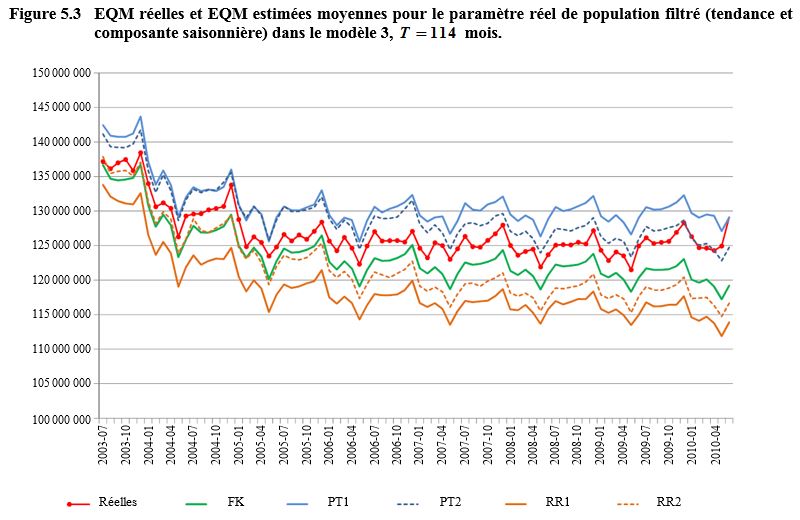
Description de la figure 5.3
Figure illustrant les EQM réelles
et les EQM estimées moyennes pour le paramètre réel de population filtré dans
le modèle 3, T = 114 mois. L’EQM est
sur l’axe des y allant de 110 000 000 à environ 145 000 000.
Le temps est sur l’axe des x allant de juillet 2003 à avril 2010. La figure
présente six courbes, une pour les EQM réelles et cinq pour les EQM estimées
suivantes : filtre de Kalman (FK), Rodriguez et Ruiz 1 et 2 (RR1 et RR2)
et Pfeffermann et Tiller 1 et 2 (PT1 et PT2). Les EQM décroissent avec le
temps, sauf pour la seconde moitié des EQM réelles. Les niveaux des EQM sont,
en ordre décroissant, PT1, PT2, Réelles, FK, RR2 et RR1. Les courbes sont plus
rapprochées que dans les figures précédentes.
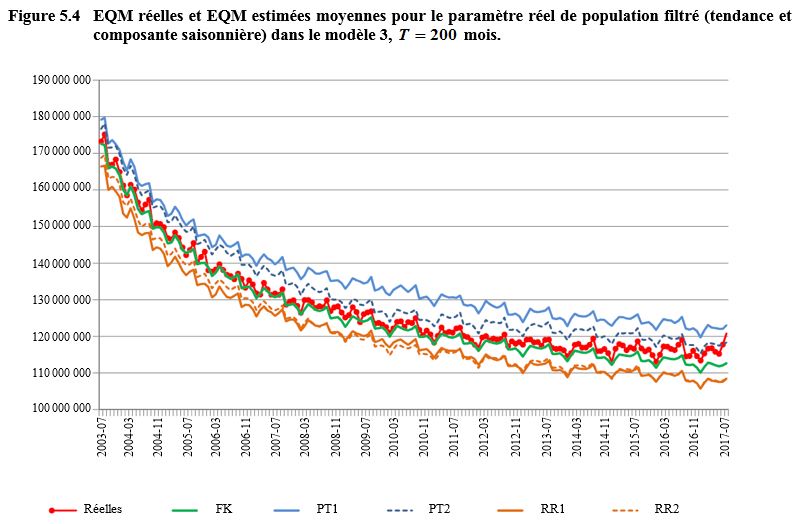
Description de la figure 5.4
Figure illustrant les EQM réelles
et les EQM estimées moyennes pour le paramètre réel de population filtré dans
le modèle 3, T = 200 mois. L’EQM est
sur l’axe des y allant de 105 000 000 à environ 180 000 000.
Le temps est sur l’axe des x allant de juillet 2003 à juillet 2017. La figure
présente six courbes, une pour les EQM réelles et cinq pour les EQM estimées
suivantes : filtre de Kalman (FK), Rodriguez et Ruiz 1 et 2 (RR1 et RR2)
et Pfeffermann et Tiller 1 et 2 (PT1 et PT2). Les EQM décroissent avec le
temps. Les niveaux des EQM sont, en ordre décroissant, PT1, PT2, Réelles, FK,
RR2 et RR1. Les courbes sont plus rapprochées que dans les figures précédentes.
Tableau 5.2
Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA,
Sommaire du tableau
Le tableau montre les résultats de Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance et Composante saisonnière(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
| FK |
S.O. |
S.O. |
-7,1 |
-7,6 |
S.O. |
S.O. |
-6,5 |
-6,6 |
S.O. |
S.O. |
-6,7 |
-7,0 |
| PT1 |
S.O. |
S.O. |
4,4 |
1,4 |
S.O. |
S.O. |
8,7 |
6,4 |
S.O. |
S.O. |
4,9 |
2,4 |
| PT2 |
S.O. |
S.O. |
26,2 |
-4,4 |
S.O. |
S.O. |
22,4 |
-3,1 |
S.O. |
S.O. |
25,6 |
-4,6 |
| RR1 |
S.O. |
S.O. |
-9,8 |
-10,8 |
S.O. |
S.O. |
-13,9 |
-13,8 |
S.O. |
S.O. |
-9,5 |
-10,1 |
| RR2 |
S.O. |
S.O. |
-35,3 |
-5,6 |
S.O. |
S.O. |
-29,9 |
-3,2 |
S.O. |
S.O. |
-29,7 |
-5,1 |
Tableau 5.3
Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA,
Sommaire du tableau
Le tableau montre les résultats de Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance et Composante saisonnière(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
| FK |
-3,0 |
-3,2 |
-2,1 |
-2,2 |
-3,5 |
-3,8 |
-2,5 |
-2,5 |
8,8 |
2,5 |
2,9 |
2,4 |
| AA |
S.O. |
S.O. |
S.O. |
14,9 |
S.O. |
S.O. |
S.O. |
15,0 |
S.O. |
S.O. |
S.O. |
14,9 |
| PT1 |
8,6 |
6,7 |
4,9 |
6,2 |
10,6 |
8,9 |
7,1 |
8,4 |
20,8 |
10,7 |
10,3 |
11,1 |
| PT2 |
4,8 |
3,7 |
1,4 |
2,1 |
4,8 |
4,9 |
2,1 |
2,3 |
17,3 |
8,2 |
6,9 |
7,1 |
| RR1 |
-7,2 |
-9,0 |
-7,3 |
-7,2 |
-9,6 |
-11,2 |
-9,6 |
-9,5 |
-3,8 |
-9,0 |
-6,7 |
-6,6 |
| RR2 |
6,7 |
-3,5 |
-3,9 |
-4,2 |
5,3 |
-4,1 |
-4,6 |
-5,4 |
18,6 |
-4,7 |
-4,1 |
-4,3 |
Tableau 5.4
Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA,
Sommaire du tableau
Le tableau montre les résultats de Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance et Composante saisonnière(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
| FK |
-2,1 |
-2,6 |
-2,4 |
-2,2 |
-2,3 |
-2,7 |
-2,4 |
-2,3 |
2,5 |
-3,2 |
-3,1 |
-2,6 |
| AA |
S.O. |
S.O. |
S.O. |
5,2 |
S.O. |
S.O. |
S.O. |
4,1 |
S.O. |
S.O. |
S.O. |
12,5 |
| PT1 |
8,1 |
5,7 |
3,3 |
5,5 |
10,0 |
7,9 |
5,2 |
7,6 |
4,9 |
1,4 |
1,4 |
0,3 |
| PT2 |
2,2 |
3,2 |
1,9 |
1,5 |
3,3 |
4,3 |
3,1 |
2,8 |
1,2 |
-2,0 |
1,0 |
0,6 |
| RR1 |
-8,3 |
-7,8 |
-6,4 |
-6,5 |
-10,7 |
-9,9 |
-8,7 |
-8,9 |
-3,1 |
-7,2 |
-5,5 |
-5,6 |
| RR2 |
-1,1 |
-6,0 |
-3,9 |
-3,5 |
-3,0 |
-7,6 |
-5,5 |
-5,0 |
7,3 |
-5,9 |
-3,2 |
-3,0 |
Tableau 5.5
Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA,
Sommaire du tableau
Le tableau montre les résultats de Biais moyen en pourcentage des estimateurs EQM dans le modèle de l’EPA. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance et Composante saisonnière(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
M1 |
M2 |
M3 |
M4 |
| FK |
-1,3 |
-1,6 |
-1,3 |
-1,3 |
-1,7 |
-1,8 |
-1,6 |
-1,6 |
3,8 |
-1,7 |
-1,6 |
-1,6 |
| AA |
S.O. |
S.O. |
S.O. |
5,9 |
S.O. |
S.O. |
S.O. |
5,6 |
S.O. |
S.O. |
S.O. |
5,6 |
| PT1 |
6,3 |
6,2 |
6,3 |
5,5 |
7,5 |
7,7 |
7,8 |
7,1 |
10,8 |
2,6 |
3,0 |
3,0 |
| PT2 |
6,8 |
4,0 |
3,0 |
2,3 |
7,6 |
4,9 |
4,2 |
3,6 |
12,5 |
2,1 |
1,3 |
0,6 |
| RR1 |
-8,0 |
-8,0 |
-4,9 |
-5,9 |
-10,0 |
-9,9 |
-6,8 |
-7,1 |
-1,1 |
-5,3 |
-3,8 |
-3,9 |
| RR2 |
-5,1 |
-5,6 |
-4,5 |
-5,0 |
-7,0 |
-7,4 |
-6,0 |
-6,4 |
3,6 |
-3,1 |
-3,3 |
-3,9 |
Tableau 5.6
Variance estimée moyenne des EQM des estimateurs EQM pour le nombre de chômeurs dans le modèle de l’EPA (division par
Sommaire du tableau
Le tableau montre les résultats de Variance estimée moyenne des EQM des estimateurs EQM pour le nombre de chômeurs dans le modèle de l’EPA (division par xxxxx. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance, Composante saisonnière, M3 et M4(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M3 |
M4 |
M3 |
M4 |
M3 |
M4 |
|
|
|
|
|
|
|
|
|
|
|
|
| PT1 |
3,39 |
3,46 |
3,64 |
3,66 |
3,61 |
3,83 |
3,67 |
3,81 |
0,59 |
0,61 |
0,64 |
0,65 |
| PT2 |
5,03 |
7,26 |
3,03 |
3,10 |
4,02 |
5,27 |
2,56 |
2,61 |
1,00 |
1,50 |
0,52 |
0,54 |
| RR1 |
2,51 |
2,83 |
2,68 |
3,06 |
2,03 |
2,51 |
2,13 |
2,62 |
0,44 |
0,51 |
0,48 |
0,55 |
| RR2 |
1,59 |
5,93 |
2,74 |
2,85 |
1,52 |
3,97 |
2,50 |
2,56 |
0,55 |
1,28 |
0,50 |
0,52 |
Tableau 5.7
Variance estimée moyenne des EQM des estimateurs EQM pour le nombre de chômeurs dans le modèle de l’EPA (division par
Sommaire du tableau
Le tableau montre les résultats de Variance estimée moyenne des EQM des estimateurs EQM pour le nombre de chômeurs dans le modèle de l’EPA (division par
. Les données sont présentées selon Modèles (titres de rangée) et Signal*, Tendance, Composante saisonnière, M3 et M4(figurant comme en-tête de colonne).
| Modèles |
SignalNote * |
Tendance |
Composante saisonnière |
| M3 |
M4 |
M3 |
M4 |
M3 |
M4 |
|
|
|
|
|
|
|
|
|
|
|
|
| PT1 |
2,24 |
2,29 |
2,43 |
2,52 |
1,82 |
1,91 |
1,97 |
2,09 |
0,27 |
0,30 |
0,27 |
0,31 |
| PT2 |
2,20 |
2,23 |
2,14 |
2,18 |
1,71 |
1,74 |
1,66 |
1,69 |
0,27 |
0,28 |
0,27 |
0,29 |
| RR1 |
1,86 |
1,95 |
1,74 |
1,82 |
1,42 |
1,56 |
1,33 |
1,46 |
0,22 |
0,23 |
0,22 |
0,23 |
| RR2 |
1,98 |
2,01 |
1,94 |
1,97 |
1,57 |
1,60 |
1,49 |
1,54 |
0,23 |
0,23 |
0,23 |
0,23 |
Voici les principales conclusions de notre étude par
simulation :
1. Pour
et en moyenne dans le temps (à partir de
le biais relatif de l’EQM du signal après application
du filtre de Kalman est d’environ -7 %. Ce biais tend à décroître à mesure
que s’allonge la série. Le biais de filtre de Kalman (FK) est des plus modestes
quand
et la situation est telle qu’aucune des méthodes
d’estimation n’offre d’amélioration par rapport aux estimations EQM par filtre
de Kalman. Nous pourrions toujours appliquer la meilleure méthode d’estimation
avec des biais positifs pour dégager une plage de valeurs contenant l’EQM
réelle.
2. Nous
avons pu voir que la méthode AA (approximation
asymptotique) est inapplicable aux modèles comportant des hyperparamètres
marginalement significatifs. Quand on estime que certains des hyperparamètres
sont proches de zéro, la matrice
est numériquement singulière, d’où un échec de la
procédure, ou quasi singulière. Dans ce dernier cas, la variance asymptotique
devient excessivement élevée et perd donc toute fiabilité. Cela étant dit, la
méthode AA serait uniquement envisageable pour le modèle 4. Comme on
pouvait s’y attendre, la méthode donne de piètres résultats avec de courtes
séries et laisse des biais positifs d’environ 15 %. Le rendement pour
et
est comparable à celui de la méthode bootstrap PT1,
mais demeure significativement inférieur à celui de la méthode PT2.
3. Comme
on peut immédiatement l’observer, l’emploi du bootstrap RR crée un biais
négatif contrairement au bootstrap PT qui engendre un biais positif. À
l’encontre de l’affirmation faite par Rodriguez et Ruiz (2012) que leur méthode
offre de meilleures propriétés d’échantillon fini que la méthode de Pfeffermann et Tiller (2005), nous pouvons voir dans le cas de l’EPA que les
estimations EQM par le bootstrap RR paramétrique ou non créent des biais
négatifs plus importants que les estimations EQM par filtre de Kalman à
l’échelle des modèles et des longueurs de séries (sauf pour RR2 dans le modèle 4
quand
et dans le modèle 1 quand
et
Alors que Pfeffermann et Tiller (2005) démontrent
que leur méthode bootstrap présente des propriétés asymptotiques
satisfaisantes, Rodriguez et Ruiz (2012) illustrent la supériorité de leur
méthode dans de petits échantillons avec un modèle simple (à marche aléatoire
et à bruit). La présente étude par simulation révèle que le bootstrap RR
pourrait mal se comporter dans des applications plus complexes. Les méthodes PT
n’ont jamais créé de biais négatifs pour l’EPA, ce qui en établit la
« prudence » (sauf pour le bootstrap PT2 dans le modèle 4 quand
où le biais négatif demeure inférieur à celui de
l’application du filtre de Kalman). Un autre résultat frappant pour
est que le biais positif du bootstrap PT2 et le biais
négatif du bootstrap RR prennent des valeurs très élevées dans le
modèle 3. Il reste que, avec une série si courte et autant de composantes
non stationnaires comme dans le modèle de l’EPA, il est difficile de tirer des
estimations fiables des méthodes bootstrap non paramétriques, puisque la
période d’initialisation (avec son échantillon diffus) nécessaire à la
production non paramétrique d’une série prend plus du quart de sa durée
(13 mois sur 48).
4. Pour
les séries de longueur
et
les biais positifs engendrés par la méthode PT2
dépassent légèrement les biais FK en valeur absolue dans les modèles comportant
des hyperparamètres non significatifs (modèles 1 et 2). Dans les modèles
plus stables (modèles 3 et 4), les biais positifs sont inférieurs aux
biais négatifs FK en valeur absolue. Pour
nous présentons les résultats bootstrap seulement pour
les modèles 3 et 4 (nous ne tenons pas compte des modèles 1 et 2 qui
tendent à la surspécification à cause de problèmes numériques). Comme on
pouvait s’y attendre, les biais sont plus importants pour une telle durée des
séries : les biais négatifs FK et RR s’accroissent en valeur absolue, tout
comme les biais positifs PT, sauf pour le résultat PT2 précité dans le modèle 4.
L’EQM du signal dans le modèle 3, que
nous pourrions considérer comme un meilleur choix pour la production des
chiffres officiels de l’EPA, est estimée au mieux par la méthode PT2 avec des
biais relatifs de 1,4 % et 1,9 % respectivement pour
et
Le bootstrap PT2 serait aussi la meilleure
méthode pour
mais comme nous l’avons fait observer, les
biais négatifs FK sont déjà des plus modestes pour des séries de cette longueur.
Dans le cas de séries très courtes comme
le bootstrap PT1 paramétrique serait le
meilleur.
5. Pour
les méthodes PT et RR à la fois (sauf pour RR2 dans le modèle 4 avec
les valeurs absolues des biais relatifs sont moindres
dans le cas des méthodes non paramétriques par rapport aux méthodes
paramétriques. La supériorité du bootstrap non paramétrique peut s’expliquer
par une distorsion de la normalité de la distribution des erreurs dans les
modèles. Ainsi, notre préférence devrait aller aux bootstraps non paramétriques
sauf pour des séries chronologiques très courtes.
6. Il
n’y a pas que le biais des estimateurs EQM, puisque leur variabilité nous
éclaire grandement aussi sur leur fiabilité. Autant que nous sachions, cet
aspect n’a pas encore été exposé dans les études statistiques. Les
tableaux 5.6 et 5.7 présentent les variances et les EQM des quatre
estimateurs EQM bootstrap pour le signal, la tendance et la composante
saisonnière dans le cas des longueurs de série les plus intéressantes, à savoir
et
(nous ne tenons pas compte des modèles 1 et
2, ni de l’approximation asymptotique en raison des problèmes numériques déjà
évoqués). Les EQM des deux estimateurs EQM PT sont
plus élevées que celles des deux estimateurs EQM RR tant pour le modèle 3
que pour le modèle 4. Si ces derniers semblent d’un rendement supérieur,
comme en témoigneraient leurs EQM moindres, c’est que leurs variances sont plus
petites. Toutefois, les biais sont parfois assez élevés pour porter les EQM de
ces estimateurs EQM presque au niveau des EQM des estimateurs PT. Plus
important encore, les biais des estimateurs EQM RR sont le plus souvent
négatifs et dépassent fréquemment ceux des estimateurs par filtre de Kalman. Ce
phénomène rend les bootstraps RR difficilement applicables dans le cas qui nous
occupe.
Outre les résultats de
simulation déjà mentionnés, il est également intéressant de voir si les modèles
de séries chronologiques structurels (SCS) continuent d’offrir des estimations plus précises que les estimations de variance fondées sur le plan, même après correction de l’incertitude des
hyperparamètres. C’est pourquoi nous mettons en comparaison les racines des EQM
(REQM) obtenues avec les différentes procédures d’estimation EQM pour la série
initiale
d’une part, et les erreurs-types (ET) de
l’estimateur ERG. De telles différences moyennes des erreurs-types (DMET) dans le modèle
des séries chronologiques
se définissent ainsi :
Elles sont présentées au tableau 5.8,
étant l’estimation filtrée du paramètre réel
de population défini comme la tendance et la composante saisonnière dans le
modèle
Nous décrivons les résultats pour le filtre de
Kalman (FK) quand nous négligeons l’incertitude des hyperparamètres, ainsi que
dans les cas où les cinq méthodes d’estimation EQM sont appliquées dans une
prise en compte de cette même incertitude. Nous comparons aussi les REQM
réelles en (4.2) aux erreurs-types ERG (« Réel » en ligne au
tableau 5.8). À noter que le BRE et, en particulier, les estimations
saisonnières des hyperparamètres par l’ensemble de données initial de l’EPA
sont plutôt petits. Il n’y a donc pas de différences dignes de mention entre
les estimations ponctuelles du signal dans les quatre modèles. La méthode AA,
la moins sûre, produit des erreurs-types surestimées (par rapport à la
diminution de 18 % à 20 % pour les REQM réelles) à cause des matrices
d’information quasi singulières des estimations de maximum de vraisemblance des
hyperparamètres. Vu ce phénomène, on devrait se sentir plus en confiance dans
l’utilisation des estimateurs PT. Bien que notre étude par simulation indique
que le bootstrap PT2 est normalement d’un meilleur rendement que le bootstrap
paramétrique PT1, pour cette série en particulier les ET dégagées par le
bootstrap PT1 sont les plus proches des REMQ réelles avec une diminution
d’environ 20 % des erreurs-types de l’estimation ERG. Ainsi, la
modélisation permet une baisse significative de la variance comparativement à
une approche plus classique fondée sur le plan, et ce, même après avoir pris en
compte l’incertitude des hyperparamètres.
Tableau 5.8
Différences moyennes en pourcentage des erreurs-types (DMET) entre les estimateurs par la régression généralisée et les estimateurs de modélisation pour la série initiale de l’EPA,
augmentation en pourcentage des ET par filtre de Kalman après application de la correction EQM (entre parenthèses)
Sommaire du tableau
Le tableau montre les résultats de Différences moyennes en pourcentage des erreurs-types (DMET) entre les estimateurs par la régression généralisée et les estimateurs de modélisation pour la série initiale de l’EPA. Les données sont présentées selon (titres de rangée) et Modèle 1, Modèle 2 , Modèle 3 et Modèle 4(figurant comme en-tête de colonne).
|
Modèle 1 |
Modèle 2 |
Modèle 3 |
Modèle 4 |
| FK |
-24,1 |
-24,1 |
-24,5 |
-24,5 |
| Valeur réelle |
-20,0 (5,56) |
-20,1 (5,5) |
-20,6 (5,4) |
-20,7 (5,3) |
| AA |
-18,8 (6,9) |
-19,0 (6,7) |
-19,1 (7,1) |
-19,5 (6,6) |
| PT1 |
-20,1 (5,2) |
-20,1 (5,2) |
-21,1 (4,6) |
-21,2 (4,4) |
| PT2 |
-22,9 (1,6) |
-21,2 (3,8) |
-22,2 (3,1) |
-22,5 (2,6) |
| RR1 |
-26,5 (-3,2) |
-26,6 (-3,4) |
-26,5 (-2,7) |
-26,5 (-2,7) |
| RR2 |
-24,0 (-0,1) |
-25,4 (-1,8) |
-25,6 (-1,4) |
-25,7 (-1,6) |
ISSN : 1712-5685
Politique de rédaction
Techniques d’enquête publie des articles sur les divers aspects des méthodes statistiques qui intéressent un organisme statistique comme, par exemple, les problèmes de conception découlant de contraintes d’ordre pratique, l’utilisation de différentes sources de données et de méthodes de collecte, les erreurs dans les enquêtes, l’évaluation des enquêtes, la recherche sur les méthodes d’enquête, l’analyse des séries chronologiques, la désaisonnalisation, les études démographiques, l’intégration de données statistiques, les méthodes d’estimation et d’analyse de données et le développement de systèmes généralisés. Une importance particulière est accordée à l’élaboration et à l’évaluation de méthodes qui ont été utilisées pour la collecte de données ou appliquées à des données réelles. Tous les articles seront soumis à une critique, mais les auteurs demeurent responsables du contenu de leur texte et les opinions émises dans la revue ne sont pas nécessairement celles du comité de rédaction ni de Statistique Canada.
Présentation de textes pour la revue
Techniques d’enquête est publiée en version électronique deux fois l’an. Les auteurs désirant faire paraître un article sont invités à le faire parvenir en français ou en anglais en format électronique et préférablement en Word au rédacteur en chef, (statcan.smj-rte.statcan@canada.ca, Statistique Canada, 150 Promenade du Pré Tunney, Ottawa, (Ontario), Canada, K1A 0T6). Pour les instructions sur le format, veuillez consulter les directives présentées dans la revue ou sur le site web (www.statcan.gc.ca/Techniquesdenquete).
Note de reconnaissance
Le succès du système statistique du Canada repose sur un partenariat bien établi entre Statistique Canada et la population, les entreprises, les administrations canadiennes et les autres organismes. Sans cette collaboration et cette bonne volonté, il serait impossible de produire des statistiques précises et actuelles.
Normes de service à la clientèle
Statistique Canada s'engage à fournir à ses clients des services rapides, fiables et courtois. À cet égard, notre organisme s'est doté de normes de service à la clientèle qui doivent être observées par les employés lorsqu'ils offrent des services à la clientèle.
Droit d'auteur
Publication autorisée par le ministre responsable de Statistique Canada.
© Ministre de l'Industrie, 2017
L'utilisation de la présente publication est assujettie aux modalités de l'Entente de licence ouverte de Statistique Canada.
N° 12-001-X au catalogue
Périodicité : Semi-annuel
Ottawa



