La modélisation espace-état appliquée aux séries chronologiques de l’Enquête sur la population active des Pays-Bas : sélection de modèles et estimation de l’erreur quadratique moyenne
Section 6. Observations en conclusion

Table des matières

Les organismes nationaux de statistique s’intéressent de plus en plus à l’utilisation de modèles de séries chronologiques structurels (SCS) pour la production des chiffres mensuels de la population active. Aux Pays-Bas, un tel modèle est appliqué depuis 2010. Le modèle SCS représente une sorte d’estimation sur petits domaines (EPD) où l’information tirée d’échantillons de périodes antérieures permet d’obtenir des estimations plus précises, et de tenir compte du plan de sondage avec renouvellement de panel, lequel est souvent employé dans les enquêtes sur la population active.

Si l’on ne tient pas compte de l’incertitude des hyperparamètres dans les EQM des estimations fondées sur des modèles SCS, on se trouve à sous-estimer les EQM des estimations de domaines. Le biais qui se crée lorsqu’on écarte ainsi l’incertitude des hyperparamètres peut être important, plus particulièrement quand les séries sont courtes, ce qui est souvent le cas dans les organismes nationaux de statistique. La plupart des applications des procédures EPD dans les études spécialisées reposent sur des modèles multiniveaux, pratique courante lorsqu’il s’agit de tenir compte de l’incertitude des hyperparamètres. Les études consacrées au modèles SCS dans le contexte des estimations sur petits domaines sont plutôt limitées et la plupart des applications ne tiennent pas compte de cette incertitude dans les estimations EQM. L’importance du biais dans les EQM obtenues dépend de la structure du modèle et de la longueur de la série. Le présent article décrit une simulation de Monte-Carlo appliquée au modèle SCS qu’utilise Statistics Netherlands pour estimer le chômage mensuel. Cette simulation a un double but. D’abord, elle établit la quantité de biais dans les EQM de l’EPA quand on néglige l’incertitude des hyperparamètres. De plus, nous comparons notre simulation à plusieurs méthodes d’estimation EQM disponibles dans la documentation spécialisée pour le cadre de modèles SCS et établissons ainsi la meilleure méthode pour l’EPA des Pays-Bas. En deuxième lieu, nous jugeons que la simulation des distributions des estimateurs des hyperparamètres permet de mieux comprendre la dynamique des composantes inobservées de le modèle SCS et donc de vérifier la nécessité de modéliser les composantes comme variant dans le temps. Dans le cas de l’EPA, la simulation fait voir l’intérêt éventuel d’adopter une version plus restreinte du modèle où le biais de renouvellement de l’échantillon serait invariant dans le temps et où le bruit blanc de population serait négligé. Pour cette double raison, nous recommandons d’effectuer une simulation comme celle que nous décrivons dans le processus de mise en œuvre du modèle servant à la production des statistiques officielles.

La comparaison des méthodes d’estimation EQM jette en outre un nouvel éclairage sur leurs propriétés. L’approximation asymptotique est inapplicable aux cas où les hyperparamètres sont proches de zéro, parce que la matrice d’information des estimations des hyperparamètres devient (presque) singulière. Les bootstraps non paramétriques, parce qu’ils dépendent moins d’hypothèses de normalité, sont d’un meilleur rendement que les bootstraps paramétriques selon Pfeffermann et Tailler (2005) et Rodriguez et Ruiz (2012) à la fois sauf si les séries sont très courtes. Notre constatation première est que les bootstraps PT présentent des biais positifs et sont invariablement d’un rendement supérieur à celui des bootstraps RR dont les biais sont généralement négatifs et plus importants (en valeur absolue) que dans l’application du filtre de Kalman. Elle contredit Rodriguez et Ruiz (2012) qui affirment la supériorité de leur méthode lorsque les séries chronologiques sont courtes. On peut penser que leurs résultats sont purement heuristiques, étant fondés sur un modèle simple (marche aléatoire et bruit), alors que Pfeffermann et Tiller (2005) démontrent que leur méthode bootstrap produit des estimations EQM avec un biais d’un bon ordre.

Les variances des estimateurs EQM PT sont plus élevées que celles des estimateurs RR correspondants. Les différences entre ces deux types d’estimateurs varient de modestes à modérées (les EQM des seconds sont inférieures de 28 % à 8 % aux EQM des premiers selon le modèle et la longueur de la série). Aspect plus important encore, la tendance des estimateurs RR à engendrer des biais négatifs parfois supérieurs à ceux de l’application du filtre de Kalman rend inapplicables ces méthodes bootstrap. Ainsi, on devrait généralement envisager de recourir aux méthodes PT pour d’autres données d’enquête, quoique leur rendement le cède occasionnellement à celui des méthodes RR.

Dans le cas des séries chronologiques très courtes, les bootstraps non paramétriques ne seraient pas un choix possible pour un modèle qui aurait la complexité que nous présentons. Il reste que le bootstrap paramétrique PT corrige les EQM aux biais négatifs jusqu’à dégager un léger biais positif (de 1,4 % à 4,4 % selon le modèle). Pour la présente durée de série de 114 mois, il est possible d’abaisser de -2,4 % à 1,9 % le biais EQM négatif grâce à la méthode non paramétrique de Pfeffermann et Tiller (2005) dans le modèle où le BRE est invariant dans le temps. Les racines des EQM réelles par filtre de Kalman sont inférieures d’environ 20 % aux erreurs-types des estimations ERG dans les quatre modèles appliqués aux données de l’EPA. En général, les biais des estimations EQM par filtre de Kalman sont relativement modestes dans l’application de l’EPA, aussi parraîtrait-il suffisant de s’en remettre à ces estimations naïves pour la publication des chiffres officiels.

Remerciements

Nous remercions Statistics Netherlands d’avoir financé cette étude. Nous remercions également le rédacteur adjoint et les examinateurs anonymes d’avoir lu attentivement notre manuscrit et formulé de précieuses observations. Les points de vue exprimés dans la présente sont ceux des auteurs et ne reflètent pas nécessairement les politiques de Statistics Netherlands.

Annexes

A. Densités simulées des hyperparamètres dans les quatre versions du modèle de l’EPA

Nous présentons en annexe les fonctions de densité des hyperparamètres obtenues par simulation quand les quatre versions du modèle de l’EPA (voir le tableau 5.1) servent de processus de génération de données. L’axe des x présente les hyperparamètres de variance à l’échelle logarithmique et l’axe des y porte les valeurs de fréquence. L’axe des x peut être étiré à cause des valeurs aberrantes.

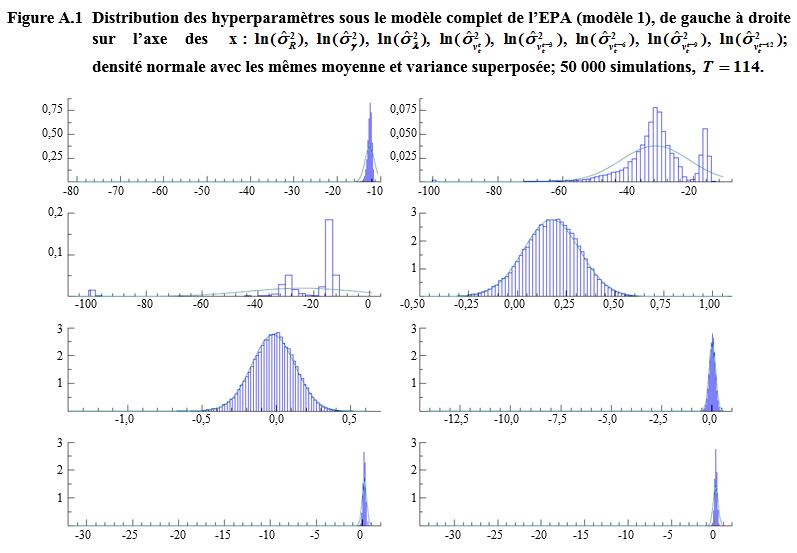
Figure A.1

Description de la figure A.1

Figure présentant les distributions des hyperparamètres sous le modèle complet de l’EPA (modèle 1) pour huit hyperparamètres de variance soient ${\hat{σ}}_{R}^{2},$ ${\hat{σ}}_{γ}^{2},$ ${\hat{σ}}_{λ}^{2},$ ${\hat{σ}}_{v_{t}^{t}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2} .$ La fonction de densité normale avec les mêmes moyennes et variances est superposées sur chaque graphique. L’axe des x présente les hyperparamètres de variance à l’échelle logarithmique et l’axe des y porte les valeurs de fréquence. L’axe des x peut être étiré à cause des valeurs aberrantes.

Pour ${\hat{σ}}_{R}^{2},$ l’axe des x va de -80 à -10 et l’axe des y va de 0 à 0,75. Les valeurs sont très concentrées autour de la moyenne formant un pic et dépassent la normale.

Pour ${\hat{σ}}_{γ}^{2},$ l’axe des x va de -100 à -10 et l’axe des y va de 0 à 0,075. Il y a des valeurs aberrantes à gauche. La distribution est bimodale.

Pour ${\hat{σ}}_{λ}^{2},$ l’axe des x va de -100 à 0 et l’axe des y va de 0 à 0,2. Il y a des valeurs aberrantes à gauche. La distribution est bimodale et très aplatie.

Pour ${\hat{σ}}_{v_{t}^{t}}^{2},$ l’axe des x va de -0,5 à 0,75 et l’axe des y va de 0 à 3. La distribution semble proche de la normale.

Pour ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ l’axe des x va de -1,0 à 0,5 et l’axe des y va de 0 à 3. La distribution semble proche de la normale.

Pour ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ l’axe des x va de -12,5 à 1,0 et l’axe des y va de 0 à 3. Les valeurs sont très concentrées autour de la moyenne formant un petit pic.

Pour ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2},$ les axes des x vont de -30 à 2 et les axes des y vont de 0 à 3. Les valeurs sont concentrées autour de la moyenne formant un pic et dépassent la normale.

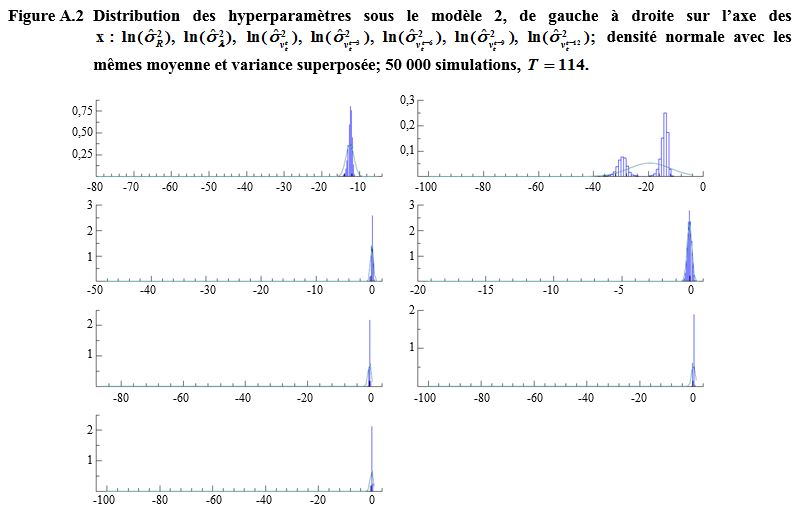
Figure A.2

Description de la figure A.2

Figure présentant les distributions des hyperparamètres sous le modèle complet de l’EPA (modèle 2) pour sept hyperparamètres de variance soient ${\hat{σ}}_{R}^{2},$ ${\hat{σ}}_{λ}^{2},$ ${\hat{σ}}_{v_{t}^{t}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2} .$ La fonction de densité normale avec les mêmes moyennes et variances est superposées sur chaque graphique. L’axe des x présente les hyperparamètres de variance à l’échelle logarithmique et l’axe des y porte les valeurs de fréquence. L’axe des x peut être étiré à cause des valeurs aberrantes.

Pour ${\hat{σ}}_{R}^{2},$ l’axe des x va de -80 à -10 et l’axe des y va de 0 à 0,75. Les valeurs sont très concentrées autour de la moyenne formant un pic et dépassent la normale.

Pour ${\hat{σ}}_{λ}^{2},$ l’axe des x va de -100 à 0 et l’axe des y va de 0 à 0,3. La distribution est bimodale et la courbe normale est très aplatie.

Pour ${\hat{σ}}_{v_{t}^{t}}^{2},$ l’axe des x va de -50 à 2 et l’axe des y va de 0 à 3. Les valeurs sont très concentrées autour de la moyenne formant un haut pic et dépassent la normale.

Pour ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ l’axe des x va de -20 à 1 et l’axe des y va de 0 à 3. Les valeurs sont concentrées autour de la moyenne formant un pic.

Pour ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ l’axe des x va de -80 à 0 et l’axe des y va de 0 à 2. Les valeurs sont très concentrées autour de la moyenne formant un haut pic et dépassent la normale.

Pour ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2},$ les axes des x vont de -100 à 0 et les axes des y vont de 0 à 2. Les valeurs sont concentrées autour de la moyenne formant un haut pic et dépassent la normale.

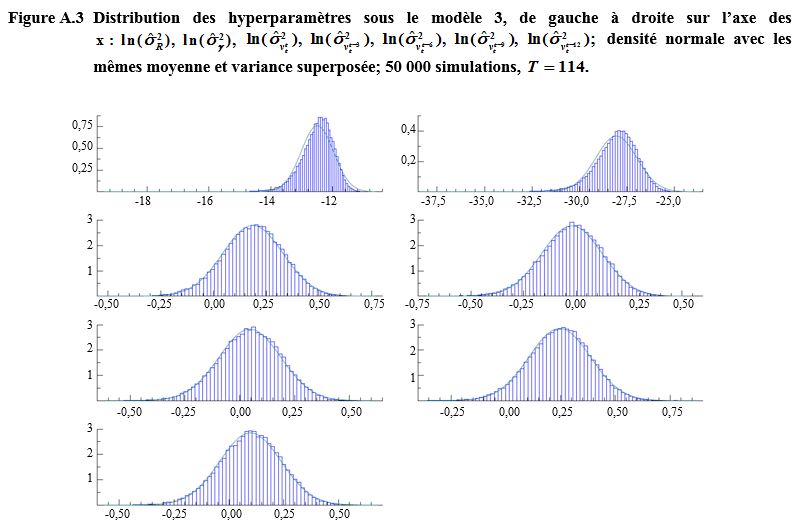
Figure A.3

Description de la figure A.3

Figure présentant les distributions des hyperparamètres sous le modèle complet de l’EPA (modèle 3) pour sept hyperparamètres de variance soient ${\hat{σ}}_{R}^{2},$ ${\hat{σ}}_{γ}^{2},$ ${\hat{σ}}_{v_{t}^{t}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2} .$ La fonction de densité normale avec les mêmes moyennes et variances est superposées sur chaque graphique. L’axe des x présente les hyperparamètres de variance à l’échelle logarithmique et l’axe des y porte les valeurs de fréquence.

Pour ${\hat{σ}}_{R}^{2},$ l’axe des x va de -18 à -10 et l’axe des y va de 0 à 0,75. Les valeurs sont concentrées autour de la moyenne et asymétriques, mais proches de la courbe normale.

Pour ${\hat{σ}}_{γ}^{2},$ l’axe des x va de -37,5 à -25 et l’axe des y va de 0 à 0,3. Les valeurs sont concentrées autour de la moyenne et asymétriques, mais proches de la courbe normale.

Pour ${\hat{σ}}_{v_{t}^{t}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2},$ les axes des x vont de -0,50 à 0,50 et les axes des y vont de 0 à 3. Les valeurs sont très proches de la courbe normale.

Pour ${\hat{σ}}_{v_{t}^{t - 9}}^{2},$ l’axe des x va de -0,25 à 0,75 et l’axe des y va de 0 à 3. Les valeurs sont très proches de la courbe normale.

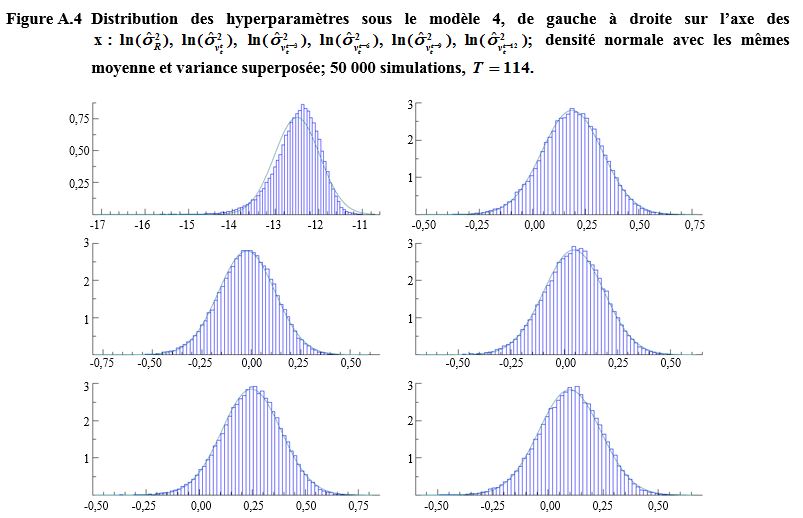
Figure A.4

Description de la figure A.4

Figure présentant les distributions des hyperparamètres sous le modèle complet de l’EPA (modèle 4) pour six hyperparamètres de variance soient ${\hat{σ}}_{R}^{2},$ ${\hat{σ}}_{v_{t}^{t}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 9}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2} .$ La fonction de densité normale avec les mêmes moyennes et variances est superposées sur chaque graphique. L’axe des x présente les hyperparamètres de variance à l’échelle logarithmique et l’axe des y porte les valeurs de fréquence.

Pour ${\hat{σ}}_{R}^{2},$ l’axe des x va de -17 à -11 et l’axe des y va de 0 à 0,75. Les valeurs sont concentrées autour de la moyenne et asymétriques, mais proches de la courbe normale.

Pour ${\hat{σ}}_{v_{t}^{t}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 9}}^{2},$ les axes des x vont de -0,25 à 0,75 et les axes des y vont de 0 à 3. Les valeurs sont très proches de la courbe normale.

Pour ${\hat{σ}}_{v_{t}^{t - 3}}^{2},$ ${\hat{σ}}_{v_{t}^{t - 6}}^{2}$ et ${\hat{σ}}_{v_{t}^{t - 12}}^{2},$ l’axe des x va de -0,50 à 0,50 et l’axe des y va de 0 à 3. Les valeurs sont très proches de la courbe normale.

B. Rendement prévisionnel des quatre modèles de l’EPA

Tableau B.1
Racine des écarts quadratiques moyens des estimations par la régression généralisée du nombre de chômeurs par prédiction « un pas avant » et par vague
Sommaire du tableau
Le tableau montre les résultats de Racine des écarts quadratiques moyens des estimations par la régression généralisée du nombre de chômeurs par prédiction « un pas avant » et par vague . Les données sont présentées selon Vague (titres de rangée) et Modèle 1, Modèle 2, Modèle 3 et Modèle 4(figurant comme en-tête de colonne).
Vague	Modèle 1			Modèle 2			Modèle 3			Modèle 4
Vague	$d =20$	$d =30$	$d =60$	$d =20$	$d =30$	$d =60$	$d =20$	$d =30$	$d =60$	$d =20$	$d =30$	$d =60$
1	34 370	33 582	34 641	34 370	33 582	34 641	34 518	33 754	34 881	34 525	33 757	34 885
2	30 130	29 770	29 410	30 130	29 770	29 410	30 138	29 780	29 418	30 144	29 779	29 409
3	35 792	32 631	34 654	35 792	32 631	34 654	35 714	32 535	34 499	35 716	32 532	34 499
4	39 647	38 556	36 797	39 647	38 556	36 797	39 753	38 640	36 891	39 743	38 633	36 889
5	38 271	37 622	36 341	38 271	37 622	36 341	38 183	37 528	36 225	38 177	37 523	36 226

Bibliographie

Bailar, B. (1975). The effects of rotation group bias on estimates from panel surveys. Journal of the American Statistical Association, 70, 23-30.

Bartlett, M.S. (1946). On the theoretical specification and sampling properties of autocorrelated time-series. Supplement to the Journal of the Royal Statistical Society, 8, 27-41.

Binder, D.A., et Dick, J.P. (1990). Méthode pour l’analyse des modèles ARMMI. Techniques d’enquête, 16, 2, 251-265. Article accessible à l’adresse http://www.statcan.gc.ca/pub/12-001-x/1990002/article/14533-fra.pdf.

Bollineni-Balabay, O., van den Brakel, J. et Palm, F. (2016a). Multivariate state space approach to variance reduction in series with level and variance breaks due to survey redesigns. Journal of the Royal Statistical Society: Series A (Statistics in Society), 179, 377-402.

Bollineni-Balabay, O., van den Brakel, J. et Palm, F. (2016b). State space time series modelling of the Dutch Labour Force Survey: Model selection and MSE estimation, - Extended version. Document de travail, Statistics Netherlands, Heerlen. https://www.cbs.nl/en-gb/background/2016/41/state-space-time-series.

Cochran, W. (1977). Sampling Techniques. New York: John Wiley & Sons, Inc.

Doornik, J. (2007). An Object-Oriented Matrix Programming Language Ox 5. Timberlake Consultants Press, Londres.

Durbin, J., et Koopman, S.J. (2002). A simple and efficient simulation smoother for state space time series analysis. Biometrika, 89, 603-615.

Durbin, J., et Koopman, S.J. (2012). Time Series Analysis by State Space Methods. Numéro 38. Oxford University Press.

EUROSTAT (2015). Task force on monthly unemployment - revised report. Working group labour market statistics.

Hamilton, J. (1986). A standard error for the estimated state vector of a state-space model. Journal of Econometrics, 33, 387-397.

Harvey, A. (1989). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press, Cambridge.

Koopman, S.J. (1997). Exact initial kalman filtering and smoothing for nonstationary time series models. Journal of the American Statistical Association, 92, 1630-1638.

Koopman, S.J., Shephard, N. et Doornik, J. (2008). SsfPack 3.0: Statistical Algorithms for Models in State Space Form. Timberlake Consultants Press, Londres.

Krieg, S., et van den Brakel, J. (2012). Estimation of the monthly unemployment rate for six domains through structural time series modelling with cointegrated trends. Computational Statistics & Data Analysis, 56, 2918-2933.

Lemaître, G., et Dufour, J. (1987). Une méthode intégrée de pondération des personnes et des familles. Techniques d’enquête, 13, 2, 211-220. Article accessible à l’adresse http://www.statcan.gc.ca/pub/12-001-x/1987002/article/14607-fra.pdf.

ONS (2015). A state space model for LFS estimates: Agreeing the target and dealing with wave specific bias. Rapport de la 29^e réunion du Comité consultatif de la méthodologie des services statistiques du gouvernement. http://www.ons.gov.uk/ons/guide-method/method-quality/advisory-committee/previous-meeting-papers-and-minutes/mac-29-papers.pdf.

Pfeffermann, D. (1991). Estimation and seasonal adjustment of population means using data from repeated surveys. Journal of Business and Economic Statistics, 9, 163-175.

Pfeffermann, D. (2013). New important developments in small area estimation. Statistical Science, 28, 40-68.

Pfeffermann, D., et Rubin-Bleuer, S. (1993). Modélisation conjointe robuste de séries de données sur l’activité pour de petites régions. Techniques d’enquête, 19, 2, 159-174. Article accessible à l’adresse http://www.statcan.gc.ca/pub/12-001-x/1993002/article/14458-fra.pdf.

Pfeffermann, D., et Tiller, R. (2005). Bootstrap approximation to prediction MSE for state-space models with estimated parameters. Journal of Time Series Analysis, 26, 893-916.

Pfeffermann, D., Feder, M. et Signorelli, D. (1998). Estimation of autocorrelations of survey errors with application to trend estimation in small areas. Journal of Business and Economic Statistics, 16, 339-348.

Rao, J.N.K., et Molina, I. (2015). Small Area Estimation. New York: John Wiley & Sons, Inc.

Rodriguez, A., et Ruiz, E. (2012). Bootstrap prediction mean squared errors of unobserved states based on the Kalman filter with estimated parameters. Computational Statistics and Data Analysis, 56, 62-74.

Särndal, C.-E., Swensson, B. et Wretman, J. (1992). Model Assisted Survey Sampling. Springer.

Tiller, R. (1992). Time series modelling of sample survey data from the US current population survey. Journal of Official Statistics, 8, 149-166.

van den Brakel, J., et Krieg, S. (2009). Estimation du taux de chômage mensuel par modélisation structurelle de séries chronologiques dans un plan de sondage avec renouvellement de panel. Techniques d’enquête, 35, 2, 193-207. Article accessible à l’adresse http://www.statcan.gc.ca/pub/12-001-x/2009002/article/11040-fra.pdf.

van den Brakel, J., et Krieg, S. (2015). Remédier aux petites tailles d’échantillon, au biais de groupe de renouvellement et aux discontinuités dans les plans de sondage avec renouvellement de panel. Techniques d’enquête, 41, 2, 281-312. Article accessible à l’adresse http://www.statcan.gc.ca/pub/12-001-x/2015002/article/14231-fra.pdf.

Zhang, M., et Honchar, O. (2016). Predicting survey estimates by state space models using multiple data sources. Article pour le Comité consultatif de la méthodologie de l’Australian Bureau of Statistics.

ISSN : 1712-5685

Politique de rédaction

Techniques d’enquête publie des articles sur les divers aspects des méthodes statistiques qui intéressent un organisme statistique comme, par exemple, les problèmes de conception découlant de contraintes d’ordre pratique, l’utilisation de différentes sources de données et de méthodes de collecte, les erreurs dans les enquêtes, l’évaluation des enquêtes, la recherche sur les méthodes d’enquête, l’analyse des séries chronologiques, la désaisonnalisation, les études démographiques, l’intégration de données statistiques, les méthodes d’estimation et d’analyse de données et le développement de systèmes généralisés. Une importance particulière est accordée à l’élaboration et à l’évaluation de méthodes qui ont été utilisées pour la collecte de données ou appliquées à des données réelles. Tous les articles seront soumis à une critique, mais les auteurs demeurent responsables du contenu de leur texte et les opinions émises dans la revue ne sont pas nécessairement celles du comité de rédaction ni de Statistique Canada.

Présentation de textes pour la revue

Techniques d’enquête est publiée en version électronique deux fois l’an. Les auteurs désirant faire paraître un article sont invités à le faire parvenir en français ou en anglais en format électronique et préférablement en Word au rédacteur en chef, (statcan.smj-rte.statcan@canada.ca, Statistique Canada, 150 Promenade du Pré Tunney, Ottawa, (Ontario), Canada, K1A 0T6). Pour les instructions sur le format, veuillez consulter les directives présentées dans la revue ou sur le site web (www.statcan.gc.ca/Techniquesdenquete).

Note de reconnaissance

Le succès du système statistique du Canada repose sur un partenariat bien établi entre Statistique Canada et la population, les entreprises, les administrations canadiennes et les autres organismes. Sans cette collaboration et cette bonne volonté, il serait impossible de produire des statistiques précises et actuelles.

Normes de service à la clientèle

Statistique Canada s'engage à fournir à ses clients des services rapides, fiables et courtois. À cet égard, notre organisme s'est doté de normes de service à la clientèle qui doivent être observées par les employés lorsqu'ils offrent des services à la clientèle.

Droit d'auteur

Publication autorisée par le ministre responsable de Statistique Canada.

L'utilisation de la présente publication est assujettie aux modalités de l'Entente de licence ouverte de Statistique Canada.

N° 12-001-X au catalogue

Périodicité : Semi-annuel

Ottawa

Date de modification :: 2017-06-22

Sélection de la langue

Recherche et menus

Recherche

La modélisation espace-état appliquée aux séries chronologiques de l’Enquête sur la population active des Pays-Bas : sélection de modèles et estimation de l’erreur quadratique moyenne
Section 6. Observations en conclusion

Remerciements

Annexes

A. Densités simulées des hyperparamètres dans les quatre versions du modèle de l’EPA

B. Rendement prévisionnel des quatre modèles de l’EPA

Bibliographie

La modélisation espace-état appliquée aux séries chronologiques de l’Enquête sur la population active des Pays-Bas : sélection de modèles et estimation de l’erreur quadratique moyenne Section 6. Observations en conclusion

Remerciements

Annexes

A. Densités simulées des hyperparamètres dans les quatre versions du modèle de l’EPA

B. Rendement prévisionnel des quatre modèles de l’EPA

Bibliographie

Politique de rédaction

Présentation de textes pour la revue

Note de reconnaissance

Normes de service à la clientèle

Droit d'auteur

La modélisation espace-état appliquée aux séries chronologiques de l’Enquête sur la population active des Pays-Bas : sélection de modèles et estimation de l’erreur quadratique moyenne
Section 6. Observations en conclusion