Inférence bayésienne prédictive sur une proportion sous un modèle double pour petits domaines avec corrélations hétérogènes
Section 3. Étude numérique et comparaisons
À la présente section, nous procédons à
des études empiriques pour évaluer la performance du modèle CHE que nous comparons au modèle CHO. À la section 3.1, nous donnons un
exemple et à la section 3.2, nous présentons une étude en simulation.
3.1 Un exemple
Nous utilisons des données recueillies
auprès de la population d’élèves de troisième année aux États-Unis; voir Nandram (2015) pour une brève discussion de ces
données. L’ensemble de données, recueilli en 1999, a trait
à 2 477 élèves qui ont participé à la Third International Mathematics and Science Study (TIMSS). Foy,
Rust, et Schleicher (1996) ont décrit le plan d’échantillonnage systématique avec
probabilité proportionnelle à la taille (PPT) utilisé pour la collecte des
données de la TIMSS, et Caslyn, Gonzales
et Frase (1999) ont présenté les faits saillants de l’enquête. Les domaines
sont formés en recoupant quatre régions (nord-est, sud, centre et ouest) et
trois types de collectivité des États-Unis (village ou région rurale, périphérie
d’une ville, et proximité du centre d’une ville). Donc, il y a douze domaines.
La variable binaire est la question de savoir si la note de mathématique de
l’élève est ou non inférieure à la moyenne. Les grappes sont les écoles, tandis
que les unités dans les grappes sont les élèves.
Pour évaluer la qualité de l’inférence
bayésienne prédictive, comme l’a suggéré un examinateur, Nandram (2015) a pris un échantillon correspondant
à la moitié des données originales et l’a appelé échantillon synthétique.
L’échantillon original a servi de population, et le demi-échantillon a été
utilisé pour l’analyse, ce qui a fourni une méthode pour évaluer le pouvoir
prédictif des modèles dans Nandram
(2015). Dans le présent article, comme l’a proposé un examinateur, au lieu
d’utiliser un demi-échantillon, nous nous servons de l’ensemble de données
original à notre disposition; voir le tableau 3.1 pour la description de
l’ensemble de données complet que nous analysons dans le présent article. Nous
évaluons principalement le pouvoir prédictif du modèle CHE au moyen de l’étude en simulation.
Malheureusement, comme dans le cas de nombreuses
enquêtes complexes, les analystes des données secondaires ne connaissent pas
les fractions d’échantillonnage. Cependant, pour nombre de ces enquêtes, les
fractions d’échantillonnage sont habituellement relativement faibles. Dans le
cas des données de la TIMSS, nous supposons que l’ensemble de données est un
échantillon de 5 % de la population. Par exemple, si quatre écoles
sont échantillonnées pour un domaine, disons le
domaine
le nombre total de grappes,
est supposé être 80. Si
17 élèves sont observés dans une école échantillonnée, disons la
école, le nombre total
d’élèves,
est supposé être 340. Pour
les écoles non échantillonnées,
est supposé être la moyenne
du nombre total d’élèves dans les écoles échantillonnées pour chaque domaine.
En outre, dans de nombreuses écoles, beaucoup d’élèves, voire tous, étaient
soit en dessous soit au-dessus de la moyenne. Cet ensemble de données est donc très
épars, ce qui rend l’estimation directe difficile.
Tableau 3.1
Nombre d’élèves américains sous la moyenne en mathématique dans les écoles par domaine
Sommaire du tableau
Le tableau montre les résultats de Nombre d’élèves américains sous la moyenne en mathématique dans les écoles par domaine. Les données sont présentées selon Domaine (titres de rangée) et (s, n), m et Écoles(figurant comme en-tête de colonne).
| Domaine |
(s, n) |
m |
Écoles |
| NR |
40 |
4 |
9 |
10 |
11 |
10 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 74 |
Ceci est une cellule vide |
17 |
16 |
21 |
20 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| NP |
60 |
9 |
8 |
7 |
12 |
3 |
12 |
8 |
7 |
1 |
2 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 173 |
Ceci est une cellule vide |
20 |
21 |
17 |
19 |
16 |
25 |
22 |
14 |
19 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| NC |
135 |
11 |
9 |
20 |
1 |
22 |
20 |
11 |
26 |
10 |
1 |
12 |
3 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 222 |
Ceci est une cellule vide |
15 |
23 |
16 |
25 |
22 |
25 |
27 |
19 |
16 |
22 |
12 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| SR |
84 |
8 |
6 |
14 |
14 |
9 |
14 |
10 |
12 |
5 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 140 |
Ceci est une cellule vide |
16 |
21 |
16 |
14 |
23 |
19 |
22 |
9 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| SP |
164 |
16 |
14 |
9 |
12 |
10 |
18 |
11 |
3 |
0 |
13 |
9 |
13 |
8 |
11 |
10 |
19 |
4 |
| 298 |
Ceci est une cellule vide |
19 |
14 |
13 |
18 |
22 |
18 |
21 |
16 |
18 |
15 |
26 |
9 |
19 |
22 |
25 |
23 |
| SC |
150 |
13 |
16 |
11 |
13 |
6 |
8 |
9 |
13 |
6 |
11 |
15 |
15 |
18 |
9 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 225 |
Ceci est une cellule vide |
16 |
13 |
17 |
16 |
19 |
16 |
18 |
12 |
19 |
16 |
19 |
21 |
23 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| CR |
17 |
2 |
7 |
10 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 39 |
Ceci est une cellule vide |
16 |
23 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| CP |
59 |
7 |
13 |
11 |
5 |
15 |
3 |
2 |
10 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 140 |
Ceci est une cellule vide |
22 |
18 |
9 |
19 |
24 |
23 |
25 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| CC |
145 |
14 |
21 |
1 |
12 |
9 |
12 |
13 |
16 |
13 |
7 |
12 |
7 |
8 |
4 |
10 |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 259 |
Ceci est une cellule vide |
21 |
26 |
22 |
13 |
16 |
18 |
21 |
18 |
17 |
18 |
17 |
19 |
16 |
17 |
Ceci est une cellule vide |
Ceci est une cellule vide |
| OR |
54 |
7 |
13 |
11 |
4 |
2 |
7 |
11 |
6 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 118 |
Ceci est une cellule vide |
15 |
19 |
10 |
16 |
16 |
20 |
22 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| OP |
117 |
13 |
8 |
11 |
15 |
9 |
7 |
10 |
1 |
15 |
14 |
9 |
7 |
6 |
5 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| 224 |
Ceci est une cellule vide |
13 |
13 |
25 |
16 |
20 |
12 |
20 |
18 |
20 |
17 |
17 |
17 |
16 |
Ceci est une cellule vide |
Ceci est une cellule vide |
Ceci est une cellule vide |
| OC |
331 |
31 |
9 |
17 |
10 |
12 |
15 |
15 |
8 |
22 |
20 |
7 |
18 |
7 |
13 |
15 |
13 |
8 |
|
Ceci est une cellule vide |
6 |
8 |
17 |
13 |
9 |
6 |
12 |
7 |
11 |
4 |
9 |
8 |
2 |
3 |
7 |
Ceci est une cellule vide |
| 515 |
Ceci est une cellule vide |
18 |
22 |
10 |
14 |
15 |
15 |
8 |
23 |
22 |
7 |
18 |
10 |
26 |
29 |
13 |
17 |
|
Ceci est une cellule vide |
16 |
14 |
18 |
15 |
13 |
23 |
21 |
26 |
16 |
11 |
14 |
14 |
17 |
15 |
15 |
Ceci est une cellule vide |
Nous appliquons trois procédures
d’évaluation de la qualité de l’ajustement des modèles, à savoir le critère
d’information de Déviance (DIC pour Deviance information criterion), la
valeur p prédictive a posteriori
bayésienne (BPP pour Bayesian posterior predictive
value) et le logarithme
de la pseudo-vraisemblance marginale (LPML pour Log pseudo marginal likelihood),
qui est une mesure fondée sur la même procédure de validation croisée avec
suppression d’une unité (leave-one-out). Nous pouvons évaluer l’ajustement global des
modèles au moyen de ces procédures.
Dans le modèle CHE,
Donc, en éliminant les
par intégration, nous pouvons
obtenir la fonction de masse de probabilité bêta-binomiale suivante,
Il
est également vrai que
et
Soit
et
les itérations provenant de
l’échantillonneur de Gibbs par blocs. Soit
et
En posant que
et
le critère d’information de
déviance est donné par
Les modèles dont le DIC est petit sont préférés à ceux dont le DIC
est grand. Cependant, puisque le critère DIC a tendance à sélectionner des modèles
surajustés, Nandram (2015) a décrit les
valeurs
prédictives bayésiennes comme auxiliaire. Pour le modèle CHE, la fonction de divergence est
Soient
les échantillons répétés (rep) tirés de la distribution prédictive a posteriori
de
Alors, le critère BPP est
ce qui est calculé sur ses
itérations correspondantes
Une valeur de cette probabilité
proche de 0 ou de 1 indique un mauvais ajustement du modèle. En fait,
les modèles dont le BPP est compris dans l’intervalle (0,05; 0,95) sont considérés comme étant raisonnables.
En plus de ces quantités, nous pouvons évaluer la qualité de
l’ajustement des modèles au moyen d’une autre mesure, le LPML, qui est une
statistique sommaire des valeurs de l’ordonnée prédictive conditionnelle (CPO pour Conditional predictive ordinate),
et est fondée sur une validation croisée. Contrairement au critère DIC, de
grandes valeurs du LPML indiquent un meilleur ajustement des modèles (par
exemple, Geisser et Eddy 1979).
Dans le cas du modèle CHE, le
critère CPO peut être estimé par
où
représente les échantillons tirés de
et
Notons que, pour chaque
est la moyenne harmonique des vraisemblances
Alors, le LPML est donné par
Ces trois mesures d’évaluation des modèles ont des formes similaires
sous le modèle CHO. Pour le modèle CHO (CHE),
DIC = 774,421 (773,173), BPP = 0,349 (0,408),
LPML = -352,064 (-346,171), ce qui indique que le modèle CHE donne un meilleur ajustement. À un niveau
de détail plus fin, nous avons également examiné les valeurs de CPO
individuelles provenant des deux modèles pour chaque école. À la
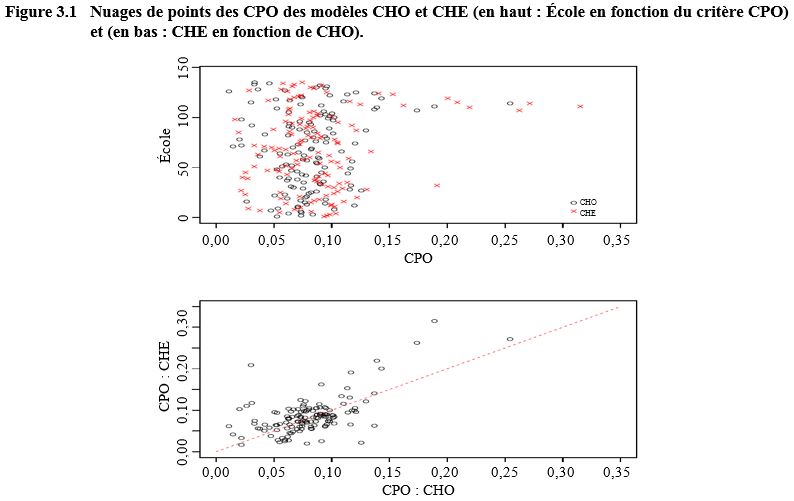
figure 3.1, nous comparons les CPO pour les modèles CHE et CHO,
et nous constatons qu’en général, les valeurs de CPO sont plus élevées pour le
modèle CHE que pour le modèle CHO. En fait, sous le modèle CHO (CHE),
nous avons constaté que le pourcentage des valeurs de CPO inférieures à 0,025
est de 3,70 % (2,96 %) et que le pourcentage des valeurs de CPO
inférieures à 0,014 est de 0,74 % (0,00 %). Ces résultats ne donnent
aucun indice d’un écart important par rapport aux hypothèses de modélisation;
voir Ntzoufras (2009). Par conséquent, à
première vue, ces mesures donnent des preuves que le modèle CHE est un peu mieux ajusté aux données de la
TIMSS que le modèle CHO.
Description de la figure 3.1
Figure composée de deux graphiques en nuage de points. Le premier compare les valeurs de CPO individuelles provenant des modèles CHE et CHO pour chaque école. L’école est sur l’axe des y, allant de 0 à 150. Les CPO sont sur l’axe des x, allant de 0,00 à 0,35. La grande majorité des points se concentre entre des valeurs de CPO de 0,00 et de 0,15 pour les deux modèles.
Le deuxième graphique compare les CPO pour les modèles CHE et CHO. Les CPO pour le modèle CHE est sur l’axe des y, allant de 0,00 à 0,30. Les CPO pour le modèle CHO est sur l’axe des x, allant de 0,00 à 0,25. En général, les valeurs de CPO sont plus élevées pour le modèle CHE que pour le modèle CHO.
Considérons maintenant l’inférence au
sujet de
et
Examinons d’abord
Sous le modèle CHO, la moyenne a posteriori (MP) vaut
0,519, l’écart-type a posteriori (ETP) vaut 0,068 et l’intervalle de
crédibilité à 95 % (Cre) est (0,390;
0,639). Sous le modèle CHE,
MP = 0,515, ETP = 0,065 et Cre
à 95 % est (0,383; 0,639). Ensuite, examinons
Sous le modèle CHO, MP = 0,207,
ETP = 0,011 et Cre à 95 %
est (0,190; 0,224). Sous le modèle CHE,
MP = 0,208, ETP = 0,011 et Cre
à 95 % est (0,190; 0,225). Donc, il est bon de constater que les
inférences au sujet de
et
sont très proches pour les
deux modèles concurrents (modèles CHO et CHE).
Au tableau 3.2, nous présentons
l’inférence a posteriori sur les proportions dans la population finie pour
les notes de mathématique par domaine. Des différences existent entre les
moyennes a posteriori sous les modèles CHO
et CHE. La plupart sont faibles, mais
quelques-unes sont grandes. Pour les domaines NC, SR et CR, nous avons 0,560
(0,543), 0,568 (0,584) et 0,465 (0,445) sous le modèle CHO (CHE), respectivement.
Les écarts-types a posteriori sont également proches, mais il existe
quelques différences modérément grandes (par exemple, pour NR, nous avons 0,113
sous le modèle CHO et 0,077 sous le
modèle CHE). Les intervalles de
crédibilité (Cre) et de densité a posteriori la plus grande (DPPG)
reflètent ces différences.
Tableau 3.2
Comparaison de l’inférence a posteriori d’après les modèles doubles avec corrélation homogène (CHO) et corrélations hétérogènes (CHE) pour les proportions de la population finie pour les élèves américains sous la moyenne en mathématique par domaine
Sommaire du tableau
Le tableau montre les résultats de Comparaison de l’inférence a posteriori d’après les modèles doubles avec corrélation homogène (CHO) et corrélations hétérogènes (CHE) pour les proportions de la population finie pour les élèves américains sous la moyenne en mathématique par domaine. Les données sont présentées selon Domaine (titres de rangée) et Modèle CHO et Modèle CHE (figurant comme en-tête de colonne).
| Domaine |
Modèle CHO |
Modèle CHE |
| MP |
ETP |
Cre à 95 % |
DPPG à 95 % |
MP |
ETP |
Cre à 95 % |
DPPG à 95 % |
| NR |
0,522 |
0,113 |
(0,299; 0,735) |
(0,310; 0,741) |
0,525 |
0,077 |
(0,363; 0,662) |
(0,361; 0,658) |
| NP |
0,365 |
0,075 |
(0,227; 0,524) |
(0,227; 0,520) |
0,359 |
0,072 |
(0,228; 0,511) |
(0,236; 0,516) |
| NC |
0,560 |
0,070 |
(0,420; 0,701) |
(0,408; 0,680) |
0,543 |
0,082 |
(0,370; 0,695) |
(0,396; 0,710) |
| SR |
0,568 |
0,080 |
(0,405; 0,725) |
(0,424; 0,731) |
0,584 |
0,062 |
(0,454; 0,699) |
(0,456; 0,699) |
| SP |
0,537 |
0,058 |
(0,423; 0,648) |
(0,417; 0,639) |
0,537 |
0,063 |
(0,409; 0,655) |
(0,408; 0,653) |
| SC |
0,646 |
0,064 |
(0,552; 0,766) |
(0,522; 0,766) |
0,654 |
0,059 |
(0,521; 0,763) |
(0,544; 0,774) |
| CR |
0,465 |
0,137 |
(0,195; 0,719) |
(0,185; 0,709) |
0,445 |
0,125 |
(0,212; 0,716) |
(0,199; 0,700) |
| CP |
0,437 |
0,085 |
(0,279; 0,603) |
(0,276; 0,596) |
0,439 |
0,091 |
(0,257; 0,620) |
(0,265; 0,620) |
| CC |
0,549 |
0,064 |
(0,415; 0,671) |
(0,423; 0,672) |
0,550 |
0,066 |
(0,414; 0,681) |
(0,422; 0,685) |
| OR |
0,461 |
0,086 |
(0,297; 0,629) |
(0,295; 0,626) |
0,460 |
0,085 |
(0,289; 0,626) |
(0,276; 0,611) |
| OP |
0,516 |
0,066 |
(0,384; 0,643) |
(0,387; 0,644) |
0,516 |
0,058 |
(0,401; 0,626) |
(0,409; 0,633) |
| OC |
0,670 |
0,042 |
(0,581; 0,748) |
(0,586; 0,749) |
0,662 |
0,047 |
(0,569; 0,748) |
(0,568; 0,746) |
Le tableau 3.3 donne les valeurs
sommaires de MP, ETP et DPPG à 95 %
pour les corrélations intragrappe sous le modèle CHE. Nous voyons que les corrélations intragrappe varient d’un
domaine à l’autre. L’estimation la plus élevée est 0,337 pour NC et la plus faible
est 0,073 pour SR. Ces deux domaines présentent quelques grandes différences
entre les moyennes a posteriori sous les modèles CHO et CHE. L’intervalle DPPG à 95 % pour la corrélation commune
dans le modèle CHO, qui est (0,160;
0,260), est contenu par tous les intervalles, sauf ceux pour NR, NC, SR et OC.
Donc, il est raisonnable d’étudier le modèle CHE.
Tableau 3.3
Valeurs sommaires a posteriori pour les corrélations intragrappe des modèles doubles avec corrélations hétérogènes pour les élèves américains sous la moyenne en mathématique par domaine
Sommaire du tableau
Le tableau montre les résultats de Valeurs sommaires a posteriori pour les corrélations intragrappe des modèles doubles avec corrélations hétérogènes pour les élèves américains sous la moyenne en mathématique par domaine. Les données sont présentées selon Domaine (titres de rangée) et MP , ETP , Cre à 95 % et DPPG à 95 % (figurant comme en-tête de colonne).
| Domaine |
MP |
ETP |
Cre à 95 % |
DPPG à 95 % |
| NR |
0,076 |
0,084 |
(0,002; 0,301) |
(0,001; 0,251) |
| NP |
0,184 |
0,087 |
(0,053; 0,380) |
(0,042; 0,358) |
| NC |
0,337 |
0,087 |
(0,190; 0,520) |
(0,184; 0,513) |
| SR |
0,073 |
0,067 |
(0,003; 0,252) |
(0,001; 0,216) |
| SP |
0,237 |
0,075 |
(0,113; 0,393) |
(0,110; 0,387) |
| SC |
0,176 |
0,079 |
(0,055; 0,356) |
(0,048; 0,329) |
| CR |
0,149 |
0,147 |
(0,003; 0,523) |
(0,001; 0,445) |
| CP |
0,233 |
0,103 |
(0,079; 0,486) |
(0,050; 0,434) |
| CC |
0,235 |
0,077 |
(0,105; 0,388) |
(0,099; 0,381) |
| OR |
0,181 |
0,099 |
(0,033; 0,413) |
(0,021; 0,378) |
| OP |
0,181 |
0,075 |
(0,059; 0,362) |
(0,048; 0,327) |
| OC |
0,301 |
0,063 |
(0,191; 0,437) |
(0,188; 0,434) |
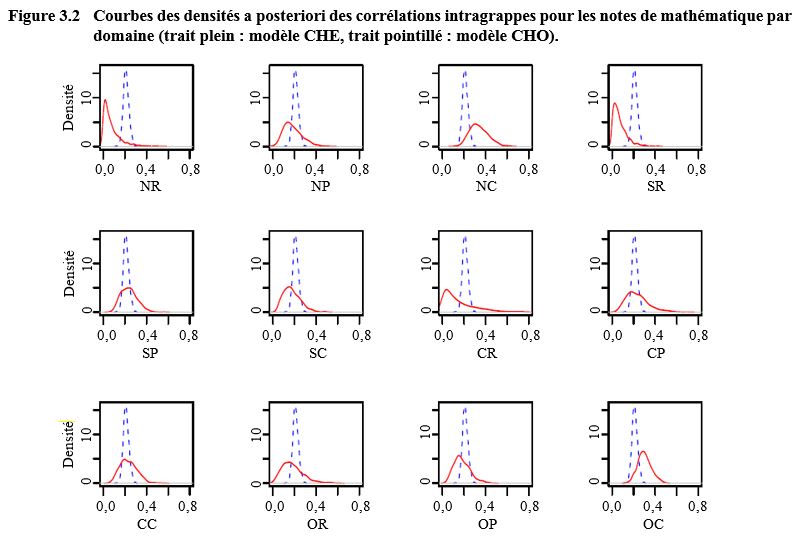
À la figure 3.2, nous comparons
les densités a posteriori des corrélations intragrappe pour le modèle CHE (douze corrélations) et le modèle CHO (une corrélation). Les distributions sous
le modèle CHE sont plus variables, et
elles se situent principalement à la gauche ou à la droite de celles sous le
modèle CHO, le chevauchement étant faible
pour certains domaines (par exemple, NR, NC et SR).
Description de la figure 3.2
Figure composée de douze graphiques présentant les densités a postériori des corrélations intragrappes pour les notes de mathématique, pour chacun des douze domaines (NR, NP, NC, SR, SP, SC, CR, CP, CC, OR, OP et OC) pour les modèles CHE et CHO. Pour chaque graphique, la densité se trouve sur l’axe des y, allant de 0 à 15 et les corrélations se trouvent sur l’axe des x, allant de 0,0 à 0,8. Les distributions sous le modèle CHE sont plus variables, et elles se situent principalement à la gauche ou à la droite de celles sous le modèle CHO. Les domaines NR, NC et SR montrent un faible chevauchement entre les distributions des deux modèles. Les domaines NP, SC, CR, OR, OP et OC montrent un chevauchement un peu plus grand. Finalement, les courbes des domaines SP, CP et CC se chevauchent plus, mais pas complètement.
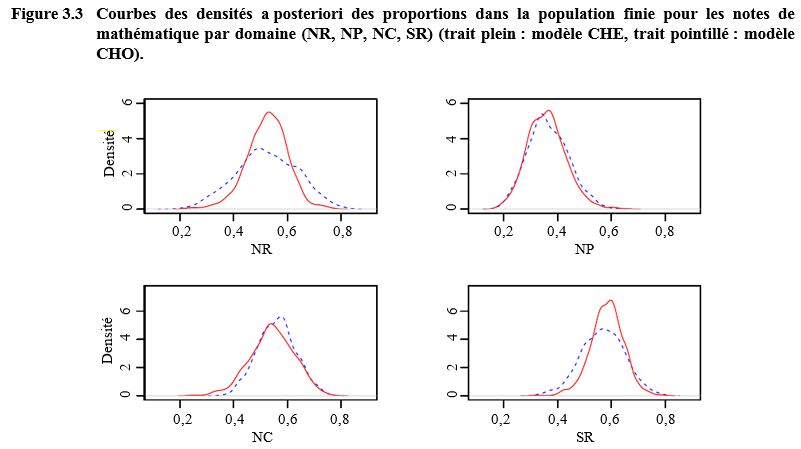
Aux figures 3.3, 3.4 et 3.5, nous
comparons les courbes des densités a posteriori des proportions de la
population finie pour les notes de mathématique par domaine pour les deux
modèles. Des différences appréciables s’observent entre les modèles CHO et CHE
(par exemple, domaines NR, NC, SR, CR et OC).
Description de la figure 3.3
Figure composée de quatre graphiques présentant les densités a postériori des proportions dans la population finie pour les notes de mathématique pour les domaines (NR, NP, NC et SR) pour les modèles CHE et CHO. Pour chaque graphique, la densité se trouve sur l’axe des y, allant de 0 à 6 et les corrélations se trouvent sur l’axe des x, allant de 0,0 à 0,8. Des différences appréciables s’observent entre les modèles CHO et CHE pour les domaines NR, NC et SR. Les distributions sont plus proches pour le domaine NP.
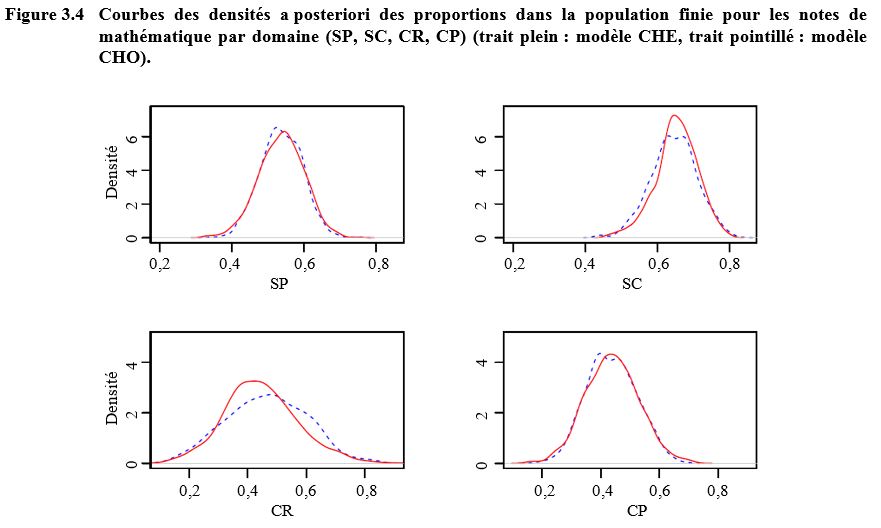
Description de la figure 3.4
Figure composée de quatre graphiques présentant les densités a postériori des proportions dans la population finie pour les notes de mathématique pour les domaines (SP, SC, CR et CP) pour les modèles CHE et CHO. Pour chaque graphique, la densité se trouve sur l’axe des y, allant de 0 à 6 et les corrélations se trouvent sur l’axe des x, allant de 0,0 à 0,8. Des différences appréciables s’observent entre les modèles CHO et CHE pour le domaine CR. Les distributions sont plus proches pour les domaines SP, SC et CP.
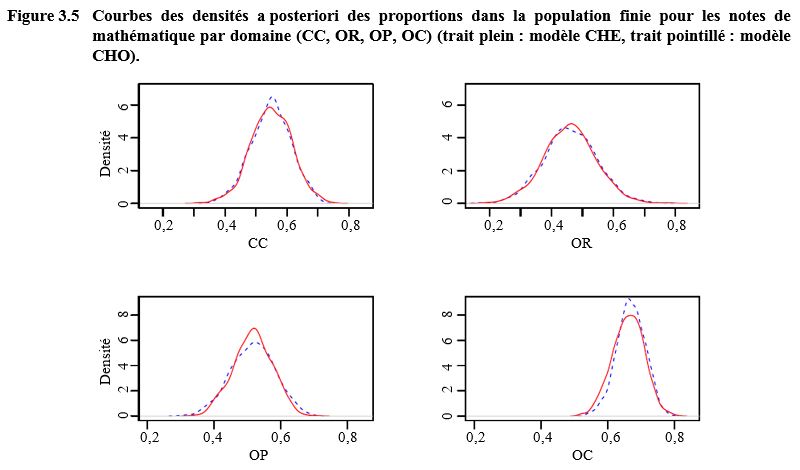
Description de la figure 3.5
Figure composée de quatre graphiques présentant les densités a postériori des proportions dans la population finie pour les notes de mathématique pour les domaines (CC, OR, OP et OC) pour les modèles CHE et CHO. Pour chaque graphique, la densité se trouve sur l’axe des y, allant de 0 à 6 pour CC et OR et de 0 à 8 pour OP et OC et les corrélations se trouvent sur l’axe des x, allant de 0,0 à 0,8. Des différences appréciables s’observent entre les modèles CHO et CHE pour le domaine OC. Les distributions sont plus proches pour les domaines CC, OR et OP.
3.2 Étude en simulation
Une étude en simulation nous permet de
poursuivre l’évaluation de la performance du modèle CHE en vue de la comparer à celle du modèle CHO. Ici, nous utilisons deux facteurs, présentant chacun trois
niveaux, pour obtenir neuf points de référence.
Nous avons fixé à 100 le nombre de
grappes (écoles) dans chaque domaine et à 15 le nombre d’individus (élèves)
dans chaque grappe. Autrement dit, nous prenons
où
Désignons par
un vecteur de moyennes a posteriori
et par
, le vecteur des écarts-types a posteriori correspondant aux
ou aux
Plus précisément, pour les
nous utilisons
et
et pour les
nous utilisons
et
Quand nous simulons les
données à partir du modèle CHE, les
niveaux des
sont
et les niveaux des
sont
Pour les douze domaines,
prend les valeurs 0,09; 0,19;
0,32; 0,08; 0,22; 0,18; 0,15; 0,22; 0,23; 0,17; 0,18; 0,30;
prend les valeurs 0,08; 0,09;
0,08; 0,06; 0,07; 0,08; 0,13; 0,09; 0,07; 0,09; 0,07; 0,06;
prend les valeurs 0,53; 0,37;
0,54; 0,58; 0,54; 0,65; 0,46; 0,44; 0,55; 0,46; 0,52; 0,66; et
prend les valeurs 0,08; 0,08;
0,08; 0,06; 0,06; 0,06; 0,12; 0,09; 0,07; 0,08; 0,06; 0,05.
Nous tirons aussi un échantillon
aléatoire simple de cinq grappes parmi les 100 grappes de la population,
ainsi qu’un échantillon aléatoire simple de dix individus dans chaque grappe
échantillonnée (c’est-à-dire
et
Ces nombres sont nettement
plus faibles que ceux pour les données utilisées à la section 3.1, ce qui
rend l’inférence un peu plus difficile (Nandram
2015). Notons que l’ensemble de données contient environ 7 % de grappes
échantillonnées où tous les élèves étaient soit en dessous ou au-dessus de la
moyenne. Nous nommons cette quantité le pourcentage de données éparses. La
configuration de la présente étude en simulation donne lieu à des données
encore plus éparses. Pour neuf points de référence, tous les pourcentages
moyens de données éparses sont supérieurs à 7 % et la plupart sont de
l’ordre de 10 %. La figure 3.6 montre les histogrammes des
pourcentages de données éparses pour chaque point de référence.
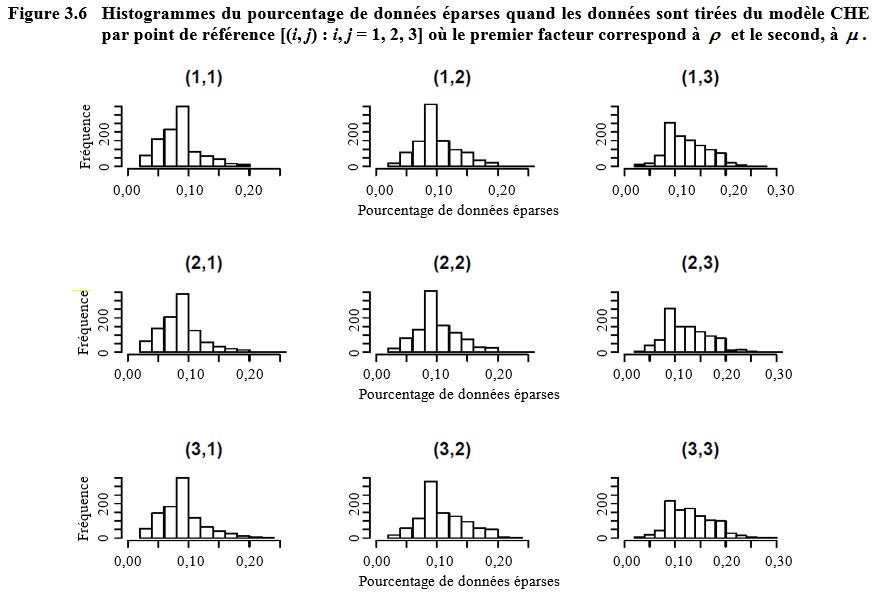
Description de la figure 3.6
Figure composée de neuf graphiques présentant les histogrammes des pourcentages de données éparses quand les données sont tirées du modèle CHE, par point de référence où le premier facteur correspond à et le second, à Pour chaque graphique, la fréquence se trouve sur l’axe des y, allant de 0 à 200 et le pourcentage de données éparses se trouve sur l’axe des x, allant de 0,00 à 0,30 quand et de 0,00 à 0,20 sinon. Pour les trois graphiques où le pourcentage de données éparses culmine à environ 10 %, avec une plus grande fréquence sous qu’au-dessus de 10 %. Pour les trois graphiques où le pourcentage de données éparses culmine à environ 10 %, avec une plus grande fréquence au-dessus que sous 10 %. Pour les trois graphiques où le pourcentage de données éparses culmine à environ 10 %, avec une fréquence très faible pour les pourcentages plus petits que 10 %.
Nous étudions deux scénarios. Dans le premier, nous générons des
données à partir du modèle CHE et
ajustons les deux modèles, et dans le second, nous générons des données à
partir du modèle CHO et ajustons les deux
modèles. Dans le cas des données simulées à partir du modèle CHE, nous avons neuf points de référence
et le premier facteur
correspond à
Quand nous simulons les
données à partir du modèle CHO, nous
avons trois points de référence
pour les trois niveaux pour
les
la valeur de
est maintenue fixe à sa
moyenne a posteriori.
Dans le premier scénario, à chaque point de référence, nous simulons
des données binaires à partir du modèle CHE,
Donc, nous avons les
vraies valeurs de
pour
Nous tirons 1 000 échantillons à
chacun des neuf points de référence. Pour chaque échantillon, nous exécutons
l’échantillonneur de Gibbs « à grille »
par blocs de la même façon que pour les données.
Comme Nandram (2015), nous
calculons
et
pour étudier les propriétés
fréquentistes de notre procédure
Nous obtenons aussi les intervalles
de crédibilité et DPPG à 95 % pour
chacune des 1 000 exécutions de la simulation, et nous étudions la
largeur
et l’incidence de crédibilité
Si l’intervalle de
crédibilité (ou DPPG) à 95 % de la
exécution contient la valeur
réelle
est égale à un, sinon elle
est nulle. Donc, le contenu probabiliste estimé de l’intervalle de crédibilité
à 95 % pour le
domaine est
Le tableau 3.4 donne la comparaison des modèles CHO et CHE.
Les couvertures sont clairement plus élevées sous le modèle CHE que sous le modèle CHO. Notons que les couvertures des intervalles DPPG pour le modèle CHE sont nettement plus proches de la valeur nominale de 95 %
et sont conservatrices. Cependant, les intervalles de crédibilité et DPPG à
95 % sont plus larges que sous le modèle CHO.
Ces effets deviennent beaucoup plus importants à mesure que
augmente. Les mesures BA, BAR
et REQMP sont toutes plus petites sous le modèle CHE que sous le modèle CHO.
Donc, en s’appuyant sur ces mesures, la préférence est donnée au modèle CHE plutôt qu’au modèle CHO.
Tableau 3.4
Simulation sous le modèle CHE : Comparaison des modèles CHE et CHO en utilisant la couverture moyenne et la largeur des intervalles de crédibilité à 95 % et le biais absolu, le biais absolu relatif et la racine carrée de l’erreur quadratique moyenne a posteriori pour les proportions de la population finie par point de référence
Sommaire du tableau
Le tableau montre les résultats de Simulation sous le modèle CHE : Comparaison des modèles CHE et CHO en utilisant la couverture moyenne et la largeur des intervalles de crédibilité à 95 % et le biais absolu. Les données sont présentées selon Point de référence (titres de rangée) et Modèle , C-Cre , L-Cre , C-DPPG , L-DPPG, BA , BAR et REQMP (figurant comme en-tête de colonne).
| Point de référence |
Modèle |
C-Cre |
L-Cre |
C-DPPG |
L-DPPG |
BA |
BAR |
REQMP |
| (1,1) |
CHE |
0,989 |
0,620 |
0,961 |
0,603 |
0,112 |
0,227 |
0,206 |
| CHO |
0,930 |
0,555 |
0,893 |
0,541 |
0,130 |
0,266 |
0,207 |
| (1,2) |
CHE |
0,984 |
0,622 |
0,960 |
0,603 |
0,112 |
0,227 |
0,206 |
| CHO |
0,926 |
0,558 |
0,889 |
0,545 |
0,132 |
0,249 |
0,209 |
| (1,3) |
CHE |
0,980 |
0,623 |
0,955 |
0,608 |
0,120 |
0,211 |
0,210 |
| CHO |
0,923 |
0,558 |
0,892 |
0,546 |
0,134 |
0,236 |
0,212 |
| (2,1) |
CHE |
0,982 |
0,621 |
0,953 |
0,603 |
0,119 |
0,242 |
0,212 |
| CHO |
0,922 |
0,564 |
0,879 |
0,549 |
0,137 |
0,281 |
0,215 |
| (2,2) |
CHE |
0,980 |
0,625 |
0,952 |
0,609 |
0,122 |
0,228 |
0,214 |
| CHO |
0,918 |
0,566 |
0,879 |
0,552 |
0,139 |
0,264 |
0,217 |
| (2,3) |
CHE |
0,981 |
0,628 |
0,956 |
0,611 |
0,121 |
0,211 |
0,214 |
| CHO |
0,930 |
0,570 |
0,895 |
0,556 |
0,135 |
0,239 |
0,214 |
| (3,1) |
CHE |
0,982 |
0,627 |
0,949 |
0,608 |
0,121 |
0,245 |
0,215 |
| CHO |
0,934 |
0,583 |
0,892 |
0,566 |
0,136 |
0,278 |
0,218 |
| (3,2) |
CHE |
0,980 |
0,628 |
0,947 |
0,610 |
0,123 |
0,242 |
0,217 |
| CHO |
0,928 |
0,583 |
0,885 |
0,566 |
0,138 |
0,274 |
0,220 |
| (3,3) |
CHE |
0,976 |
0,632 |
0,951 |
0,614 |
0,124 |
0,218 |
0,218 |
| CHO |
0,928 |
0,581 |
0,889 |
0,565 |
0,139 |
0,246 |
0,220 |
Dans le tableau 3.5, nous
comparons les données sommaires pour les critères DIC, BPP et LPML. Toutes les
valeurs de DIC sous le modèle CHE sont
plus faibles que les valeurs correspondantes sous le modèle CHO, et toutes les valeurs de LPML sous le
modèle CHE sont plus grandes que celles
sous le modèle CHO. Sous le modèle CHO, toutes les valeurs de BPP varient dans
l’intervalle (0,06; 0,09), mais sous le modèle
CHE, elles varient dans l’intervalle (0,2; 0,4).
De nouveau, ces mesures montrent que le modèle CHE
donne de meilleurs résultats que le modèle CHO.
De façon similaire, pour le deuxième
scénario, nous générons des données binaires à partir de
Dans
le tableau 3.6, nous comparons les modèles CHO
et CHE. Ici, les critères BA, BAR et
REQMP ne sont que légèrement plus faibles sous le modèle CHO. Les couvertures des intervalles de
crédibilité et DPPG sous le modèle CHE s’approchent davantage de la valeur
nominale de 95 %, tandis que celles sous le modèle CHO sont plus petites. Le tableau 3.7 donne les données
sommaires pour les critères DIC, BPP et LPML. Toutes les valeurs de DIC sous le
modèle CHE sont plus petites que sous le
modèle CHO, tandis que les valeurs de BPP
et de LPML sont similaires pour les deux modèles, celles obtenues sous le
modèle CHO étant légèrement meilleures.
Tableau 3.5
Simulation sous le modèle CHE : Comparaison des modèles CHE et CHO en utilisant le critère d’information de déviance (DIC), la valeur p prédictive bayésienne (BPP) et le logarithme de la pseudo-vraisemblance marginale (LPML) par point de référence
Sommaire du tableau
Le tableau montre les résultats de Simulation sous le modèle CHE : Comparaison des modèles CHE et CHO en utilisant le critère d’information de déviance (DIC). Les données sont présentées selon Point de référence (titres de rangée) et Modèle CHO et Modèle CHE (figurant comme en-tête de colonne).
| Point de référence |
Modèle CHO |
Modèle CHE |
| DIC |
BPP |
LPML |
DIC |
BPP |
LPML |
| (1,1) |
419,275 |
0,090 |
-285,452 |
402,044 |
0,429 |
-267,990 |
| (1,2) |
418,351 |
0,091 |
-286,250 |
400,647 |
0,439 |
-266,377 |
| (1,3) |
416,784 |
0,088 |
-286,290 |
400,414 |
0,446 |
-267,203 |
| (2,1) |
436,980 |
0,067 |
-307,028 |
416,264 |
0,300 |
-292,756 |
| (2,2) |
437,306 |
0,062 |
-308,816 |
414,955 |
0,318 |
-292,404 |
| (2,3) |
430,531 |
0,080 |
-302,258 |
410,436 |
0,351 |
-285,206 |
| (3,1) |
441,204 |
0,090 |
-316,126 |
424,010 |
0,227 |
-308,825 |
| (3,2) |
442,165 |
0,083 |
-318,223 |
424,363 |
0,235 |
-309,815 |
| (3,3) |
438,305 |
0,071 |
-315,159 |
418,827 |
0,260 |
-306,619 |
Tableau 3.6
Simulation sous le modèle CHO : Comparaison des modèles CHE et CHO en utilisant la couverture moyenne et la largeur des intervalles de crédibilité à 95 % et le biais absolu, le biais absolu relatif et la racine carrée de l’erreur quadratique moyenne a posteriori pour les proportions de la population finie par point de référence
Sommaire du tableau
Le tableau montre les résultats de Simulation sous le modèle CHO : Comparaison des modèles CHE et CHO en utilisant la couverture moyenne et la largeur des intervalles de crédibilité à 95 % et le biais absolu. Les données sont présentées selon Point de référence (titres de rangée) et Modèle , C-Cre , L-Cre , C-DPPG , L-DPPG, BA , BAR et REQMP (figurant comme en-tête de colonne).
| Point de référence |
Modèle |
C-Cre |
L-Cre |
C-DPPG |
L-DPPG |
BA |
BAR |
REQMP |
| 1 |
CHE |
0,985 |
0,627 |
0,969 |
0,608 |
0,117 |
0,242 |
0,212 |
| CHO |
0,944 |
0,575 |
0,919 |
0,559 |
0,107 |
0,240 |
0,210 |
| 2 |
CHE |
0,988 |
0,634 |
0,952 |
0,616 |
0,122 |
0,234 |
0,216 |
| CHO |
0,938 |
0,585 |
0,917 |
0,568 |
0,115 |
0,214 |
0,211 |
| 3 |
CHE |
0,977 |
0,628 |
0,940 |
0,611 |
0,126 |
0,222 |
0,218 |
| CHO |
0,933 |
0,572 |
0,908 |
0,556 |
0,113 |
0,202 |
0,208 |
Tableau 3.7
Simulation sous le modèle CHO : Comparaison des modèles CHE et CHO en utilisant le critère d’information de déviance (DIC), la valeur p prédictive bayésienne (BPP) et le logarithme de la pseudo-vraisemblance marginale (LPML) par point de référence
Sommaire du tableau
Le tableau montre les résultats de Simulation sous le modèle CHO : Comparaison des modèles CHE et CHO en utilisant le critère d’information de déviance (DIC). Les données sont présentées selon Point de référence (titres de rangée) et Modèle CHO et Modèle CHE (figurant comme en-tête de colonne).
| Point de référence |
Modèle CHO |
Modèle CHE |
| DIC |
BPP |
LPML |
DIC |
BPP |
LPML |
| 1 |
428,647 |
0,308 |
-300,526 |
416,626 |
0,302 |
-303,001 |
| 2 |
430,113 |
0,371 |
-295,191 |
417,557 |
0,317 |
-296,531 |
| 3 |
429,598 |
0,379 |
-295,613 |
414,877 |
0,335 |
-297,250 |
Donc, quand les données sont
effectivement issues du modèle CHE, nous
constatons certaines différences importantes entre les deux modèles, la
préférence étant donnée au modèle CHE.
Par contre, quand les données proviennent du modèle CHO, les différences constatées entre les deux modèles sont
mineures. Bien entendu, le modèle CHE
(corrélations inégales) contient plus de paramètres que le modèle CHO (une corrélation).





