Carte 2
Concentration de la population de langue officielle minoritaire et des travailleurs du secteur agroalimentaire, population âgée de 15 ans et plus, subdivisions de recensement (SDR) et régions agricoles, Ontario, 2011
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
Description de la Carte 2
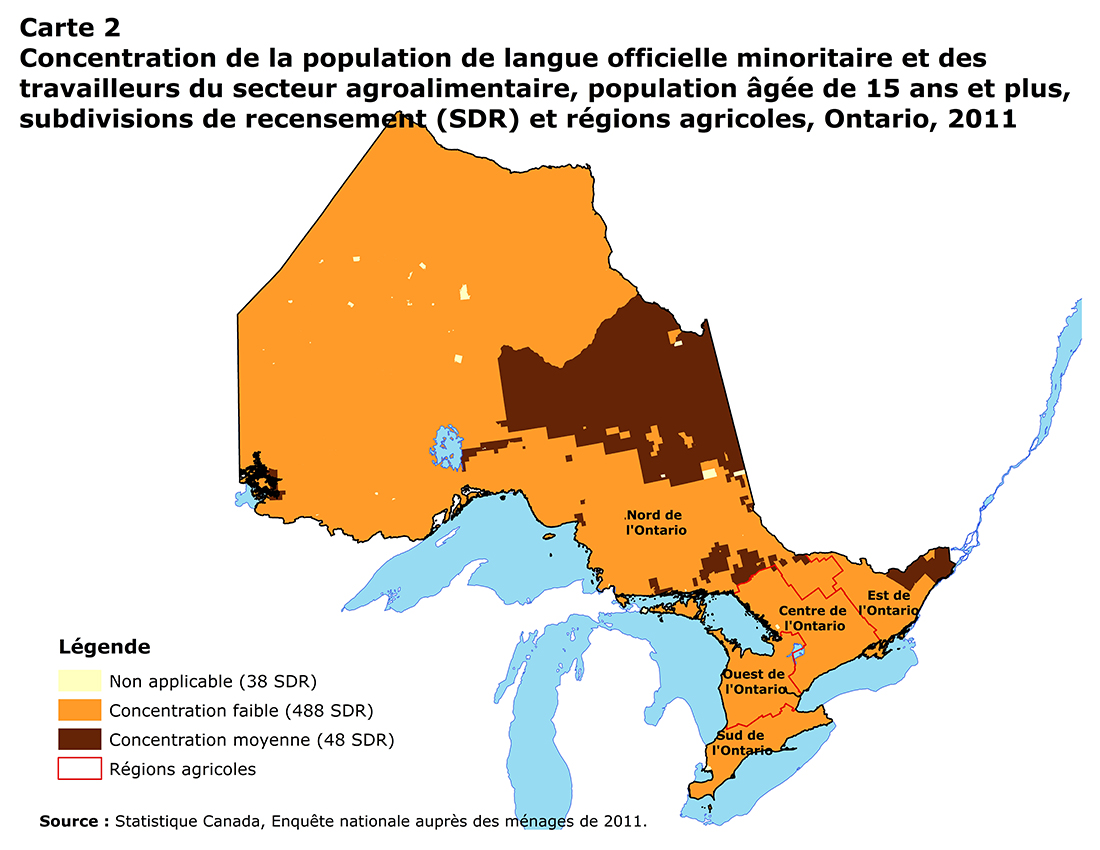
Concentration de la population de langue officielle minoritaire et des travailleurs du secteur agroalimentaire, population âgée de 15 ans et plus, subdivisions de recensement (SDR) et régions agricoles, Ontario, 2011
Cette carte montre la concentration de la population de langue officielle minoritaire et des travailleurs du secteur agroalimentaire par subdivisions de recensement (SDR) et régions agricoles en Ontario.
Pour cette carte, on utilise quatre couleurs distinctes. Le jaune signifie « Non applicable » et regroupe 38 SDRs. L’orange indique une « concentration faible » et regroupe 488 SDRs. Enfin, le brun est utilisé pour indiquer une « concentration moyenne » et regroupe 48 SDRs. ». Chaque région agricole est délimitée par une ligne rouge. La source de cette carte est : Statistique Canada, Enquête nationale auprès des ménages, 2011. Chaque région est colorée selon le tableau ci-dessous :
| SDR | Minorités de langue officielle et travailleurs du secteur agroalimentaire | |
|---|---|---|
| Code | Concentration | |
| 3538004 | 0 | Non applicable |
| 3544071 | 0 | Non applicable |
| 3548072 | 0 | Non applicable |
| 3551034 | 0 | Non applicable |
| 3554091 | 0 | Non applicable |
| 3557075 | 0 | Non applicable |
| 3557077 | 0 | Non applicable |
| 3558077 | 0 | Non applicable |
| 3558095 | 0 | Non applicable |
| 3558100 | 0 | Non applicable |
| 3559048 | 0 | Non applicable |
| 3559052 | 0 | Non applicable |
| 3559062 | 0 | Non applicable |
| 3560051 | 0 | Non applicable |
| 3560053 | 0 | Non applicable |
| 3560059 | 0 | Non applicable |
| 3560067 | 0 | Non applicable |
| 3560093 | 0 | Non applicable |
| 3560095 | 0 | Non applicable |
| 3560096 | 0 | Non applicable |
| 3560098 | 0 | Non applicable |
| 3560100 | 0 | Non applicable |
| 3560102 | 0 | Non applicable |
| 3560071 | 0 | Non applicable |
| 3560076 | 0 | Non applicable |
| 3560077 | 0 | Non applicable |
| 3560079 | 0 | Non applicable |
| 3560081 | 0 | Non applicable |
| 3560085 | 0 | Non applicable |
| 3560086 | 0 | Non applicable |
| 3559065 | 0 | Non applicable |
| 3560007 | 0 | Non applicable |
| 3557094 | 0 | Non applicable |
| 3556091 | 0 | Non applicable |
| 3556094 | 0 | Non applicable |
| 3556096 | 0 | Non applicable |
| 3556100 | 0 | Non applicable |
| 3501007 | 0 | Non applicable |
| 3501005 | 2 | Moyenne |
| 3501011 | 2 | Moyenne |
| 3501012 | 2 | Moyenne |
| 3501020 | 1 | Faible |
| 3501030 | 1 | Faible |
| 3501042 | 2 | Moyenne |
| 3501050 | 2 | Moyenne |
| 3502001 | 2 | Moyenne |
| 3502008 | 2 | Moyenne |
| 3502010 | 2 | Moyenne |
| 3502023 | 1 | Faible |
| 3502025 | 2 | Moyenne |
| 3502036 | 2 | Moyenne |
| 3502044 | 2 | Moyenne |
| 3502048 | 2 | Moyenne |
| 3506008 | 2 | Moyenne |
| 3507004 | 1 | Faible |
| 3507006 | 1 | Faible |
| 3507008 | 1 | Faible |
| 3507014 | 1 | Faible |
| 3507015 | 1 | Faible |
| 3507017 | 1 | Faible |
| 3507021 | 1 | Faible |
| 3507024 | 1 | Faible |
| 3507033 | 1 | Faible |
| 3507040 | 1 | Faible |
| 3507042 | 1 | Faible |
| 3507052 | 1 | Faible |
| 3507065 | 1 | Faible |
| 3509001 | 1 | Faible |
| 3509004 | 1 | Faible |
| 3509010 | 1 | Faible |
| 3509015 | 1 | Faible |
| 3509021 | 1 | Faible |
| 3509024 | 1 | Faible |
| 3509028 | 1 | Faible |
| 3509030 | 1 | Faible |
| 3509039 | 1 | Faible |
| 3510005 | 1 | Faible |
| 3510010 | 1 | Faible |
| 3510020 | 1 | Faible |
| 3510035 | 1 | Faible |
| 3510045 | 1 | Faible |
| 3511005 | 1 | Faible |
| 3511015 | 1 | Faible |
| 3511030 | 1 | Faible |
| 3511035 | 1 | Faible |
| 3512001 | 1 | Faible |
| 3512002 | 1 | Faible |
| 3512004 | 1 | Faible |
| 3512005 | 1 | Faible |
| 3512015 | 1 | Faible |
| 3512020 | 1 | Faible |
| 3512026 | 1 | Faible |
| 3512030 | 1 | Faible |
| 3512036 | 1 | Faible |
| 3512046 | 1 | Faible |
| 3512048 | 1 | Faible |
| 3512051 | 1 | Faible |
| 3512054 | 1 | Faible |
| 3512058 | 1 | Faible |
| 3512061 | 1 | Faible |
| 3512065 | 1 | Faible |
| 3512076 | 1 | Faible |
| 3513020 | 1 | Faible |
| 3514004 | 1 | Faible |
| 3514014 | 1 | Faible |
| 3514019 | 1 | Faible |
| 3514020 | 1 | Faible |
| 3514021 | 1 | Faible |
| 3514024 | 1 | Faible |
| 3514027 | 1 | Faible |
| 3514045 | 1 | Faible |
| 3515003 | 1 | Faible |
| 3515005 | 1 | Faible |
| 3515008 | 1 | Faible |
| 3515013 | 1 | Faible |
| 3515014 | 1 | Faible |
| 3515015 | 1 | Faible |
| 3515019 | 1 | Faible |
| 3515023 | 1 | Faible |
| 3515030 | 1 | Faible |
| 3515037 | 1 | Faible |
| 3515044 | 1 | Faible |
| 3516010 | 1 | Faible |
| 3518001 | 1 | Faible |
| 3518005 | 1 | Faible |
| 3518009 | 1 | Faible |
| 3518013 | 1 | Faible |
| 3518017 | 1 | Faible |
| 3518020 | 1 | Faible |
| 3518022 | 1 | Faible |
| 3518029 | 1 | Faible |
| 3518039 | 1 | Faible |
| 3519028 | 1 | Faible |
| 3519036 | 1 | Faible |
| 3519038 | 1 | Faible |
| 3519044 | 1 | Faible |
| 3519046 | 1 | Faible |
| 3519048 | 1 | Faible |
| 3519049 | 1 | Faible |
| 3519054 | 1 | Faible |
| 3519070 | 1 | Faible |
| 3519076 | 1 | Faible |
| 3520005 | 1 | Faible |
| 3521005 | 1 | Faible |
| 3521010 | 1 | Faible |
| 3521024 | 1 | Faible |
| 3522001 | 1 | Faible |
| 3522008 | 1 | Faible |
| 3522010 | 1 | Faible |
| 3522012 | 1 | Faible |
| 3522014 | 1 | Faible |
| 3522016 | 1 | Faible |
| 3522019 | 1 | Faible |
| 3522021 | 1 | Faible |
| 3523001 | 1 | Faible |
| 3523008 | 1 | Faible |
| 3523009 | 1 | Faible |
| 3523017 | 1 | Faible |
| 3523025 | 1 | Faible |
| 3523033 | 1 | Faible |
| 3523043 | 1 | Faible |
| 3523050 | 1 | Faible |
| 3524001 | 1 | Faible |
| 3524002 | 1 | Faible |
| 3524009 | 1 | Faible |
| 3524015 | 1 | Faible |
| 3525005 | 1 | Faible |
| 3526003 | 1 | Faible |
| 3526011 | 1 | Faible |
| 3526014 | 1 | Faible |
| 3526021 | 1 | Faible |
| 3526028 | 1 | Faible |
| 3526032 | 1 | Faible |
| 3526037 | 1 | Faible |
| 3526043 | 1 | Faible |
| 3526047 | 1 | Faible |
| 3526053 | 1 | Faible |
| 3526057 | 1 | Faible |
| 3526065 | 1 | Faible |
| 3528018 | 1 | Faible |
| 3528035 | 1 | Faible |
| 3528037 | 1 | Faible |
| 3528052 | 1 | Faible |
| 3529005 | 1 | Faible |
| 3529006 | 1 | Faible |
| 3529020 | 1 | Faible |
| 3529021 | 1 | Faible |
| 3530004 | 1 | Faible |
| 3530010 | 1 | Faible |
| 3530013 | 1 | Faible |
| 3530016 | 1 | Faible |
| 3530020 | 1 | Faible |
| 3530027 | 1 | Faible |
| 3530035 | 1 | Faible |
| 3531011 | 1 | Faible |
| 3531013 | 1 | Faible |
| 3531016 | 1 | Faible |
| 3531025 | 1 | Faible |
| 3531030 | 1 | Faible |
| 3531040 | 1 | Faible |
| 3532002 | 1 | Faible |
| 3532004 | 1 | Faible |
| 3532012 | 1 | Faible |
| 3532018 | 1 | Faible |
| 3532027 | 1 | Faible |
| 3532038 | 1 | Faible |
| 3532042 | 1 | Faible |
| 3532045 | 1 | Faible |
| 3534005 | 1 | Faible |
| 3534010 | 1 | Faible |
| 3534011 | 1 | Faible |
| 3534020 | 1 | Faible |
| 3534021 | 1 | Faible |
| 3534024 | 1 | Faible |
| 3534030 | 1 | Faible |
| 3534042 | 1 | Faible |
| 3536020 | 1 | Faible |
| 3536029 | 1 | Faible |
| 3537001 | 1 | Faible |
| 3537003 | 1 | Faible |
| 3537013 | 1 | Faible |
| 3537016 | 1 | Faible |
| 3537028 | 1 | Faible |
| 3537034 | 1 | Faible |
| 3537039 | 1 | Faible |
| 3537048 | 1 | Faible |
| 3537064 | 1 | Faible |
| 3538003 | 1 | Faible |
| 3538007 | 1 | Faible |
| 3538015 | 1 | Faible |
| 3538016 | 1 | Faible |
| 3538018 | 1 | Faible |
| 3538019 | 1 | Faible |
| 3538025 | 1 | Faible |
| 3538030 | 1 | Faible |
| 3538031 | 1 | Faible |
| 3538035 | 1 | Faible |
| 3538040 | 1 | Faible |
| 3538043 | 1 | Faible |
| 3538056 | 1 | Faible |
| 3539002 | 1 | Faible |
| 3539005 | 1 | Faible |
| 3539015 | 1 | Faible |
| 3539017 | 1 | Faible |
| 3539018 | 1 | Faible |
| 3539021 | 1 | Faible |
| 3539027 | 1 | Faible |
| 3539033 | 1 | Faible |
| 3539036 | 1 | Faible |
| 3539041 | 1 | Faible |
| 3539047 | 1 | Faible |
| 3539060 | 1 | Faible |
| 3540005 | 1 | Faible |
| 3540010 | 1 | Faible |
| 3540025 | 1 | Faible |
| 3540028 | 1 | Faible |
| 3540040 | 1 | Faible |
| 3540046 | 1 | Faible |
| 3540050 | 1 | Faible |
| 3540055 | 1 | Faible |
| 3540063 | 1 | Faible |
| 3541004 | 1 | Faible |
| 3541015 | 1 | Faible |
| 3541024 | 1 | Faible |
| 3541032 | 1 | Faible |
| 3541043 | 1 | Faible |
| 3541045 | 1 | Faible |
| 3541055 | 1 | Faible |
| 3541057 | 1 | Faible |
| 3541060 | 1 | Faible |
| 3541069 | 1 | Faible |
| 3542004 | 1 | Faible |
| 3542005 | 1 | Faible |
| 3542015 | 1 | Faible |
| 3542029 | 1 | Faible |
| 3542037 | 1 | Faible |
| 3542045 | 1 | Faible |
| 3542047 | 1 | Faible |
| 3542053 | 1 | Faible |
| 3542059 | 1 | Faible |
| 3543003 | 1 | Faible |
| 3543005 | 1 | Faible |
| 3543007 | 1 | Faible |
| 3543009 | 1 | Faible |
| 3543014 | 1 | Faible |
| 3543015 | 1 | Faible |
| 3543017 | 1 | Faible |
| 3543019 | 1 | Faible |
| 3543021 | 1 | Faible |
| 3543023 | 1 | Faible |
| 3543031 | 1 | Faible |
| 3543042 | 1 | Faible |
| 3543050 | 1 | Faible |
| 3543052 | 1 | Faible |
| 3543064 | 1 | Faible |
| 3543068 | 1 | Faible |
| 3543069 | 1 | Faible |
| 3543070 | 1 | Faible |
| 3543071 | 1 | Faible |
| 3543072 | 1 | Faible |
| 3543074 | 1 | Faible |
| 3544002 | 1 | Faible |
| 3544018 | 1 | Faible |
| 3544027 | 1 | Faible |
| 3544042 | 1 | Faible |
| 3544053 | 1 | Faible |
| 3544065 | 1 | Faible |
| 3544073 | 1 | Faible |
| 3546005 | 1 | Faible |
| 3546015 | 1 | Faible |
| 3546018 | 1 | Faible |
| 3546024 | 1 | Faible |
| 3547002 | 1 | Faible |
| 3547003 | 1 | Faible |
| 3547008 | 1 | Faible |
| 3547020 | 1 | Faible |
| 3547030 | 1 | Faible |
| 3547033 | 1 | Faible |
| 3547035 | 1 | Faible |
| 3547037 | 1 | Faible |
| 3547043 | 1 | Faible |
| 3547046 | 1 | Faible |
| 3547048 | 1 | Faible |
| 3547056 | 1 | Faible |
| 3547064 | 1 | Faible |
| 3547070 | 1 | Faible |
| 3547075 | 1 | Faible |
| 3547076 | 1 | Faible |
| 3547090 | 1 | Faible |
| 3547096 | 1 | Faible |
| 3547098 | 1 | Faible |
| 3548001 | 1 | Faible |
| 3548013 | 2 | Moyenne |
| 3548019 | 1 | Faible |
| 3548021 | 2 | Moyenne |
| 3548022 | 1 | Faible |
| 3548027 | 2 | Moyenne |
| 3548031 | 1 | Faible |
| 3548034 | 1 | Faible |
| 3548044 | 2 | Moyenne |
| 3548055 | 2 | Moyenne |
| 3548069 | 1 | Faible |
| 3548073 | 1 | Faible |
| 3548091 | 1 | Faible |
| 3548094 | 1 | Faible |
| 3549003 | 1 | Faible |
| 3549005 | 1 | Faible |
| 3549012 | 1 | Faible |
| 3549014 | 1 | Faible |
| 3549018 | 1 | Faible |
| 3549019 | 1 | Faible |
| 3549022 | 1 | Faible |
| 3549024 | 1 | Faible |
| 3549028 | 1 | Faible |
| 3549031 | 1 | Faible |
| 3549032 | 1 | Faible |
| 3549036 | 1 | Faible |
| 3549039 | 1 | Faible |
| 3549043 | 1 | Faible |
| 3549046 | 1 | Faible |
| 3549048 | 1 | Faible |
| 3549051 | 1 | Faible |
| 3549054 | 1 | Faible |
| 3549056 | 1 | Faible |
| 3549060 | 1 | Faible |
| 3549066 | 2 | Moyenne |
| 3549071 | 1 | Faible |
| 3549072 | 1 | Faible |
| 3549073 | 1 | Faible |
| 3549075 | 1 | Faible |
| 3549076 | 1 | Faible |
| 3549077 | 1 | Faible |
| 3549078 | 1 | Faible |
| 3549095 | 1 | Faible |
| 3549096 | 1 | Faible |
| 3551001 | 1 | Faible |
| 3551006 | 1 | Faible |
| 3551011 | 1 | Faible |
| 3551017 | 1 | Faible |
| 3551021 | 1 | Faible |
| 3551026 | 1 | Faible |
| 3551027 | 1 | Faible |
| 3551028 | 1 | Faible |
| 3551040 | 1 | Faible |
| 3551041 | 1 | Faible |
| 3551042 | 1 | Faible |
| 3551043 | 1 | Faible |
| 3551044 | 1 | Faible |
| 3551045 | 1 | Faible |
| 3551094 | 1 | Faible |
| 3551100 | 1 | Faible |
| 3552001 | 2 | Moyenne |
| 3552004 | 2 | Moyenne |
| 3552013 | 1 | Faible |
| 3552023 | 1 | Faible |
| 3552026 | 2 | Moyenne |
| 3552028 | 2 | Moyenne |
| 3552031 | 1 | Faible |
| 3552036 | 1 | Faible |
| 3552051 | 1 | Faible |
| 3552052 | 1 | Faible |
| 3552053 | 1 | Faible |
| 3552054 | 1 | Faible |
| 3552058 | 1 | Faible |
| 3552092 | 2 | Moyenne |
| 3552093 | 1 | Faible |
| 3553005 | 2 | Moyenne |
| 3553040 | 1 | Faible |
| 3554001 | 1 | Faible |
| 3554006 | 1 | Faible |
| 3554008 | 2 | Moyenne |
| 3554014 | 2 | Moyenne |
| 3554020 | 2 | Moyenne |
| 3554021 | 1 | Faible |
| 3554024 | 2 | Moyenne |
| 3554026 | 1 | Faible |
| 3554029 | 1 | Faible |
| 3554032 | 1 | Faible |
| 3554034 | 2 | Moyenne |
| 3554036 | 2 | Moyenne |
| 3554038 | 1 | Faible |
| 3554042 | 1 | Faible |
| 3554044 | 1 | Faible |
| 3554049 | 1 | Faible |
| 3554052 | 1 | Faible |
| 3554054 | 1 | Faible |
| 3554056 | 1 | Faible |
| 3554057 | 1 | Faible |
| 3554058 | 1 | Faible |
| 3554062 | 2 | Moyenne |
| 3554066 | 2 | Moyenne |
| 3554068 | 2 | Moyenne |
| 3554094 | 1 | Faible |
| 3556014 | 1 | Faible |
| 3556027 | 2 | Moyenne |
| 3556031 | 2 | Moyenne |
| 3556033 | 1 | Faible |
| 3556042 | 1 | Faible |
| 3556048 | 2 | Moyenne |
| 3556052 | 1 | Faible |
| 3556056 | 1 | Faible |
| 3556066 | 2 | Moyenne |
| 3556070 | 2 | Moyenne |
| 3556073 | 1 | Faible |
| 3556076 | 2 | Moyenne |
| 3556077 | 1 | Faible |
| 3556092 | 2 | Moyenne |
| 3556093 | 1 | Faible |
| 3556095 | 1 | Faible |
| 3556098 | 1 | Faible |
| 3556102 | 1 | Faible |
| 3556106 | 1 | Faible |
| 3557001 | 1 | Faible |
| 3557004 | 1 | Faible |
| 3557006 | 1 | Faible |
| 3557008 | 1 | Faible |
| 3557011 | 1 | Faible |
| 3557014 | 1 | Faible |
| 3557016 | 1 | Faible |
| 3557019 | 1 | Faible |
| 3557021 | 1 | Faible |
| 3557026 | 1 | Faible |
| 3557028 | 1 | Faible |
| 3557035 | 1 | Faible |
| 3557038 | 2 | Moyenne |
| 3557039 | 1 | Faible |
| 3557040 | 2 | Moyenne |
| 3557041 | 1 | Faible |
| 3557051 | 1 | Faible |
| 3557061 | 1 | Faible |
| 3557066 | 1 | Faible |
| 3557071 | 1 | Faible |
| 3557072 | 1 | Faible |
| 3557073 | 1 | Faible |
| 3557074 | 1 | Faible |
| 3557076 | 2 | Moyenne |
| 3557078 | 1 | Faible |
| 3557079 | 2 | Moyenne |
| 3557091 | 1 | Faible |
| 3557095 | 1 | Faible |
| 3557096 | 2 | Moyenne |
| 3558001 | 1 | Faible |
| 3558003 | 1 | Faible |
| 3558004 | 1 | Faible |
| 3558011 | 1 | Faible |
| 3558012 | 1 | Faible |
| 3558016 | 1 | Faible |
| 3558019 | 1 | Faible |
| 3558028 | 1 | Faible |
| 3558034 | 1 | Faible |
| 3558041 | 1 | Faible |
| 3558044 | 1 | Faible |
| 3558051 | 1 | Faible |
| 3558054 | 1 | Faible |
| 3558059 | 1 | Faible |
| 3558060 | 1 | Faible |
| 3558061 | 1 | Faible |
| 3558062 | 1 | Faible |
| 3558063 | 1 | Faible |
| 3558064 | 1 | Faible |
| 3558065 | 1 | Faible |
| 3558066 | 1 | Faible |
| 3558067 | 1 | Faible |
| 3558068 | 1 | Faible |
| 3558069 | 1 | Faible |
| 3558075 | 2 | Moyenne |
| 3558076 | 1 | Faible |
| 3558080 | 1 | Faible |
| 3558085 | 1 | Faible |
| 3558090 | 1 | Faible |
| 3558097 | 1 | Faible |
| 3559001 | 1 | Faible |
| 3559011 | 1 | Faible |
| 3559012 | 1 | Faible |
| 3559016 | 1 | Faible |
| 3559019 | 1 | Faible |
| 3559024 | 1 | Faible |
| 3559026 | 1 | Faible |
| 3559031 | 1 | Faible |
| 3559040 | 1 | Faible |
| 3559042 | 1 | Faible |
| 3559047 | 1 | Faible |
| 3559051 | 1 | Faible |
| 3559053 | 1 | Faible |
| 3559060 | 1 | Faible |
| 3559061 | 1 | Faible |
| 3559063 | 1 | Faible |
| 3559064 | 1 | Faible |
| 3559066 | 1 | Faible |
| 3559068 | 1 | Faible |
| 3559069 | 1 | Faible |
| 3559090 | 1 | Faible |
| 3559092 | 1 | Faible |
| 3560001 | 1 | Faible |
| 3560004 | 1 | Faible |
| 3560005 | 1 | Faible |
| 3560008 | 2 | Moyenne |
| 3560010 | 1 | Faible |
| 3560021 | 1 | Faible |
| 3560024 | 1 | Faible |
| 3560027 | 1 | Faible |
| 3560032 | 1 | Faible |
| 3560034 | 1 | Faible |
| 3560042 | 1 | Faible |
| 3560046 | 1 | Faible |
| 3560049 | 1 | Faible |
| 3560050 | 1 | Faible |
| 3560052 | 1 | Faible |
| 3560054 | 1 | Faible |
| 3560055 | 1 | Faible |
| 3560056 | 1 | Faible |
| 3560057 | 1 | Faible |
| 3560058 | 1 | Faible |
| 3560060 | 1 | Faible |
| 3560061 | 1 | Faible |
| 3560063 | 1 | Faible |
| 3560064 | 1 | Faible |
| 3560065 | 1 | Faible |
| 3560066 | 1 | Faible |
| 3560068 | 1 | Faible |
| 3560069 | 1 | Faible |
| 3560070 | 1 | Faible |
| 3560075 | 1 | Faible |
| 3560078 | 1 | Faible |
| 3560080 | 1 | Faible |
| 3560082 | 1 | Faible |
| 3560083 | 1 | Faible |
| 3560084 | 1 | Faible |
| 3560088 | 1 | Faible |
| 3560089 | 1 | Faible |
| 3560090 | 1 | Faible |
| 3560091 | 1 | Faible |
| 3560097 | 1 | Faible |
| 3560104 | 1 | Faible |
- Date de modification :