Analytical Studies Branch Research Paper Series
Do Workplace Pensions Crowd Out Other Retirement Savings? Evidence from Canadian Tax Records
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
by Derek Messacar
Social Analysis and Modelling Division,
Statistics Canada
Abstract
This paper investigates whether registered pension plans (RPPs) help households prepare financially for retirement or simply substitute for other forms of private saving. This issue is addressed using a panel of 1.8 million Canadian households, from 1991 to 2010, which appear in the Longitudinal Administrative Databank. The analysis controls for correlations in savings across accounts due to unobserved tastes for saving by exploiting the fact that employer contribution rates increase discontinuously on earnings above the average industrial wage, a unique feature of occupational pensions in Canada, the effect being estimated in a Regression Kink Design. The results show that: (1) the Canada Pension Plan or Québec Pension Plan contribution rate significantly affects employers’ generosity of RPP provisions; and, (2) RPPs partially crowd out contributions into registered retirement savings plans—by approximately $0.50 per $1.00. The latter finding means that some substitution is occurring between the two plans but that there may still be a role for employer-assisted saving, since one-half of the automatic change in pension wealth passes through into greater total savings. In addition, the crowding-out response is much smaller for workers with weaker histories of saving in retirement accounts. Employer sponsorship and other forms of automatic saving may, therefore, matter a great deal in helping more vulnerable groups save for their retirement.
Executive summary
A large literature in behavioural economics finds that households benefit from assistance with the challenging task of preparing financially for retirement. Workplace pension program characteristics such as default options or savings rate escalators tend to significantly increase contributions to these plans (Madrian and Shea 2001; Choi et al. 2004; Thaler and Benartzi 2004). Recent evidence also suggests that automatic contributions pass through into greater private wealth accumulation even after controlling for possible crowd-out responses in other forms of saving (Gelber 2011; Chetty et al. 2014). These programs are sometimes viewed as effective ways of increasing savings for those who underprepare for retirement, while still allowing active savers to opt out of such arrangements if desired (Thaler and Sunstein 2008; Iwry and John 2009).
However, the effect of workplace pensions on total private savings is still an empirically controversial question. Most of the work on this question analyzes the rapid expansion of 401(k) plans in the United States. Some studies find that workplace pensions do not influence or may even crowd in private wealth accumulation (Poterba, Venti and Wise 1994, 1995; Gelber 2011), whereas others find large displacement effects (Benjamin 2003; Engelhardt and Kumar 2011). The conflicting results may be driven by identification problems that beset this literature (Bernheim 2002) or by different behavioural responses to the types of variation that these studies exploit empirically (noted by Chetty et al. [2014]).
This paper investigates whether an automatic change in registered pension plan (RPP) contributions leads to higher total savings or simply induces a crowd-out response in registered retirement savings plans (RRSP). To control for the possibility that individuals’ contributions across savings accounts are correlated due to unobserved preferences for saving, the analysis exploits a unique feature of RPPs: firms often integrate their contribution formulas with the contribution schedule of the Canada Pension Plan (CPP) or Québec Pension Plan (QPP). That is, many plans (80% to 85%) have lower marginal contribution rates for income levels that are charged more heavily by the CPP or QPP, and vice versa. This occurs because firms realize the additional costs imposed on them by the public pension and commensurately reduce their payments to RPPs (Frenken 1996). As a result, workers’ savings in RPPs change at the earnings threshold associated with a change in the CPP or QPP contribution rate through no control of their own. Using regression techniques, the effect of this savings rate change on RPP contributions is estimated, as is the resulting displacement effect on RRSPs. Therefore, this paper offers new insight into the role of RPPs in helping households save for retirement, while improving upon some of the methodological issues prevalent in related studies.
The results show that RRSP contributions decrease by approximately $0.50 per $1.00 increase in RPPs, for workers with: (1) strictly positive savings in both accounts; and (2) total tax-deductible savings strictly below their RRSP contribution limits. On balance, some behavioural substitution is occurring between the two plans, but there may still be a role for employer-assisted saving given that one-half of the automatic change in pension wealth passes through into greater total savings. Moreover, the response tends to be smaller for workers with weaker histories of saving in retirement accounts. Employer sponsorship and other forms of automatic saving may, therefore, matter a great deal in helping more vulnerable groups save for their retirement.
1 Introduction
The extent to which employer-sponsored pension plans help households prepare financially for retirement is both a theoretically and empirically controversial question. The standard economic model predicts that forward-looking households may compensate for changes in workplace pensions by adjusting asset balances in other retirement accounts. Yet a large literature in behavioural economics finds that households also benefit from assistance with the difficult task of saving for retirement in ways that are not explained by rational agency. Pension program characteristics such as default options or savings rate escalators tend to significantly increase contributions to these plans (Madrian and Shea 2001; Choi et al. 2004; Thaler and Benartzi 2004). Recent evidence also suggests that automatic contributions pass through into greater private wealth accumulation even after controlling for possible crowd-out responses in other forms of saving (Gelber 2011; Chetty et al. 2014). These programs are therefore viewed as effective ways of increasing savings for those who under-prepare for retirement, while still allowing active savers to opt out of such arrangements if desired (Thaler and Sunstein 2008; Iwry and John 2009).
This paper investigates whether an automatic change in registered pension plan (RPP) contributions leads to higher total savings or simply induces individuals to reduce savings in registered retirement savings plans (RRSPs). The Longitudinal Administrative Databank (LAD) is used to obtain accurate information on the savings behaviour of a large sample of Canadians. To control for the possibility that individuals’ contributions across savings accounts are correlated due to unobserved preferences for saving, the analysis exploits a unique feature of RPPs: firms often integrate their contribution formulas with the contribution schedule of the Canada Pension Plan (CPP) and Québec Pension Plan (QPP). That is, many plans (80% to 85%) have lower marginal contribution rates for income levels that are charged more heavily by the CPP or QPP, and vice versa. This occurs because firms realize the additional costs imposed on them by the public pension and commensurately reduce their payments to RPPs (Frenken 1996). As a result, workers’ savings in RPPs change at the earnings threshold associated with a change in the CPP or QPP contribution rate through no control of their own. Using regression techniques, the effect of this savings rate change on RPP contributions is estimated, as is the resulting displacement effect on RRSPs.
The findings show that RRSP contributions decrease by approximately $0.50 per $1.00 increase in RPPs, for workers with: (1) strictly positive savings in both accounts; and (2) total tax-deductible savings strictly below their RRSP contribution limits. On balance, some behavioural substitution is occurring between the two plans, but there may still be a role for employer-assisted saving given that one-half of the automatic change in pension wealth passes through into greater total savings. A closer inspection shows that the crowd-out response also tends to be much smaller for workers with weaker histories of saving in retirement accounts. Employer sponsorship and other forms of automatic saving may, therefore, matter a great deal in helping more vulnerable groups save for their retirement.
This paper is organized as follows. The next section gives a review of the literature to help motivate the study. Then, Section 3 outlines Canada’s retirement income system to provide a context in which to interpret the results. Section 4 describes the data and sample selection, and Section 5 discusses the empirical strategy used to identify the crowding-out effect of RPPs. Section 6 presents the main results, robustness checks, and tests of heterogeneous responses for different types of savers. Finally, the last section concludes.
2 Literature review
Previous empirical research on the effects of workplace pensions has not reached a consensus. Most of this work analyzes the rapid expansion of 401(k) plans in the United States. Poterba, Venti and Wise (1994, 1995) compare the financial assets of workers who are, or are not, eligible for 401(k)s according to whether or not their employers offer such plans. The authors show that 401(k) contributions do not crowd out assets in other accounts. Venti and Wise (1996) reach the same conclusion by comparing workers from different cohorts who, in turn, had different lengths of exposure to 401(k)s during their careers. Gelber (2011) exploits a change in 401(k) eligibility that arises when an employee has worked at a firm long enough, and shows that these plans may crowd in individual retirement account (IRA) contributions but that they have no effect on other financial assets.
In contrast, Engen, Gale and Scholz (1994, 1996) find that 401(k) eligibility does not boost private saving when comparing asset patterns of plan participants to those of non-participants who hold IRAs. Gale (1998) finds large displacement effects of 401(k)s on net worth using a broader definition of wealth. In addition, evidence of the effects of workplace pensions in other countries is also mixed. For example, Veall (2001) finds that Canadians’ savings levels in registered retirement savings plans (RRSPs) significantly decrease as workers move into registered pension plan (RPP) coverage, although Milligan (2002) notes that RPP members are still more likely than non-members to make RRSP contributions. Alessie, Kapteyn and Klijn (1997) find that occupational pensions raise total savings in the Netherlands, but Euwals (2000) reaches the opposite conclusion. Chetty et al. (2014) look at changes in savings for workers who move between firms with varying degrees of pension benefit generosity in Denmark and find that contributions to these plans tend to pass through into higher total saving for most workers.
These studies all contribute to our understanding of how workplace pensions affect private savings outcomes. However, several identification problems also beset this literature (Hubbard and Skinner 1996; Bernheim 2002). First, measurement error in reported pension wealth from survey data may cause researchers to overstate the extent to which workplace plans generate new savings (Engelhardt and Kumar 2011). Second, unobserved heterogeneity in individuals’ tastes for saving would introduce upward bias in ordinary least squares estimates of crowd-out, because some individuals tend to save more in all types of accounts, including employer-sponsored plans. Third, workers may sort into firms based on pension coverage, which would introduce bias in comparisons of savings outcomes between eligible and ineligible members (Ippolito 1997). Firms may also choose to offer pensions based on the demands of their workers. Fourth, studies that find that changes in workplace savings do not induce behavioural crowd-out responses must contend with the possibility that workers were simply unaware of such changes, as people often know very little about the details of their occupational pensions (Mitchell 1988; Luchak and Gunderson 2000).
The impact of workplace pensions on wealth accumulation remains unclear, despite such extensive efforts, in large part because of the lack of suitable research designs (Bernheim 2002). This paper aims to provide new insight into this important question while addressing these methodological issues.
3 Overview of Canada’s retirement income system
This section provides a brief overview of Canada’s retirement income system, which comprises three pillars: (1) the Old Age Security (OAS) program; (2) the Canada Pension Plan (CPP) and Québec Pension Plan (QPP); and (3) private pensions and retirement savings plans. Although this study focuses on the interaction of two savings plans both belonging to the third pillar, a review of the full system provides a proper context for interpreting the results.
3.1 The Old Age Security program
The OAS program comprises an OAS pension, a Guaranteed Income Supplement (GIS), and an allowance. Together, these benefits represent the Government of Canada’s largest pension program. It is funded by general tax revenues, and individuals do not contribute directly into it.
The OAS pension is a benefit for most Canadians aged 65 or older who satisfy legal status and residency requirements. The maximum monthly payment for these individuals was $522 in December 2010. Benefits are linked to inflation to reflect increases in the cost of living and are fully taxable. For low-income OAS recipients, the GIS provides an income-tested, non-taxable supplemental benefit. In December 2010, the maximum monthly support provided through GIS was $658 for singles and $435 per person for couples. Finally, the allowance is an income-tested benefit available to 60- to 64-year-old partners of OAS recipients, as well as their widows or widowers. This benefit is equal to the OAS pension plus the GIS at the married or widowed rate, as applicable. The reader may wish to refer to Baker, Gruber and Milligan (2007) for more information.
3.2 The Canada Pension Plan and Québec Pension Plan
The CPP and the QPP are contributory, income-tested public pensions funded through matching employer and employee payroll deductions. While minor differences between the plans exist, they are sufficiently similar for the purpose of this study to be referred to jointly as the CPP or QPP.
The base for the CPP or QPP payroll deductions is the earnings between a Year’s Basic Exemption (YBE) and a Year’s Maximum Pensionable Earnings (YMPE) amount. Every person in Canada between the ages of 18 and 70 earning a salary above the YBE is required to contribute to the CPP or QPP. Table 1 shows the annual contribution rates as well as the YBE and YMPE from 1991 to 2010. For example, paid workers and their employers each contributed 4.95% of earnings between $3,500 and $47,200 in 2010. Self-employed workers are required to pay both shares of contributions up to the maximum. The YBE has been frozen at $3,500 for some time but the YMPE is indexed to the average industrial wage. The marginal contribution on earnings beyond this amount is zero.
The CPP or QPP is designed to replace approximately 25% of workers’ average lifetime earnings, up to the average industrial wage. Actual pension benefits are calculated using a process that depends on workers’ earnings histories, the length of time spent contributing, and the age at which benefits start to be collected. The normal retirement age in the CPP or QPP is 65 but workers may start to collect reduced benefits as early as age 60. The benefit calculation also incorporates time spent caring for children, time in which workers were eligible for disability benefits, and several other factors to mitigate the impact of low-income years on entitlements. In 2010, the maximum monthly CPP or QPP retirement pension amount was $934.
| Year | Year's Basic Exemption | Year's Maximum Pensionable Earnings | Contribution rate | Maximum annual contribution |
|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | |
| dollars | dollars | percent | dollars | |
| 1991 | 3,000 | 30,500 | 2.40 | 660 |
| 1992 | 3,200 | 32,200 | 2.50 | 725 |
| 1993 | 3,200 | 33,400 | 2.60 | 785 |
| 1994 | 3,400 | 34,400 | 2.70 | 837 |
| 1995 | 3,400 | 34,900 | 2.80 | 882 |
| 1996 | 3,500 | 35,400 | 2.90 | 925 |
| 1997 | 3,500 | 35,800 | 3.00 | 969 |
| 1998 | 3,500 | 36,900 | 3.20 | 1,069 |
| 1999 | 3,500 | 37,400 | 3.50 | 1,187 |
| 2000 | 3,500 | 37,600 | 3.90 | 1,330 |
| 2001 | 3,500 | 38,300 | 4.30 | 1,496 |
| 2002 | 3,500 | 39,100 | 4.70 | 1,673 |
| 2003 | 3,500 | 39,900 | 4.95 | 1,802 |
| 2004 | 3,500 | 40,500 | 4.95 | 1,832 |
| 2005 | 3,500 | 41,100 | 4.95 | 1,861 |
| 2006 | 3,500 | 42,100 | 4.95 | 1,911 |
| 2007 | 3,500 | 43,700 | 4.95 | 1,990 |
| 2008 | 3,500 | 44,900 | 4.95 | 2,049 |
| 2009 | 3,500 | 46,300 | 4.95 | 2,119 |
| 2010 | 3,500 | 47,200 | 4.95 | 2,163 |
|
Note: Both employers and employees pay into the Canada Pension Plan or Québec Pension Plan up to the maximum annual contribution; self-employed workers are required to pay both shares. See text for further discussion. Columns 1 to 3 report institutional parameters. Column 4 is calculated as [Column 2 - Column 1] × Column 3. Sources: Canada Revenue Agency, Canada Pension Plan regulations; and Revenu Québec, Québec Pension Plan regulations. |
||||
3.3 Private pensions and retirement savings plans
The third pillar of the retirement income system consists of savings in private pensions and retirement savings accounts, which are described in turn.
3.3.1 Registered pension plans
Registered pension plans (RPPs) are arrangements with employers to provide pensions to retired employees in the form of periodic payments. These arrangements may either be defined-benefit or defined-contribution plans. For defined-contribution RPPs, employers are required to contribute a minimum of 1% of the total pensionable earnings (compensation) paid to all active plan members. For defined-benefit RPPs, employers are generally required to finance 50% of the cost of the benefits. Employees in both defined-contribution and defined-benefit RPPs also typically contribute (nearly 75% of RPP members make contributions, as shown in Table 2). RPP savings are tax-deferred: contributions are tax-deductible; investment income is not taxed as it is earned in the plan, and pension payments are included in income for tax purposes. Contributions to defined-contribution RPPs are limited to 18% of earnings up to a specified dollar amount ($22,450 in 2010). Benefits provided under a defined-benefit RPP are limited to 2% of earnings per year of service up to a specified dollar amount ($2,494 in 2010).
For the sample of frequent tax filers used in this study, Table 2 shows a comparison of demographics, earnings, and savings characteristics of RPP members and non-members. RPP members are more likely to be male, to work in public administration and to be unionized, but are less likely to have self-employment income or to collect Employment Insurance (EI). Also, they tend to have higher employment and total income but earn less from investments and capital gains. Most notably, the median savings rate for RPP members (including any registered retirement savings plan [RRSP] saving) is 4.7 percentage points higher than those not participating in an RPP.
3.3.2 Registered retirement savings plans
RRSPs are individual, defined-contribution plans generally set up through financial institutions (note that an employer may establish a group RRSP for its employees, which is a collection of individual employee RRSPs administered by a single RRSP issuer). Savings in RRSPs, like those in an RPP, receive a deferral of tax. RRSP contributions are limited to 18% of prior year earned income up to a specified dollar amount ($22,000 in 2010) minus any pension adjustment for RPP members (which reflects the estimated amount of employer and employee RPP contributions for the prior year), plus any unused RRSP room carried forward from previous years. This approach effectively integrates the RPP and RRSP limits by ensuring that RPP members’ annual RPP savings are taken into account in determining their RRSP limits.
| RPP members | RPP non-members | |||
|---|---|---|---|---|
| Average | Median | Average | Median | |
| Column 1 | Column 2 | Column 3 | Column 4 | |
| years | ||||
| Demographics | ||||
| Age | 44.3 | Note ...: not applicable | 44.0 | Note ...: not applicable |
| percent | ||||
| Female | 48.6 | Note ...: not applicable | 56.2 | Note ...: not applicable |
| Male | 51.4 | Note ...: not applicable | 43.8 | Note ...: not applicable |
| Married | 79.1 | Note ...: not applicable | 77.2 | Note ...: not applicable |
| Employment | ||||
| Employed | 100.0 | Note ...: not applicable | 64.3 | Note ...: not applicable |
| Self-employed | 2.8 | Note ...: not applicable | 14.9 | Note ...: not applicable |
| Public administration | 9.0 | Note ...: not applicable | 1.0 | Note ...: not applicable |
| Unionized | 67.3 | Note ...: not applicable | 12.7 | Note ...: not applicable |
| Employment Insurance recipient | 11.5 | Note ...: not applicable | 16.3 | Note ...: not applicable |
| nominal dollars | ||||
| Conditional income | ||||
| Gross employment income | 46,400 | 43,700 | 27,400 | 22,300 |
| Net self-employment income | 950 | -450 | 17,250 | 8,800 |
| Net investment income | 700 | 200 | 1,050 | 300 |
| Net capital gains | 1,100 | 300 | 1,500 | 400 |
| Gross total income | 48,450 | 45,250 | 27,400 | 20,800 |
| percent | ||||
| Savings participation | ||||
| RPP members (PA) | 100.0 | Note ...: not applicable | 0.0 | Note ...: not applicable |
| RPP employee contributors | 74.6 | Note ...: not applicable | 0.0 | Note ...: not applicable |
| RRSP contributors | 53.7 | Note ...: not applicable | 29.3 | Note ...: not applicable |
| RRSP withdrawers | 6.8 | Note ...: not applicable | 6.0 | Note ...: not applicable |
| Unused RRSP room | 88.3 | Note ...: not applicable | 83.2 | Note ...: not applicable |
| nominal dollars | ||||
| Conditional savings | ||||
| RPP contributions (PA) | 4,500 | 3,950 | 0 | 0 |
| RPP employee contributions | 2,150 | 1,900 | 0 | 0 |
| Gross RRSP contributions | 3,200 | 2,400 | 4,450 | 3,000 |
| RRSP withdrawals | 2,450 | 1,350 | 2,850 | 1,750 |
| Unused RRSP room | 21,500 | 15,400 | 21,500 | 12,950 |
| Conditional total savings | ||||
| Savings | 6,050 | 5,250 | 3,450 | 2,150 |
| percent | ||||
| Savings rate | 16.1 | 11.6 | 5.8 | 6.9 |
|
... not applicable Note: The ‘conditional’ statistics are restricted to strictly positive values of saving or withdrawing. The savings rate is calculated as total net tax-deductible savings relative to total income. Total net tax-deductible savings is defined as registered pension plan (RPP) savings (measured by the pension adjustment [PA]) plus registered retirement savings plan (RRSP) contributions less withdrawals. Total income is a constructed measure that includes income from various sources such as employment (e.g., employment and self-employment earnings), other types of income (e.g., dividends, interest and investment income, net rental income), and transfers or credits (e.g., employment insurance, social assistance), as described in more detail in the Longitudinal Administrative Databank Data Dictionary. Information on sector of employment is only available from 2000 onward. The values shown here correspond to those of the particular cohort used in the upcoming empirical analysis for the years 1991 to 2010 inclusive. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||
Table 3 shows that, for individuals with unused RRSP contribution room (defined as the difference between the total room available in the reference year and the amount contributed in that same year), the unused contribution room increases significantly with age. Although the proportion of savers with unused room decreases slightly, perhaps because savings rates tend to rise over the life cycle, the fact remains that the majority of tax filers (at least 80%) have unused RRSP contribution room irrespective of their age.
| Percentage > 0 | Average | |
|---|---|---|
| Column 1 | Column 2 | |
| percent | nominal dollars | |
| Registered pension plan | ||
| Ages 25 to 34 | 30.9 | 3,000 |
| Ages 35 to 44 | 37.3 | 4,250 |
| Ages 45 to 54 | 39.8 | 5,000 |
| Ages 55 and over | 31.1 | 5,200 |
| Net registered retirement savings plan | ||
| Ages 25 to 34 | 31.5 | 2,850 |
| Ages 35 to 44 | 38.2 | 3,650 |
| Ages 45 to 54 | 41.1 | 4,050 |
| Ages 55 and over | 37.0 | 4,750 |
| Unused registered retirement savings plan contribution room | ||
| Ages 25 to 34 | 87.0 | 9,350 |
| Ages 35 to 44 | 86.2 | 19,450 |
| Ages 45 to 54 | 84.2 | 26,450 |
| Ages 55 and over | 81.9 | 31,450 |
|
Note: Column 1 shows the percentage of individuals in the sample with each characteristic. Column 2 shows the average amount conditional on that amount being strictly positive. The values shown here correspond to those of the particular cohort used in the upcoming empirical analysis for the years 1991 to 2010 inclusive. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||
4 Data and sample selection
The Longitudinal Administrative Databank (LAD) is used to carry out this research study. The LAD is a panel data file comprising a 20% sample of the annual T1 Family File and the Longitudinal Immigration Database. In addition, the sample is augmented annually to ensure accurate cross-sectional representation. The file contains many variables about the demographics, incomes, taxes, allowances, receipts, transfers, and savings characteristics of the represented individuals and their census families.
The following sample restrictions are imposed. First, the sample is restricted to the years 1991 to 2010, which is the period from the first year that data on workplace pension coverage became available to the last year of data availability. Second, the analysis applies to individuals born during the 1942-to-1966 period, meaning they were aged from 25 to 51 in 1991 (from 44 to 68 in 2010). The upper age limit of 68 was chosen because individuals were required to start receiving a pension from their registered pension plans (RPPs) by the time they turned 69 years of age over the period from 1997 to 2006 (this was increased to 71 years of age in 2007). Third, only the individuals of the selected cohort who are observed filing taxes in at least 18 of the 20 years are included. In all, 73.6% of the selected cohort is observed at least 90% of the time. These restrictions result in a sample of approximately 34 million observations on 1.8 million tax filers. In the analysis, adjustments are made for outliers, and individuals are only included during the years in which they are not observed collecting public or private pension income so as to focus on savings decisions before retirement.
A limitation of the LAD is that it does not provide direct information on individuals’ RPP coverage status or contribution levels. The pension adjustment (PA) variable is used as a proxy for RPP contributions. The PA reflects the value of the pension benefits earned annually under workplace pensions and deferred profit-sharing plans (DPSPs). The PA was created in 1991 (and appears in the LAD since then, as well) as a way of ensuring that RPP members and non-members receive equal tax treatment of tax-assisted savings. Specifically, the current-year PA is used to reduce the next-year RRSP contribution room commensurately.
The inclusion of DPSPs in the PA likely results in a modest over-estimation of RPP coverage; for example, members of DPSPs accounted for 7% of RPP members in 1993 (Ostrovsky and Schellenberg 2009). While the LAD also includes separate information on employee contributions to RPPs since 1986, it would not capture information on employer-only contribution plans. Morissette and Ostrovsky (2006) show that, in 1991, using the variable on employee RPP contributions as an indicator for coverage would result in an under-estimation of coverage of 17 percentage points for married men aged 35 to 54 and of 11 percentage points for married women aged 35 to 54. Therefore, the convention of using the PA as a proxy for RPP coverage is followed. For this analysis, the exogenous variation in the PA that the empirical methodology exploits (described in Subsection 5.1, below) works entirely through RPP contributions, and the fact that DPSPs are also included in the PA is not expected to bias the estimator in any way.
5 Methodology
This section begins by describing the source of exogenous variation in registered pension plan (RPP) contributions and the identification strategy used in the study. Next, the underlying assumptions of the empirical method are discussed, and some evidence in support of these assumptions is given. Finally, two limitations of the identification strategy are addressed.
5.1 Exogenous variation in registered pension plan contributions
The analysis exploits a change in RPP savings that arises from the fact that most employers integrate their contribution formulas with the contribution schedule of the Canada Pension Plan and the Québec Pension Plan (QPP). The CPP and QPP, introduced in 1966, are partially funded through employer payroll deductions and therefore impose additional pension costs on employers already sponsoring occupational plans. This reform induced many employers to amend their plans in recognition of these other costs and the fact that the public pension somewhat duplicates employer-sponsored coverage (Frenken 1996). The integration feature has persisted over the last 50 years (Statistics Canada 2003, p. 65); in 1994, for example, 80% of RPP members had integrated contributions or benefits (Statistics Canada 1996, p. 64).
The most common method of integration is the step-rate method, which uses two contribution and benefit rates, typically for earnings below or above the Year’s Maximum Pensionable Earnings (YMPE) threshold. For example, “the pension per year of service may be 1.3% of earnings up to the YMPE and 2.0% of earnings over the YMPE, with members being able to make contributions of 4.8% of their earnings up to the YMPE and 7.5% of earnings above it” (Statistics Canada 2003, p. 65). The employee’s share of RPP contributions may also be integrated, either mandatorily or because firms allow for higher marginal savings rates on earnings above the threshold (see Frenken [1996, p. 67] and Statistics Canada [2003, p. 65] for examples). For defined-benefit plans, the same principle applies: integrated RPPs offer lower rates of benefit accrual on earnings up to the CPP or QPP maximum than on earnings above that level (Baldwin 2007, p. 7). A less common method of integration is the offset method, in which contributions and benefits are reduced by all or part of the contributions into, or benefits from, the CPP or QPP.
Integration results in an RPP contribution schedule as a function of earnings that kinks upward at the threshold associated with the YMPE. To illustrate this point, Chart 1 plots the CPP or QPP contribution schedule for employment income below $50,000 using the 1991 parameters, as specified in Table 1. The marginal contribution rate is 2.4% on earnings between the Year’s Basic Exemption (YBE) ($3,000 in 1991) and the YMPE ($30,500 in 1991) but then falls to zero on higher earnings. The chart also plots a hypothetical RPP contribution schedule, where the savings rate is 3% on earnings below the YMPE and 5% thereafter. As a result, the combined contributions to both pensions remain relatively constant. However, the change in the CPP or QPP contribution does not imply a change in retirement wealth, given that CPP or QPP benefits are a complex function of lifetime earnings and are independent of the actual amounts paid into the plan during working years. In contrast, the kink in RPP contributions directly affects retirement wealth. By design, this change is uncorrelated with individuals’ preferences for saving because it arises from employers’ decisions of whether or not to integrate. It is inferred that most RPP members sampled receive the treatment, given that the vast majority of plans are integrated.

Description for chart 1
The title of the graph is "Chart 1 Hypothetical CPP or QPP and RPP contribution schedules for 1991."
This is a line chart.
There are in total 101 categories in the horizontal axis. The vertical axis starts at 0 and ends at 2,000 with ticks every 500 points.
There are 2 series in this graph.
The vertical axis is "Contributions
(nominal dollars)."
The horizontal axis is "Employment income (dollars)."
The title of series 1 is "CPP or QPP payment."
The minimum value is 0 and it corresponds to "0, 500, 1000, 1500, 2000, 2500 and 3000."
The maximum value is 660 and it corresponds to "30,500, 31,000, 31,500, 32,000, 32,500, 33,000, 33,500, 34,000, 34,500, 35,000, 35,500, 36,000, 36,500, 37,000, 37,500, 38,000, 38,500, 39,000, 39,500, 40,000, 40,500, 41,000, 41,500, 42,000, 42,500, 43,000, 43,500, 44,000, 44,500, 45,000, 45,500, 46,000, 46,500, 47,000, 47,500, 48,000, 48,500, 49,000, 49,500 and 50,000."
The title of series 2 is "RPP contribution."
The minimum value is 0 and it corresponds to "0."
The maximum value is 1,890 and it corresponds to "50,000."
| CPP or QPP payment | RPP contribution | |
|---|---|---|
| 0 | 0 | 0 |
| 500 | 0 | 15 |
| 1,000 | 0 | 30 |
| 1,500 | 0 | 45 |
| 2,000 | 0 | 60 |
| 2,500 | 0 | 75 |
| 3,000 | 0 | 90 |
| 3,500 | 12 | 105 |
| 4,000 | 24 | 120 |
| 4,500 | 36 | 135 |
| 5,000 | 48 | 150 |
| 5,500 | 60 | 165 |
| 6,000 | 72 | 180 |
| 6,500 | 84 | 195 |
| 7,000 | 96 | 210 |
| 7,500 | 108 | 225 |
| 8,000 | 120 | 240 |
| 8,500 | 132 | 255 |
| 9,000 | 144 | 270 |
| 9,500 | 156 | 285 |
| 10,000 | 168 | 300 |
| 10,500 | 180 | 315 |
| 11,000 | 192 | 330 |
| 11,500 | 204 | 345 |
| 12,000 | 216 | 360 |
| 12,500 | 228 | 375 |
| 13,000 | 240 | 390 |
| 13,500 | 252 | 405 |
| 14,000 | 264 | 420 |
| 14,500 | 276 | 435 |
| 15,000 | 288 | 450 |
| 15,500 | 300 | 465 |
| 16,000 | 312 | 480 |
| 16,500 | 324 | 495 |
| 17,000 | 336 | 510 |
| 17,500 | 348 | 525 |
| 18,000 | 360 | 540 |
| 18,500 | 372 | 555 |
| 19,000 | 384 | 570 |
| 19,500 | 396 | 585 |
| 20,000 | 408 | 600 |
| 20,500 | 420 | 615 |
| 21,000 | 432 | 630 |
| 21,500 | 444 | 645 |
| 22,000 | 456 | 660 |
| 22,500 | 468 | 675 |
| 23,000 | 480 | 690 |
| 23,500 | 492 | 705 |
| 24,000 | 504 | 720 |
| 24,500 | 516 | 735 |
| 25,000 | 528 | 750 |
| 25,500 | 540 | 765 |
| 26,000 | 552 | 780 |
| 26,500 | 564 | 795 |
| 27,000 | 576 | 810 |
| 27,500 | 588 | 825 |
| 28,000 | 600 | 840 |
| 28,500 | 612 | 855 |
| 29,000 | 624 | 870 |
| 29,500 | 636 | 885 |
| 30,000 | 648 | 900 |
| 30,500 | 660 | 915 |
| 31,000 | 660 | 940 |
| 31,500 | 660 | 965 |
| 32,000 | 660 | 990 |
| 32,500 | 660 | 1,015 |
| 33,000 | 660 | 1,040 |
| 33,500 | 660 | 1,065 |
| 34,000 | 660 | 1,090 |
| 34,500 | 660 | 1,115 |
| 35,000 | 660 | 1,140 |
| 35,500 | 660 | 1,165 |
| 36,000 | 660 | 1,190 |
| 36,500 | 660 | 1,215 |
| 37,000 | 660 | 1,240 |
| 37,500 | 660 | 1,265 |
| 38,000 | 660 | 1,290 |
| 38,500 | 660 | 1,315 |
| 39,000 | 660 | 1,340 |
| 39,500 | 660 | 1,365 |
| 40,000 | 660 | 1,390 |
| 40,500 | 660 | 1,415 |
| 41,000 | 660 | 1,440 |
| 41,500 | 660 | 1,465 |
| 42,000 | 660 | 1,490 |
| 42,500 | 660 | 1,515 |
| 43,000 | 660 | 1,540 |
| 43,500 | 660 | 1,565 |
| 44,000 | 660 | 1,590 |
| 44,500 | 660 | 1,615 |
| 45,000 | 660 | 1,640 |
| 45,500 | 660 | 1,665 |
| 46,000 | 660 | 1,690 |
| 46,500 | 660 | 1,715 |
| 47,000 | 660 | 1,740 |
| 47,500 | 660 | 1,765 |
| 48,000 | 660 | 1,790 |
| 48,500 | 660 | 1,815 |
| 49,000 | 660 | 1,840 |
| 49,500 | 660 | 1,865 |
| 50,000 | 660 | 1,890 |
|
Note: The Canada Pension Plan (CPP) or Québec Pension Plan (QPP) contribution schedule is plotted using the relevant tax parameters for the year 1991. RPP: registered pension plan. Source: Statistics Canada, author's calculations based on data from the Canada Revenue Agency (Canada Pension Plan regulations) and Revenu Québec (Québec Pension Plan regulations). |
||
5.2 Identification strategy
The Regression Kink Design (RKD) is used to estimate the changes in RPP and registered retirement savings plan (RRSP) contributions at the earnings level coinciding with the YMPE threshold. Formally, the statistical estimating equations are:
conditional on . Here, denotes individual ’s employment income relative to the average industrial wage in year and are polynomial functions, is a vector of individual-specific covariates observed in the data, and is an indicator of whether income exceeds the YMPE threshold in year . One-year lagged earnings and RPP contributions are used, given that the current year’s pension adjustment (PA) determines the next year’s RRSP contribution room. The parameter is the bandwidth size used to estimate the local average treatment effect. The analysis is restricted to individuals with strictly positive RPP and RRSP savings in the baseline model.
Equation (1) captures the ‘first-stage’ effect of integration on RPP contributions. The parameter of interest , captures the change in the slope of RPP contributions as a function of earnings. Intuitively, the RKD estimates the effect of integration on RPP contributions using a cross-sectional strategy for a group of workers with employment income localized around the threshold. The strategy assumes that individuals on one side of the kink are an appropriate control group for individuals on the other side, at least within a reasonable distance (bandwidth). Because most RPPs have larger savings rates beyond the threshold, as discussed above, the expectation is that . Similarly, Equation (2) captures the ‘second-stage’ RRSP savings response to the change in RPP contributions, where crowd-out predicts .
The overall effect of RPP contributions on RRSP saving is given by the ratio . Both equations are estimated simultaneously using the seemingly unrelated regression (SUR) framework, and standard errors are obtained for the crowd-out parameter using the Delta method. Standard errors are clustered at the individual level to account for unit-specific correlations of the residuals, as recommended by Lee and Lemieux (2010).
5.3 Test of validity
Because integration is decided at the level of the firm, changes in RPP contributions around the YMPE threshold represent a plausibly exogenous source of variation with which to identify the resulting displacement effects on RRSP contributions. This assumes, however, that employment income around the threshold is as good as randomly assigned. The method is invalid if workers have some control over their income levels relative to the kink, because the estimates of treatment would capture a weighted average of the effect of integration and a sorting response.
Figure 1 tests for sorting around the threshold by plotting the distribution of employment income in the reference year relative to the YMPE in that year; the McCrary discontinuity test is used to determine if any observed sorting is statistically significant. The full sample chart in Figure 1 shows that a sorting response is detected, which suggests either workers or employers may be responding directly to the CPP or QPP contribution in setting employment levels. However, the remaining three charts in Figure 1 show that most of the sorting response is driven by workers who are not covered by occupational pensions and who do not belong to unions (recall, the majority of RPP members are also unionized). Wages and salaries for unionized workers are often determined at the group level, which would make sorting more difficult at the individual level. The difficulty of sorting at the individual level is especially true given that, as Table 1 showed, the YMPE threshold has changed annually as a result of its linkage to the average industrial wage. Overall, there is no evidence of sorting for RPP members that would call into question the validity of using the RKD strategy.
5.4 Salience of the treatment effect
The PA helps to rule out concerns that changes in RPP savings may pass through into higher total savings simply because workers were unaware of the changes. The PA is reported transparently to RRSP account holders by the Canada Revenue Agency on their RRSP deduction limit statements and is used directly in calculating individuals’ contribution room for the next year. Thus, workers need not have a deep understanding of how their pension benefits are determined to know approximately how much they saved in their plans in a given year. This helps ensure that workers have enough information about their RPP savings when making RRSP contribution and withdrawal decisions to behave as if the change in their RPP savings caused by integration were salient, even though they may not be directly aware of this plan characteristic.
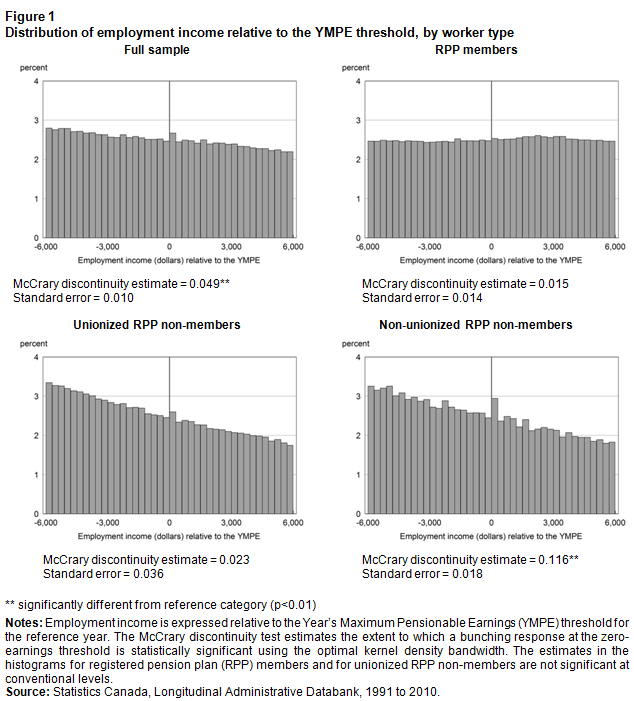
Description for figure 1
The title of the figure is “Distribution of employment income relative to the YMPE threshold, by worker type.”
This figure contains four charts which are described below. The charts represent histograms of employment income for the four following groups: full sample, registered pension plan (RPP) members, unionized RPP non-members and non-unionized RPP non-members.
Chart title: Full sample
This is a bar chart.
The vertical axis (y-axis) is “percent,” beginning at 0 and ending at 4.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at -6,000 and ending at 6,000.
The histogram for the full sample plots the distribution of employment income relative to the Year’s Maximum Pensionable Earnings (YMPE) threshold in the reference year. The sample is all workers with positive earnings between $6,000 on either side of the YMPE threshold. The earnings bins are in widths of $300. The distribution is slightly downward-sloping, from about 2.8% mass at earnings of $6,000 to the left of the threshold down to about 2.2% mass at earnings of $6,000 to the right. The distribution also shows a small spike in the mass of individuals earning very close to the zero-earnings limit. This suggests there may be a sorting response to the Canada Pension Plan or Québec Pension Plan contribution and/or benefit schedule. The McCrary discontinuity test statistic for this histogram, which gives an estimate of the extent to which bunching is detected, is 0.049. The result is significant at the 1% level. The standard error is 0.010.
Chart title: RPP members
This is a bar chart.
The vertical axis (y-axis) is “percent,” beginning at 0 and ending at 4.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at -6,000 and ending at 6,000.
The histogram for RPP members plots the distribution of relative employment income for RPP members. The distribution is relatively uniform at around 2.5% mass, per bin. No discernible spike is observed. The McCrary discontinuity test statistic is 0.015. The standard error is 0.014.
Chart title: Unionized RPP non-members
This is a bar chart.
The vertical axis (y-axis) is “percent,” beginning at 0 and ending at 4.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE” beginning at -6,000 and ending at 6,000.
The histogram for unionized RPP non-members plots the distribution of relative employment income for RPP non-members who belong to unions. The distribution is downward-sloping, from about 3.3% mass at earnings of $6,000 to the left of the threshold down to about 1.8% mass at earnings of $6,000 to the right. No discernible spike is observed. The McCrary discontinuity test statistic is 0.023. The standard error is 0.036.
Chart title: Non-unionized RPP non-members
This is a bar chart.
The vertical axis (y-axis) is “percent,” beginning at 0 and ending at 4.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at -6,000 and ending at 6,000.
The histogram for non-unionized RPP non-members plots the distribution of relative employment income for RPP non-members who do not belong to unions. The distribution closely resembles the one shown in the histogram for unionized RPP non-members. However, a large spike in the distribution is observed at the threshold, which suggests the majority of the bunching response observed in the full sample results through this group. The McCrary discontinuity test statistic is 0.116. It is significant at the 1% level. The standard error is 0.018.
Also, although the Longitudinal Administrative Databank does not identify whether individuals belong to defined-benefit or defined-contribution plans, the PA helps ensure that members of all plan types are affected similarly by integration. For defined-contribution RPPs, the PA is simply the sum of employer and employee contributions into the plans in the reference year. For defined-benefit plans, the PA translates the yearly-accrued pension benefit into a dollar equivalent. That is, it is an estimate of the contribution required to finance the annual benefit accrual, using a career average pension cost factor that is based on a set of long-term economic assumptions and several actuarial assumptions.
6 Results
This section begins with a graphical inspection of how workplace and non-workplace retirement savings behaviour responds around the Canada Pension Plan (CPP) or Québec Pension Plan (QPP) earnings threshold. Then, the detailed regression results, robustness checks, and extensions are presented. The last subsection investigates heterogeneous responses for different types of savers.
The analysis conditions on workers with strictly positive savings in both registered pension plans (RPPs) and registered retirement savings plans (RRSPs) in the reference year, unless otherwise stated, in order to focus on individuals for whom substitution is possible. It is important to note that only approximately 50% of RPP members also contribute into RRSPs in a given year. These workers tend to have higher average employment earnings ($51,350 compared to $40,650) and total income ($53,650 compared to $42,450), are less likely to be unionized (63.5% compared to 71.8%) or to collect employment insurance (8.3% compared to 15.2%), and are slightly less likely to make RPP employee contributions (71.1% compared to 78.7%) than RPP members who are not also observed contributing into RRSPs.
6.1 Graphical inspection
Figure 2 shows the first- and second-stage effects of integration on private savings outcomes. Specifically, the plots show average RPP and RRSP contributions as functions of employment income relative to the contribution threshold set by the CPP or QPP. For example, the zero-earnings threshold coincides exactly with income equal to the Year’s Maximum Pensionable Earnings (YMPE) in the reference year. The relative income is grouped into $400 bins over a $12,000 interval for the purpose of generating the graphs; each point corresponds to the average contribution level within that income bin. Throughout, RPP employer contributions are defined as the difference between the pension adjustment (PA) and the employee’s share of contributions (recorded separately in the Longitudinal Administrative Databank [LAD]).
The first-stage results show that RPP employer contributions increase beyond the pensionable earnings threshold, consistent with integration. It is not clear, a priori, whether employee contributions also belong in the first stage—to reflect an effect of integration—or in the second stage—to reflect a personal savings response to the change in employer contributions. If employee contributions are mandatorily integrated, as Frenken (1996) suggests may sometimes be the case, then this variable belongs in the first stage. Yet employees also have some control over their RPP contributions in addition to the rates set out in their plan contracts. However, although some plans permit employees to make additional voluntary contributions above their normal amounts, there is typically no equivalent for reductions. This situation is problematic because the second-stage prediction is that personal savings should fall beyond the earnings threshold, which suggests that employee contributions should be added to the first stage. It turns out that the choice of where to put this variable does not matter; as Figure 2 shows, employee contributions do not change by very much at the CPP or QPP threshold. Whether this implies no behavioural response or simply that plan contracts do not easily facilitate an adjustment along this margin is not clear, as the fraction of RPPs that allow members to make additional contributions is not known.
The second-stage result, in the chart for RRSP contributions for RPP members, shows there is also a large RRSP adjustment in response to the exogenous change in workplace savings. This result implies a reasonable degree of substitution between the two plans, at approximately $0.50 per $1.00.
While the empirical strategy assumes that the integration feature of workplace pensions has an exogenous impact on RPP contributions, which in turn affect RRSP savings, it is important to note that there may also be a direct effect on private savings that is not controlled for in this setup. The fact that the CPP or QPP only provides adequate income replacement in retirement up to the YMPE may induce savers to amass larger private savings on earnings above this threshold.
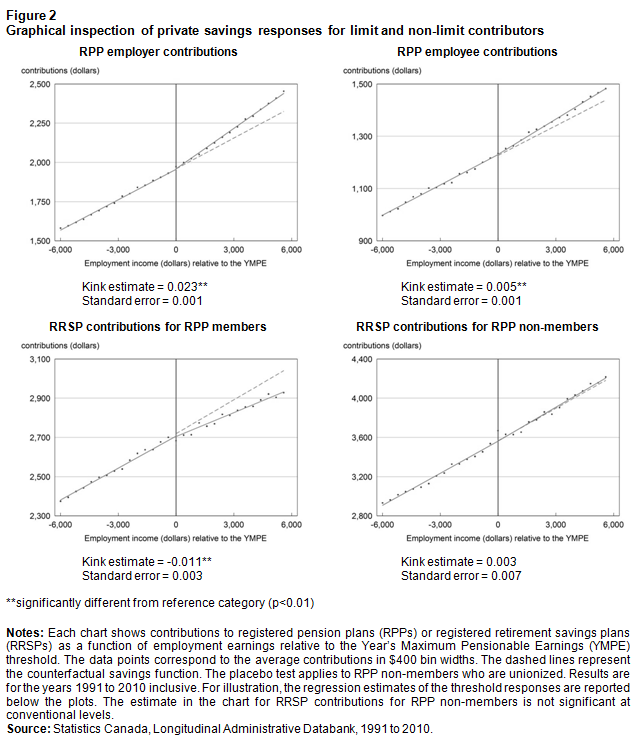
Description for figure 2
The title of the figure is “Graphical inspection of private savings responses for limit and non-limit contributors”
This figure contains four charts which are described below. The four charts represent employment income relative to the Year’s Maximum Pensionable Earnings (YMPE) in the case of registered pension plan (RPP) employer contributions, RPP employee contributions, registered retirement savings plan (RRSP) contributions for RPP members and RRSP contributions for RPP non-members.
Chart title: RPP employer contributions
This is a combined scatter plot and line chart.
The vertical axis (y-axis) is “contributions (dollars),” beginning at 1,500 and ending at 2,500.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at
-6,000 and ending at 6,000.
This chart plots scatter-values of average RPP employer contributions relative to the YMPE threshold. The graph is restricted to individuals earning within $6,000 on either side of the threshold. The graph shows that average contributions are an increasing, linear function of relative earnings, and that there is a discernible upward-kink in the function at the zero-earnings threshold. The graph has a kink estimate of 0.023 that is significant at the 1% level. The standard error is 0.001.
Chart title: RPP employee contributions
This is a combined scatter plot and line chart.
The vertical axis (y-axis) is “contributions (dollars),” beginning at 900 and ending at 1,500.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at
-6,000 and ending at 6,000.
This chart plots scatter-values of average RPP employee contributions relative to the YMPE threshold. In this case, only a trivial increase in the slope is observable. The graph has a kink estimate of 0.005 that is significant at the 1% level. The standard error is 0.001.
Chart title: RRSP contributions for RPP members
This is a combined scatter plot and line chart.
The vertical axis (y-axis) is “contributions (dollars),” beginning at 2,300 and ending at 3,100.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at
-6,000 and ending at 6,000.
This chart plots scatter-values of average RRSP contributions for RPP members relative to the (YMPE) threshold. In this case, a discernible downward-kink in the function at the zero-earnings threshold is seen, consistent with a crowding-out effect. The graph has a kink estimate of 0.011 that is significant at the 1% level. The standard error is 0.003.
Chart title: RRSP contributions for RPP non-members
This is a combined scatter plot and line chart.
The vertical axis (y-axis) is “contributions (dollars),” beginning at 2,800 and ending at 4,400.
The horizontal axis (x-axis) is “Employment income (dollars) relative to the YMPE,” beginning at
-6,000 and ending at 6,000.
This chart plots scatter-values of average RRSP contributions for RPP non-members relative to the YMPE threshold. In this case, no change in the slope is observable. The graph has a kink estimate of 0.003. The standard error is 0.007.
Each chart also reports the ordinary least squares regression estimates of the kink in savings. The reader may refer to Table 5 for these estimates, along with the savings function slope estimates and other relevant information.
Estimates of , from Equation (2), would simultaneously capture an effect of integration and a direct response to the public pension, so would be upward-biased. Workers may also respond directly to the CPP or QPP if they inadvertently view payments into the plan as direct savings. These concerns are addressed by performing a placebo test of the extent to which RRSP contributions respond at the threshold for workers who are unionized but who do not belong to employer-sponsored pensions, shown in the chart for RRSP contributions for RPP non-members. These workers are not affected by integration, so any change in RRSP savings around the YMPE threshold can only result from the CPP or QPP contribution or benefit changes.
Overall, the RRSP savings function for these workers does not appear to respond at all to the pensionable earnings limit. This result suggests the RRSP crowd-out response for RPP members is purely driven by the effect of interest. The fact that a direct response was not observed may arise because CPP or QPP benefits in retirement are determined from a complex formula based on individuals’ lifetime earnings histories and a variety of other personal characteristics. In a given year, marginal deviations in earnings around the YMPE are not expected to influence CPP or QPP benefit entitlements significantly enough to induce behavioural responses in private savings.
6.2 Regression results
Table 4 shows the regression results that correspond to the graphical analysis of the previous subsection. Additional covariates from the LAD that are included in these regressions are: gender; marital status; indicators for age, year, province of residence, employment insurance receipt, union status, and self-employment; as well as information on allowances for disability and medical expenses. Controlling linearly for these covariates removes the influence of other factors affecting savings behaviour from the estimated treatment effect. Note that the analysis only includes individuals who received employment income within $6,000 on either side of the YMPE threshold in the reference year, to reflect the fact that the Regression Kink Design (RKD) estimates a local average treatment effect around the kink. The effects of varying this bandwidth size are tested as a robustness check, below.
| Earnings | Kink | |||
|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | |
| coefficient | standard error | coefficient | standard error | |
| RPP contributions | ||||
| Employer | 0.069Note ** | 0.001 | 0.023Note ** | 0.001 |
| Employee | 0.042Note ** | 0.001 | 0.005Note ** | 0.001 |
| Total | 0.111Note ** | 0.001 | 0.027Note ** | 0.002 |
| RRSP contributions | ||||
| Employee | 0.056Note ** | 0.002 | -0.011Note ** | 0.003 |
| Crowd-out | Note ...: not applicable | Note ...: not applicable | 0.400Note ** | 0.105 |
... not applicable
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||
The results show, first, that the marginal savings rate into RPPs increases by 2.7 percentage points beyond the earnings threshold, from a rate of 11.1% up to 13.8%. This result translates into a significant 24.3% average increase. The magnitude of the response is consistent with expectations from anecdotal descriptions of integration. For comparison, the average employer contribution to the CPP or QPP was 3.2% of earnings over the period of 1991 to 2010. Given that approximately 85% of RPPs use the integration feature, this result suggests that a $1.00 increase in the CPP or QPP contribution leads to a reduction of RPP contributions in the amount . It is important to note, however, that this result applies to an average effect of integration over a 20-year period. It does not imply that a policy reform to the CPP or QPP contribution rate would induce an equally sensitive response, especially in the short run, because RPP contracts tend to be inflexible long-term arrangements.
Second, the table shows that the marginal savings rate into RRSPs decreases beyond the threshold by 1.1 percentage points (or 19.6%). This result is consistent with the rational expectation that these plans are relatively substitutable. However, these findings raise the question of whether substitution derives from an underlying behavioural response or simply from a mechanical effect of the combined RRSP and PA tax-deduction limit for limit contributors. To address this concern, Table 5 separates the results into groups based on whether or not savers are observed contributing strictly below the lesser of their annual tax-deduction limits and the contribution limits specified by the Canada Revenue Agency (CRA). While combined RRSP and PA contributions are permitted to exceed the CRA contribution limits after adjusting for unused room from prior years, using the lesser of the two helps to control for the possibility that savers may be inadvertently responding to the lower limit. The table shows that the first-stage effect of integration is large and significant for both groups, but that the magnitude of crowd-out is larger for limit contributors. The 95% confidence interval of the crowd-out response in Panel A includes unity, because tax regulations prohibit excess contributions and explicitly penalize non-compliance.
| Earnings | Kink | |||
|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | |
| coefficient | standard error | coefficient | standard error | |
| Panel A: Limit contributors | ||||
| RPP contributions | ||||
| Employer | 0.071Note ** | 0.002 | 0.020Note ** | 0.003 |
| Employee | 0.040Note ** | 0.002 | 0.010Note ** | 0.003 |
| Total | 0.112Note ** | 0.002 | 0.031Note ** | 0.004 |
| RRSP contributions | ||||
| Employee | 0.075Note ** | 0.007 | -0.054Note ** | 0.013 |
| Crowd-out | Note ...: not applicable | Note ...: not applicable | 1.736Note ** | 0.388 |
| Panel B: Non-limit contributors | ||||
| RPP contributions | ||||
| Employer | 0.068Note ** | 0.001 | 0.022Note ** | 0.001 |
| Employee | 0.042Note ** | 0.001 | 0.003Note * | 0.001 |
| Total | 0.110Note ** | 0.001 | 0.025Note ** | 0.002 |
| RRSP contributions | ||||
| Employee | 0.045Note ** | 0.001 | -0.014Note ** | 0.003 |
| Crowd-out | Note ...: not applicable | Note ...: not applicable | 0.550Note ** | 0.103 |
... not applicable
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||
Panel B shows that the response is noticeably smaller for non-limit contributors. Nevertheless, RRSP savings still tend to decrease by $0.55 per $1.00 increase in RPPs. This finding implies there is some degree of behavioural substitution between the two plans but that there may also be a role for employer-assisted saving. That is, some of the automatic savings rate change (the remaining $0.45 per $1.00) is still found to pass through into greater wealth accumulation, which may matter for eventual retirement well-being.
Next, to control for the possibility that RRSP contributions respond directly to the CPP or QPP contribution, Equation (2) is augmented as follows:
where is an indicator of pension coverage. Intuitively, this equation augments the RKD to a difference-in-differences setting. In this setting, the parameter of interest, , captures the savings rate change for RPP members (the treatment group) above and beyond any direct response to the YMPE threshold estimated using RPP non-members (the control group). Here, the control group is restricted to unionized workers, based on the previous result from Figure 1 that this group satisfies the sorting restriction. Because most RPP members are also unionized, the restriction also improves comparability of the two groups. A variant of this model would have the coverage indicator interact with the covariates.
The results for non-limit contributors are given in Table 6. First, the table shows that the savings rate into RRSPs for individuals not covered by workplace pensions is 9.7% of earnings; for RPP members, this rate is 5.2 percentage points less. The table also shows that RPP members save less, on average, into their RRSPs by approximately $464 per year. Most importantly, the regressions corroborate the graphical inspection that RRSP savings do not respond directly to the CPP or QPP contribution, given that the kink estimate for the control group is nearly zero. Although the crowd-out response for the treated group is less precisely estimated, the magnitude of the response is unchanged and it is still significant (at the 10% level).
| RPP total contributions | RRSP contributions | Crowd-out | ||||
|---|---|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |
| coefficient | standard error | coefficient | standard error | coefficient | standard error | |
| Panel A: Excludes covariates × treated variables | ||||||
| Control | ||||||
| Earnings | Note ...: not applicable | Note ...: not applicable | 0.094Note ** | 0.004 | Note ...: not applicable | Note ...: not applicable |
| Kink | Note ...: not applicable | Note ...: not applicable | 0.001 | 0.007 | Note ...: not applicable | Note ...: not applicable |
| Treated | ||||||
| Fixed effects | Note ...: not applicable | Note ...: not applicable | -858.035Note ** | 15.501 | Note ...: not applicable | Note ...: not applicable |
| Earnings | 0.110Note ** | 0.001 | -0.048Note ** | 0.004 | Note ...: not applicable | Note ...: not applicable |
| Kink | 0.025Note ** | 0.002 | -0.014Note † | 0.008 | 0.566Note † | 0.311 |
| Panel B: Includes covariates × treated variables | ||||||
| Control | ||||||
| Earnings | Note ...: not applicable | Note ...: not applicable | 0.097Note ** | 0.004 | Note ...: not applicable | Note ...: not applicable |
| Kink | Note ...: not applicable | Note ...: not applicable | -0.001 | 0.007 | Note ...: not applicable | Note ...: not applicable |
| Treated | ||||||
| Fixed effects | Note ...: not applicable | Note ...: not applicable | -463.762Note ** | 24.540 | Note ...: not applicable | Note ...: not applicable |
| Earnings | 0.110Note ** | 0.001 | -0.052Note ** | 0.004 | Note ...: not applicable | Note ...: not applicable |
| Kink | 0.025Note ** | 0.002 | -0.013Note † | 0.008 | 0.525Note † | 0.309 |
... not applicable
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||||
6.3 Robustness checks
Three robustness checks of the primary findings are performed to determine: (1) how the results change when individual-level fixed effects are controlled for; (2) whether the results are sensitive to bandwidth selection; and (3) whether the results change when higher-order polynomials in earnings are included in the regressions. In the remainder of this paper, only individuals who are saving strictly below their tax-deduction limits are analyzed, both for compactness and because they are the group of primary interest.
6.3.1 Individual-specific fixed effects
Table 7 considers how the results change when individual-specific fixed effects are included in the estimating equation. Lee and Lemieux (2010, p. 337) note that the regression discontinuity design sharply contrasts with traditional panel data settings, where the individual-specific error component is allowed to be correlated with other observables, including treatment. Here, the assignment of treatment—i.e., whether individuals earn below or above the YMPE threshold—is random, so including individual fixed effects is not necessary for identification. However, their inclusion should not change the results.
| Earnings | Kink | |||
|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | |
| coefficient | standard error | coefficient | standard error | |
| RPP contributions | ||||
| Employer | 0.039Note ** | 0.001 | 0.018Note ** | 0.001 |
| Employee | 0.035Note ** | 0.001 | 0.002Note * | 0.001 |
| Total | 0.074Note ** | 0.001 | 0.020Note ** | 0.001 |
| RRSP contributions | ||||
| Employee | 0.029Note ** | 0.002 | -0.008Note ** | 0.003 |
| Crowd-out | Note ...: not applicable | Note ...: not applicable | 0.395Note ** | 0.126 |
... not applicable
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||
Indeed, the results are consistent with the baseline findings. Although the magnitudes of both the first- and second-stage effects are now slightly smaller, they both continue to appear statistically significant. Most importantly, these results continue to show that RPP contributions partially displace other savings, in this case by approximately $0.40 per $1.00.
6.3.2 Bandwidth selection
The primary regressions are constrained to individuals earning within $6,000 on either side of the YMPE threshold, as discussed above. Limiting the bandwidth leads to improved precision of the estimates, but also decreases the size of the sample and, in turn, reduces the strategy’s statistical power. As Landais (n.d., p. 19) notes, the RKD is “quite demanding in terms of bandwidth size compared to a regression discontinuity design.” This situation may arise because the sought-after effects tend to be comparatively small and hard to detect.
In this study, a benefit of using the LAD is that its large sample size permits the statistical model to detect and powerfully estimate small changes in personal savings rates. To investigate how the primary results stand up to changes in bandwidth selection, Chart 2 plots crowd-out estimates of 61 separate regressions of varying bandwidth sizes, from $3,000 to $9,000, in $100 increments. Although the estimates tend to be volatile and statistically insignificant for very narrow bandwidths, this tendency levels out for bandwidths exceeding approximately $4,500, and wider bandwidths only serve to improve accuracy.
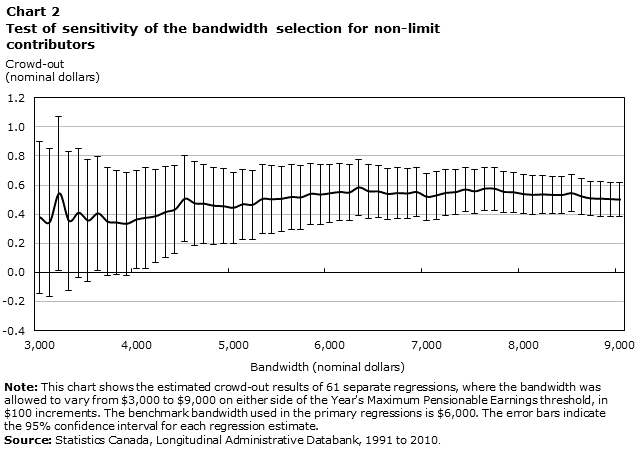
Description for chart 2
The title of the graph is "Chart 2 Test of sensitivity to the bandwidth selection for non-limit contributors."
This is a line chart.
There are in total 61 categories in the horizontal axis. The vertical axis starts at -0.4 and ends at 1.2 with ticks every 0.2 points.
There are 1 series in this graph.
The vertical axis is "Crowd-out
(nominal dollars)."
The horizontal axis is "Bandwidth (nominal dollars)."
The title of series 1 is "Crowd-out."
The minimum value is 0.3335 and it corresponds to "3900."
The maximum value is 0.5841 and it corresponds to "6300."
| Crowd-out (nominal dollars) | |
|---|---|
| 3,000 | 0.3774 |
| 3,100 | 0.3445 |
| 3,200 | 0.5430 |
| 3,300 | 0.3534 |
| 3,400 | 0.4093 |
| 3,500 | 0.3554 |
| 3,600 | 0.4051 |
| 3,700 | 0.3478 |
| 3,800 | 0.3412 |
| 3,900 | 0.3335 |
| 4,000 | 0.3632 |
| 4,100 | 0.3746 |
| 4,200 | 0.3859 |
| 4,300 | 0.4145 |
| 4,400 | 0.4335 |
| 4,500 | 0.5060 |
| 4,600 | 0.4739 |
| 4,700 | 0.4712 |
| 4,800 | 0.4569 |
| 4,900 | 0.4539 |
| 5,000 | 0.4434 |
| 5,100 | 0.4673 |
| 5,200 | 0.4640 |
| 5,300 | 0.5043 |
| 5,400 | 0.5016 |
| 5,500 | 0.5052 |
| 5,600 | 0.5182 |
| 5,700 | 0.5150 |
| 5,800 | 0.5398 |
| 5,900 | 0.5345 |
| 6,000 | 0.5431 |
| 6,100 | 0.5520 |
| 6,200 | 0.5483 |
| 6,300 | 0.5841 |
| 6,400 | 0.5567 |
| 6,500 | 0.5558 |
| 6,600 | 0.5386 |
| 6,700 | 0.5450 |
| 6,800 | 0.5416 |
| 6,900 | 0.5514 |
| 7,000 | 0.5190 |
| 7,100 | 0.5285 |
| 7,200 | 0.5463 |
| 7,300 | 0.5512 |
| 7,400 | 0.5692 |
| 7,500 | 0.5563 |
| 7,600 | 0.5752 |
| 7,700 | 0.5748 |
| 7,800 | 0.5532 |
| 7,900 | 0.5502 |
| 8,000 | 0.5373 |
| 8,100 | 0.5323 |
| 8,200 | 0.5355 |
| 8,300 | 0.5318 |
| 8,400 | 0.5312 |
| 8,500 | 0.5437 |
| 8,600 | 0.5221 |
| 8,700 | 0.5078 |
| 8,800 | 0.5060 |
| 8,900 | 0.5027 |
| 9,000 | 0.4997 |
|
Note: This chart shows the estimated crowd-out results of 61 separate regressions, where the bandwidth was allowed to vary from $3,000 to $9,000 on either side of the Year's Maximum Pensionable Earnings threshold, in $100 increments. The benchmark bandwidth used in the primary regressions is $6,000. The error bars indicate the 95% confidence interval for each regression estimate. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
|
6.3.3 Polynomial order
Table 8 analyzes how the primary results depend on the choice of polynomial order used for the employment income variable. This analysis helps to control for the possibility that the results are inadvertently biased in some way if personal savings is a natural non-linear function of earnings. The results show, first, that the effect of integration on RPP contributions is not dependent on whether a linear, quadratic, or cubic specification is used. In all three cases, contributions are found to increase by approximately 2.2% to 2.5% of earnings beyond the YMPE threshold, which is consistent with the baseline results.
However, the table also shows that the RRSP crowd-out response is close to zero when higher-order polynomials are used. Although the tests of model specification suggest the linear regression should be preferred (see the table’s notes), these findings cast some doubt on the validity of the baseline second-stage results. This concern is addressed in Panel B by repeating the analysis but extending the bandwidth size to $9,000. This extension recognizes the fact that jointly estimating a polynomial function of earnings and a kink may simply be too demanding of the data under the narrower bandwidth. These findings support the baseline result that RRSP contributions respond meaningfully at the YMPE threshold. In addition, all the estimates that appear significant in Panel A do not change when the bandwidth is increased, and the tests of model specification continue to show that the linear regression is preferred.
| RPP total contributions | RRSP contributions | Crowd-out | ||||
|---|---|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |
| coefficient | standard error | coefficient | standard error | coefficient | standard error | |
| Panel A: Bandwidth = $6,000 | ||||||
| Linear | 0.025Note ** | 0.002 | -0.014Note ** | 0.003 | 0.550Note ** | 0.103 |
| Quadratic | 0.022Note ** | 0.006 | -0.001 | 0.009 | 0.045 | 0.427 |
| Cubic | 0.022Note ** | 0.006 | 0.000 | 0.009 | 0.011 | 0.429 |
| Panel B: Bandwidth = $9,000 | ||||||
| Linear | 0.026Note ** | 0.001 | -0.013Note ** | 0.002 | 0.505Note ** | 0.060 |
| Quadratic | 0.021Note ** | 0.004 | -0.013Note * | 0.005 | 0.633Note * | 0.266 |
| Cubic | 0.021Note ** | 0.004 | -0.013Note * | 0.005 | 0.637Note * | 0.263 |
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||||
6.4 Controlling for non-retirement savings
RRSPs are deemed to be a retirement savings vehicle, as the name suggests, but tax regulations do not explicitly restrict the timing of distributions. Although withdrawals are subject to normal income taxes, there is no test of financial hardship or explicit penalty for accessing these funds before the age of retirement. In contrast, RPP contributions lock in usually after a few years of consecutive service or plan membership, and individual retirement accounts (IRAs) in the United States impose a 10% penalty on early withdrawals. Mawani and Paquette (2011) show that RRSPs may be commonly used for precautionary saving and income smoothing in addition to the intended purpose of saving for retirement. Further, the Home Buyers’ Plan (HBP) and the Lifelong Learning Plan are programs that allow individuals to borrow directly from their RRSPs on a penalty-free basis to finance the purchase of a first home or post-secondary education, respectively. RRSP contributions may, therefore, represent the sum of savings for retirement, housing, education, and precautionary purposes. This situation raises the question of whether the substitutability of RPPs and RRSPs differs across workers who are using RRSPs for these different reasons.
The longitudinal component of the data is exploited to address this question. Chart 3 shows how the estimates of crowd-out vary depending on whether or not individuals are: (1) ever observed withdrawing from their RRSPs; and, (2) ever observed defaulting on a repayment due under the HBP. While it is not possible to discern from the data how RRSP contributions are intended to be used, conditioning on future behaviour in this manner gives some insight into how the contributions are actually used. However, the results show that crowd-out is relatively homogeneous across savers who end up using their RRSPs differently.
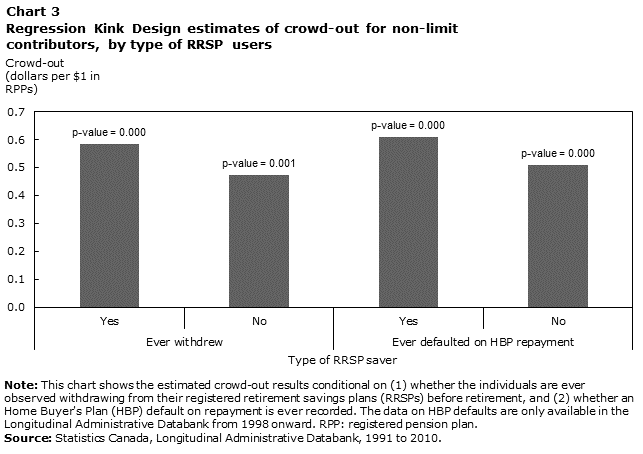
Description for chart 3
The title of the graph is "Chart 3 Regression Kink Design estimates of crowd-out for non-limit contributors, by type of RRSP users
."
This is a column clustered chart.
There are in total 4 categories in the horizontal axis. The vertical axis starts at 0 and ends at 0.7 with ticks every 0.1 points.
There are 1 series in this graph.
The vertical axis is "Crowd-out
(dollars per $1 in RPPs)."
The horizontal axis is "Type of RRSP saver."
The title of series 1 is "Crowd-out."
The minimum value is 0.474 and it corresponds to "Ever withdrew No."
The maximum value is 0.608 and it corresponds to "Ever defaulted on HBP repayment Yes."
| Crowd-out (dollars per $1 in RPPs) | p-values | |
|---|---|---|
| Ever withdrew Yes | 0.585 | 0.000 |
| Ever withdrew No | 0.474 | 0.001 |
| Ever defaulted on HBP repayment Yes | 0.608 | 0.000 |
| Ever defaulted on HBP repayment No | 0.509 | 0.000 |
|
Note: This chart shows the estimated crowd-out results conditional on (1) whether the individuals are ever observed withdrawing from their registered retirement savings plans (RRSPs) before retirement, and (2) whether an Home Buyer's Plan (HBP) default on repayment is ever recorded. The data on HBP defaults are only available in the Longitudinal Administrative Databank from 1998 onward. RPP: registered pension plan. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||
Table 9 extends this analysis along several dimensions. First, the table recognizes that RRSPs do not prevent or discourage early withdrawals. In doing so, it shows how the crowd-out estimate changes using RRSP net contributions (defined as contributions less withdrawals) as the dependent variable in Equation (2), where the sample has been extended to include individuals who are dissaving (Column 1). The results show that controlling for withdrawals does not meaningfully influence the baseline findings. On balance, non-retirement incentives to save in RRSPs do not affect the extent to which these savings respond to exogenous changes in RPP contributions.
The next step is to consider how the results change when taxable savings are controlled for. A limitation of the LAD is that it does not provide direct information on savings in taxable accounts, given that this information is not reported on individuals’ tax forms. Variables for investment income and capital gains are used as proxies for this information. The remaining columns in Table 9 show that there is no discernible effect of a change in RPP contributions on taxable savings. Overall, the baseline results are not sensitive to controlling for this form of saving (Column 2), given that the magnitude of the response of investment income and capital gains at the YMPE threshold is negligible (Column 3). These results do not change if the investment income or capital gains variables are used separately.
| RPP total contributions | Second-stage savings | Crowd-out | ||||
|---|---|---|---|---|---|---|
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |
| coefficient | standard error | coefficient | standard error | coefficient | standard error | |
| RRSP net savings | 0.025Note ** | 0.001 | -0.012Note ** | 0.003 | 0.476Note ** | 0.102 |
| Taxable + RRSP net savings | 0.025Note ** | 0.001 | -0.012Note ** | 0.003 | 0.472Note ** | 0.118 |
| Taxable net savings | 0.025Note ** | 0.001 | 0.000 | 0.001 | 0.004 | 0.047 |
Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||||||
There are several explanations for the lack of taxable savings response. First, as Table 2 showed, average annual investment income and capital gains are relatively small for RPP members, which may render it difficult for individuals to make adjustments along this margin. Second, these plans may be imperfect substitutes because of the lock-in provisions of RPPs, especially if taxable savings are mostly intended for non-retirement purposes. Finally, savers may simply regard RPPs and taxable plans as non-fungible, either because of their differential tax treatment or for other reasons of mental accounting.
6.5 Heterogeneous responses
Although RRSPs have been found on average to substitute partially for RPPs, employer sponsorship may still assist some individuals more than others with the challenging task of preparing for retirement. This issue is addressed by testing for heterogeneous crowd-out responses along several dimensions that are expected to matter for long-term saving.
Chart 4 investigates how crowd-out differs by age group. The findings show that the extent to which an exogenous change in RPP contributions passes through into higher total savings is largest for younger workers, aged 25 to 34, at approximately $0.60 per $1.00 (notwithstanding older workers, aged 55 and over, although a retirement selection effect may also affect this result). These findings may suggest that employer sponsorship plays a greater role for younger households in helping them to save more for retirement sooner in life. In contrast, the larger crowd-out response for individuals aged 45 to 54 is not surprising because the two plans may become more fungible closer to retirement, given that RPP contributions would not be locked in for as long. The fact that crowd-out tends to increase in age may also imply a gradual learning effect.
Next, how the results vary across individuals according to their tax-deduction limits is investigated. As discussed above, individuals’ RRSP and PA deduction limits are determined by the lesser of 18% of income and a regulated maximum ($22,000 in 2010), but unused room also carries forward indefinitely since 1991. Controlling for age, income, and other characteristics, this means individuals’ limits may be interpreted to some extent as a ‘snapshot’ of their previous histories of saving in tax-deductible accounts relative to their previous earnings. Chart 5 shows how the first-stage RPP kink estimate, as well as the resulting crowd-out effect, varies by conditioning on progressively larger unused RRSP contribution room. The results show, first, that the integration effect on RPP contributions is robust in terms of economic relevance and statistical significance (at the 1% level for every regression). However, the second-stage response tends toward zero as the analysis is progressively conditional on larger unused RRSP room. RPP contributions appear to raise total savings more for individuals with evidence of weaker histories of saving in tax-deductible plans. This finding may imply, not surprisingly, that workplace accounts matter more for individuals who would otherwise not be planning as much for their retirement.
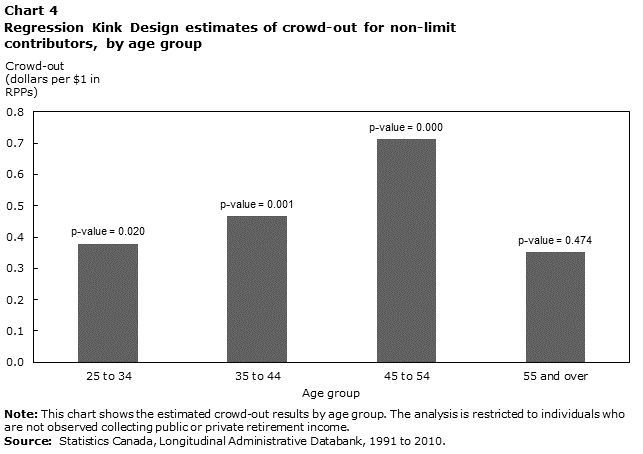
Description for chart 4
The title of the graph is "Chart 4 Regression Kink Design estimates of crowd-out for non-limit contributors, by age group."
This is a column clustered chart.
There are in total 4 categories in the horizontal axis. The vertical axis starts at 0 and ends at 0.8 with ticks every 0.1 points.
There are 1 series in this graph.
The vertical axis is "Crowd-out
(dollars per $1 in RPPs)."
The horizontal axis is "Age group."
The title of series 1 is "Crowd-out."
The minimum value is 0.352 and it corresponds to "55 and over."
The maximum value is 0.712 and it corresponds to "45 to 54."
| Crowd-out (dollars per $1 in RPPs) | p-values | |
|---|---|---|
| 25 to 34 | 0.379 | 0.020 |
| 35 to 44 | 0.466 | 0.001 |
| 45 to 54 | 0.712 | 0.000 |
| 55 and over | 0.352 | 0.474 |
|
Note: This chart shows the estimated crowd-out results by age group. The analysis is restricted to individuals who are not observed collecting public or private retirement income. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||
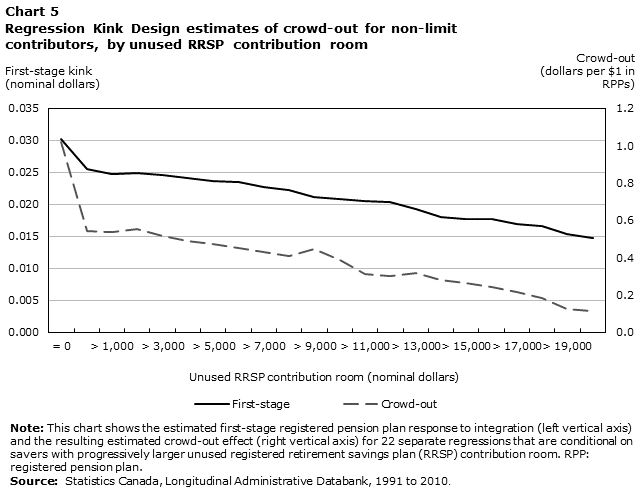
Description for chart 5
The title of the graph is "Chart 5 Regression Kink Design estimates of crowd-out for non-limit contributors, by unused RRSP contribution room."
This is a line chart.
There are in total 22 categories in the horizontal axis. The primary vertical axis starts at 0 and ends at 0.035 with ticks every 0.005 points. The secondary vertical axis starts at 0 and ends at 1.2 with ticks every 0.2 points.
There are 2 series in this graph.
The horizontal axis is "Unused RRSP contribution room (nominal dollars)."
The title of series 1 is "First-stage."
The vertical axis is "First-stage kink
(nominal dollars)."
The minimum value is 0.0147 and it corresponds to "> 20,000."
The maximum value is 0.0303 and it corresponds to "= 0."
The title of series 2 is "Crowd-out."
The vertical axis is "Crowd-out
(dollars per $1 in RPPs)."
The minimum value is 0.1139 and it corresponds to "> 20,000."
The maximum value is 1.0205 and it corresponds to "= 0."
| First-stage | Crowd-out | |
|---|---|---|
| First-stage kink (nominal dollars) | Crowd-out (dollars per $1 in RPPs) | |
| = 0 | 0.0303 | 1.0205 |
| > 0 | 0.0255 | 0.5431 |
| > 1,000 | 0.0247 | 0.5355 |
| > 2,000 | 0.0249 | 0.5538 |
| > 3,000 | 0.0246 | 0.5144 |
| > 4,000 | 0.0241 | 0.4905 |
| > 5,000 | 0.0237 | 0.4731 |
| > 6,000 | 0.0235 | 0.4515 |
| > 7,000 | 0.0227 | 0.4277 |
| > 8,000 | 0.0223 | 0.4089 |
| > 9,000 | 0.0211 | 0.4487 |
| > 10,000 | 0.0209 | 0.3878 |
| > 11,000 | 0.0206 | 0.3115 |
| > 12,000 | 0.0203 | 0.2991 |
| > 13,000 | 0.0192 | 0.3163 |
| > 14,000 | 0.0180 | 0.2779 |
| > 15,000 | 0.0177 | 0.2657 |
| > 16,000 | 0.0177 | 0.2414 |
| > 17,000 | 0.0169 | 0.2179 |
| > 18,000 | 0.0166 | 0.1818 |
| > 19,000 | 0.0154 | 0.1251 |
| > 20,000 | 0.0147 | 0.1139 |
|
Note: This chart shows the estimated first-stage registered pension plan response to integration (left vertical axis) and the resulting estimated crowd-out effect (right vertical axis) for 22 separate regressions that are conditional on savers with progressively larger unused registered retirement savings plan (RRSP) contribution room. RPP: registered pension plan. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||
Chart 6 corroborates this finding by presenting data for individuals conditional on different observed histories of saving in RRSPs. The results show that crowd-out is only detected for individuals who have prior experience using such plans. This outcome may arise either because of a gradual learning effect or because individuals who save the least also tend to respond the least rationally to exogenous changes in savings. Altogether, the findings could be interpreted as suggesting employer sponsorship and other forms of automatic saving matter a great deal in helping more vulnerable groups save for their retirement.
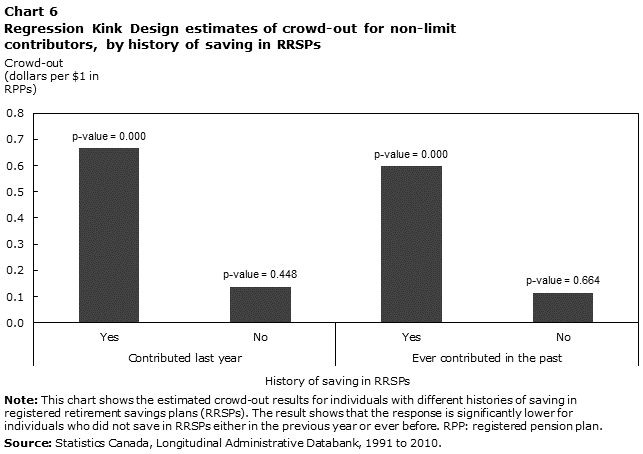
Description for chart 6
The title of the graph is "Chart 6 Regression Kink Design estimates of crowd-out for non-limit contributors, by history of saving in RRSPs
."
This is a column clustered chart.
There are in total 4 categories in the horizontal axis. The vertical axis starts at 0 and ends at 0.8 with ticks every 0.1 points.
There are 1 series in this graph.
The vertical axis is "Crowd-out
(dollars per $1 in RPPs)."
The horizontal axis is "History of saving in RRSPs."
The title of series 1 is "Crowd-out."
The minimum value is 0.115 and it corresponds to "Ever contributed in the past No."
The maximum value is 0.667 and it corresponds to "Contributed last year Yes."
| Crowd-out (dollars per $1 in RPPs) | p-values | |
|---|---|---|
| Contributed last year Yes | 0.667 | 0.000 |
| Contributed last year No | 0.138 | 0.448 |
| Ever contributed in the past Yes | 0.598 | 0.000 |
| Ever contributed in the past No | 0.115 | 0.664 |
|
Note: This chart shows the estimated crowd-out results for individuals with different histories of saving in registered retirement savings plans (RRSPs). The result shows that the response is significantly lower for individuals who did not save in RRSPs either in the previous year or ever before. RPP: registered pension plan. Source: Statistics Canada, Longitudinal Administrative Databank, 1991 to 2010. |
||
7 Conclusion
This paper provided new evidence on the effect of workplace pensions on other private savings. While this issue has drawn a lot of research attention in the past, mostly concerning the growth of 401(k)s in the United States, the debate remains unresolved largely due to limitations in the data and suitable research designs (Bernheim 2002). These concerns were addressed by exploiting a unique feature of workplace pensions in Canada to causally identify their effect on other savings behaviour. Specifically, most plans have integrated contribution formulas with the contribution schedule of the Canada Pension Plan (CPP) or Québec Pension Plan (QPP), so individuals’ marginal savings rates into registered pension plans (RPPs) tend to increase exogenously when their earnings surpass a pre-specified threshold. The Regression Kink Design was used to jointly estimate the effect of integration on workplace pension contributions and the resulting displacement effect on other savings.
The results showed that, first, CPP or QPP contributions affect employers’ generosity with regard to RPP contributions on a dollar-for-dollar basis. It is important to note, however, that this finding corresponds to a locally estimated response spanning a 20-year time period; changes in the CPP or QPP contribution rate may not induce an equally sensitive response, especially in the short run. Nevertheless, the extent to which the integration feature of RPPs has been found to influence private savings may inform discourse about the future direction of the CPP or QPP. Second, the results showed that, on balance, RPP contributions partially displace savings in registered retirement savings plans (RRSPs), although no similar effect was found for taxable savings as reflected by investment income and capital gains. For workers saving strictly less than their contribution limits, RRSP contributions decrease by approximately $0.50 per $1.00 increase in RPP savings. This finding is perhaps consistent with rational expectations, but may also imply a role for employer-assisted saving given that the estimates show a large fraction still passes through into greater wealth accumulation. The response was also found to be much smaller for workers with weaker histories of saving in retirement accounts. This finding is consistent with previous research showing that automatic savings matter a great deal in helping more vulnerable groups save for their retirement (Chetty et al. 2014).
However, several noteworthy issues remain unresolved. First, although this paper detected a crowd-out response for workers earning close to the average industrial wage, the extent to which these results can be generalized to the full population of tax filers is not clear. Second, as mentioned above, only approximately half of RPP members are also observed saving in RRSPs. While it is unknown whether the other half are also responding along other unobserved margins (e.g., home equity accumulation, consumption of durable goods), the automatic savings rate change may significantly improve the savings outcomes of a large group of workers. Finally, it is unclear whether the heterogeneous responses derive from underlying differences in workers’ rational preferences for saving or from some other reason altogether. A growing body of research in behavioural economics finds that many workers know very little about the details of their pension plans (Mitchell 1988; Luchak and Gunderson 2000), they behave myopically (Laibson 1997), and they are easily influenced by simple design features of their plans (Madrian and Shea 2001; Choi et al. 2004). The extent to which savings programs affect individuals differently based on their cognitive abilities to recognize, understand, and respond to such programs is a promising direction for future research.
References
Alessie, R.J.M., A. Kapteyn, and F. Klijn. 1997. “Mandatory pensions and personal savings in the Netherlands.” De Economist 145 (3): 291–324.
Baker, M., J. Gruber, and K. Milligan. 2007. “Simulating the response to reform of Canada.” In Social Security Programs and Retirement around the World: Fiscal Implications of Reform, ed. J. Gruber and D.A. Wise, p. 83–118. Chicago: University of Chicago Press.
Baldwin, B. 2007. Registered Pension Plans in Canada – Their evolution, structure and challenges. Prepared for the Human Resources and Skills Development Canada Strategic Analysis, Audit and Evaluation Branch. Ottawa: HRSDC.
Benjamin, D.J. 2003. “Does 401(k) eligibility increase saving? Evidence from propensity score subclassification.” Journal of Public Economics 87 (56): 1259–1290.
Bernheim, B.D. 2002. “Taxation and saving.” In Handbook of Public Economics, ed. A.J. Auerbach and M. Feldstein, p. 1173–1249. Elsevier.
Chetty, R., J.N. Friedman, S. Leth-Petersen, T. Nielsen, and T. Olsen. 2014. “Active vs. passive decisions and crowdout in retirement savings accounts: Evidence from Denmark.” Quarterly Journal of Economics 129 (3): 1141–1219.
Choi, J.J., D. Laibson, B.C. Madrian, and A. Mertick. 2004. “For better or for worse: Default effects and 401(k) savings behavior.” In Perspectives on the Economics of Aging, ed. D.A. Wise. Chicago: University of Chicago Press.
Engelhardt, G.V., and A. Kumar. 2011. “Pensions and household wealth accumulation.” Journal of Human Resources 46 (1): 203–236.
Engen, E.M., W.G. Gale, and J.K. Scholz. 1994. “Do saving incentives work?” Brookings Papers on Economic Activity 1994 (1): 85–180.
Engen, E.M., W.G. Gale, and K. Scholz. 1996. “The illusory effects of saving incentives on saving.” Journal of Economic Perspectives 10 (4): 113–138.
Euwals, R. 2000. “Do mandatory pensions decrease household savings? Evidence from the Netherlands.” De Economist 148 (5): 643–670.
Frenken, H. 1995. “RRSPs – unused opportunities.” Perspectives 1995 (Winter). Statistics Canada Catalogue no. 75-001-X.
Frenken, H. 1996. “The impact of changes in the Canada Pension Plan on private pensions.” Canadian Business Economics 1996 (Summer): 65–72.
Gale, W.G. 1998. “The effects of pensions on household wealth: A reevaluation of theory and evidence.” Journal of Political Economy 106 (4): 706–723.
Gelber, A.M. 2011. “How do 401(k)s affect saving? Evidence from changes in 401(k) eligibility.” American Economic Journal: Economic Policy 3 (4): 103–122.
Hubbard, R.G., and J.S. Skinner. 1996. “Assessing the effectiveness of saving incentives.” Journal of Economic Perspectives 10 (4): 73–90.
Ippolito, R.A. 1997. Pension plans and employee performance. Chicago: University of Chicago Press.
Iwry, M.J., and D.C. John. 2009. Pursuing universal retirement security through automatic IRAs. The Retirement Security Project, no. 2009-03. Washington, D.C.: The Brookings Institution.
Laibson, D. 1997. “Golden eggs and hyperbolic discounting.” The Quarterly Journal of Economics 112 (2): 443–478.
Landais, C. n.d. “Assessing the welfare effects of unemployment benefits using the regression kink design.” American Economic Journal: Economic Policy. Forthcoming.
Lee, D.S., and T. Lemieux. 2010. “Regression discontinuity designs in economics.” Journal of Economic Literature 48 (June): 281–335.
Luchak, A.A., and M. Gunderson. 2000. “What do employees know about their pension plan?” Industrial Relations: A Journal of Economy and Society 39 (4): 646–670.
Madrian, B.C., and D.F. Shea. 2001. “The power of suggestion: Inertia in 401(k) participation and savings behavior.” Quarterly Journal of Economics 116 (4): 1149–1187.
Mawani, A., and S. Paquette. 2011. “Pre-retirement RRSP withdrawals.” Canadian Tax Journal 59 (2): 183–219.
Milligan, K. 2002. “Tax-preferred savings accounts and marginal tax rates: Evidence on RRSP participation.” Canadian Journal of Economics 35 (3): 436–456.
Mitchell, O.S. 1988. “Worker knowledge of pension provisions.” Journal of Labor Economics 6 (1): 21–39.
Morissette, R., and Y. Ostrovsky. 2006. Pension coverage and retirement savings of Canadian families, 1986 to 2003. Analytical Studies Branch Research Paper Series, no. 286. Statistics Canada Catalogue no. 11F0019M.
Ostrovsky, Y., and G. Schellenberg. 2009. Pension coverage, retirement status, and earnings replacement rates among a cohort of Canadian seniors. Analytical Studies Branch Research Paper Series, no. 321. Statistics Canada Catalogue no. 11F0019M.
Poterba, J.M., S.F. Venti, and D.A. Wise. 1994. “401(k) plans and tax-deferred saving.” In Studies in the Economics of Aging, ed. D.A. Wise, p. 105–142. Chicago: University of Chicago Press.
Poterba, J.M., S.F. Venti, and D.A. Wise. 1995. “Do 401(k) contributions crowd out other personal saving?” Journal of Public Economics 58 (1): 1–32.
Statistics Canada. 1996. Canada’s retirement income programs: A statistical overview. Statistics Canada Catalogue no. 74-507-X.
Statistics Canada. 2003. Canada’s retirement income programs: A statistical overview (1990-2000). Statistics Canada Catalogue no. 74-507-X.
Thaler, R.H., and S. Benartzi. 2004. “Save More TomorrowTM: Using behavioral economics to increase employee saving.” Journal of Political Economy 112 (S1): S164–S187.
Thaler, R.H., and C.R. Sunstein 2008. Nudge: Improving decisions about health, wealth, and happiness. New Haven, Connecticut: Yale University Press.
Veall, M.R. 2001. “Did tax flattening affect RRSP contributions?” Canadian Journal of Economics 34 (1): 120–131.
Venti, S.F., and D.A. Wise. 1996. The wealth of cohorts: Retirement saving and the changing assets of older Americans. Working Paper 5609. Cambridge, Massachusetts: National Bureau of Economic Research.
- Date modified: