Using the census to research your family history—Part 2: tips and best practices
In our last post, we looked at how the census works and what kind of information you can find in it. Now we will discuss tips and best practices for using the census to research your family history.
Where to find the census
Canadian censuses are transferred to Library and Archives Canada (LAC) 92 years after they are conducted. Those from 1825 to 1926 are available for research in online databases. By selecting a database, you can access more information about a particular census, as well as the link to the database itself. Only one census can be researched at a time.
LAC also holds census records that have not all been digitized or put into a database, including those from 1640 to 1825. Records in microfilm format from Newfoundland and Labrador are available for the years 1921, 1935 and 1945. Visit LAC's Finding Aid 300 page to learn more about the information available from these time periods and how to access it.
There are other websites that allow you to research Canadian censuses—in some cases, multiple censuses at once—though many require a paid subscription. These databases include the following:
- Ancestry
- 1825, 1842 to 1921
- subscription required, free at many public libraries
- available in English and French
- Automated Genealogy
- 1851, 1901, 1906, 1911 and some of 1921 in New Brunswick
- free
- available in English only
- FamilySearch
- 1825 to 1926; Manitoba, 1831 to 1870; and Newfoundland 1921, 1935 and 1945
- free
- available in English and French
- FindMyPast
- 1825, 1842 to 1911
- subscription required
- available in English only
- Programme de recherche en démographie historique (PRDH)
- 1666, 1667, 1681, 1688, 1700, 1716 and 1744
- subscription and free versions available
- available in English and French.
Starting your family history research
To get started, all you need is some information. Ask relatives about the names of your ancestors, where they lived, their dates of birth and anything else you can uncover. Listen to family stories and write down everything you learn. Now you can start doing some research.
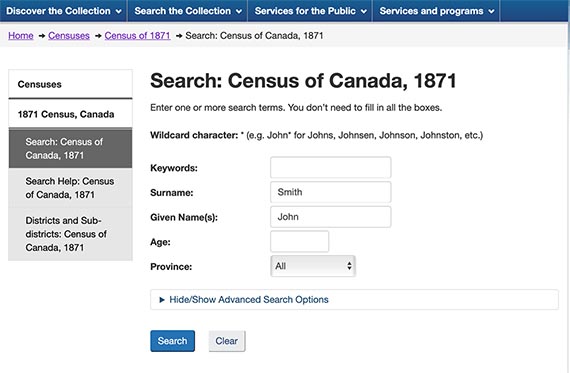
Each website has its own search engine. Since most Canadian census documents come from Library and Archives Canada (LAC), we will focus on its search engine. Using the information you have gathered, choose the census you think will be most relevant. For example, if your ancestor was born in 1869, the 1871 Census would be the first to list a record of them.
Most databases allow you to search by name, place and location. Many also have the option to search by keyword, so you can look for just about anything. Then, all you need to do is use "Enter."
Once you have entered your search terms, you will see a list of results that contains additional basic information. For example, if you're looking for a John Smith in Sherbrooke who was born around 1823, the first entry below looks promising.
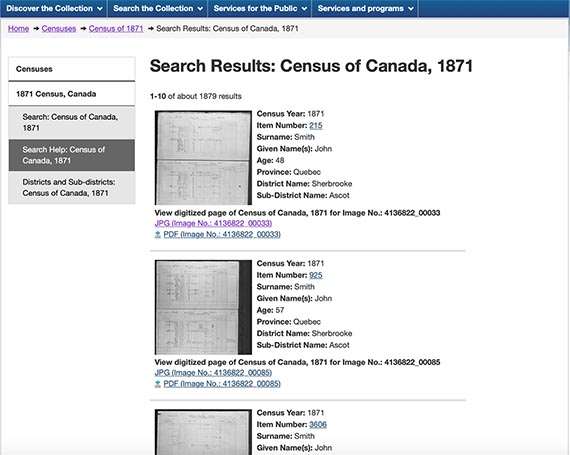
Choose to view the actual manuscript census as either a JPG or a PDF and then browse the list of names to find the one you're looking for. You can select the item number to see the full reference, including birthplace and religion.
Best practices to keep in mind
In an ideal situation, you would simply enter a name into a census database and be rewarded with the information you're looking for. But in many cases, research is a little more complicated. Sometimes you'll have trouble finding the information you want, and other times you'll see so many entries that it will be difficult to find the right one. Here are some suggestions to make your research go smoothly.
Check names
When it comes to using the census to research your family history, it is important to avoid searching only by name. Names provided on the census can be deceptive for a number of reasons. Sometimes names are repeated from generation to generation or they are very common. Sometimes there are errors in the database because the indexer could not read the enumerator's handwriting. The spelling of a name can also change over time.
Cross-reference
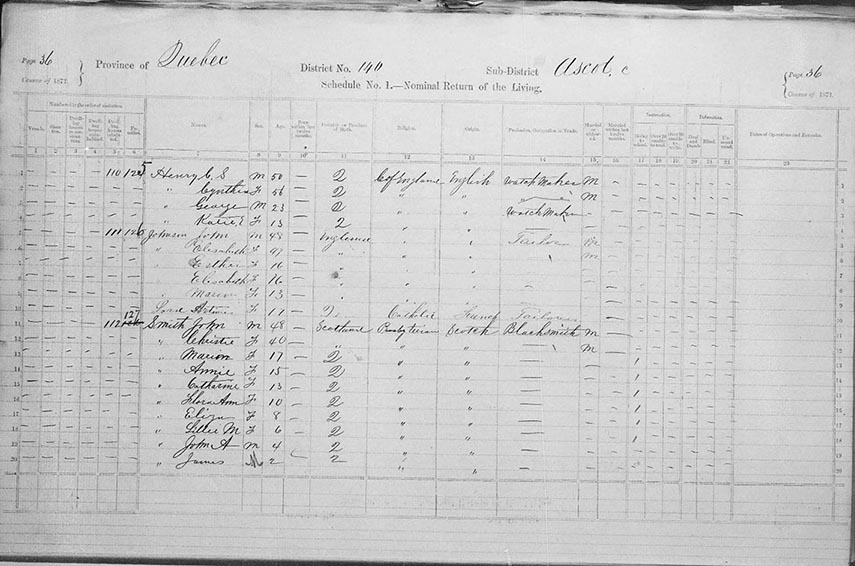
Whenever you can, it's always a good idea to cross-reference any information you find. Sometimes this means going back and forth to trace your family through multiple censuses. You can cross-reference information with birth, marriage and death certificates; city directories; immigration records; military records; and more. For example, you can imagine that there may have been more than one John Smith born in 1823 in Sherbrooke. So how do you know if you have found the right one?
Now let's say you have found your relative John Smith's marriage certificate declaring he wed a woman named Christie. After you have downloaded the image, you can zoom in and see that the census record for this John Smith shows that he is married to a woman named Christie and that together they have nine children. You know that John Smith and Christie Smith are married because it is marked in column 15. So there is a good chance you found a match. If not, you can go back to the search results and try another option.
Be creative
Research can be more of an art than a science and, in many cases, it can be helpful to take a creative approach. For example, you can try tracking your ancestor through multiple censuses to ensure you have the right person. This can mean going backward and forward in time. In other cases, you can try using several different search terms in combination. You can also find information by looking at the neighbourhood a person lived in, the kind of work they did and even how their lives changed over the years.
Don't give up!
Researching your family history can be challenging, but that's alright. This work is more of a marathon than a sprint, and it will take time. At the same time, new censuses are being released every few years, and databases are constantly being updated with new information as well as corrections. So be sure to keep checking back. If you run into problems, you can always ask for help. There's an amazing community of family historians and genealogists around the world.
The census and your family history
We can learn so much about our family history through the census. Do you want to learn how you can use the census to find out more about your family's history? Check out our other blog posts!
- Using the census to research your family history—Part 1: introduction to the census
- Using the census to research your family history—Part 3: concrete example
- The life of an 1871 Census enumerator
If you would like more information on using the census to do research, check out this detailed guide from Library and Archives Canada.