Value-added exports: measurement framework

Ziad Ghanem and Lyming Huang

Industry Accounts Division

July 3, 2014

Skip to text

1. Introduction
2. The Value-added exports database
3. Measurement framework
4. Numerical example
5. Comparison of VAE to the OECD-WTO Trade in Value-added database
References

Text begins

1. Introduction

Globalization has brought about an increase in the gross flows of trade. While an important measure of the interconnectedness of economies, this increase in gross flows cannot be easily related to domestic value-added. To fill this important analytical gap, Statistics Canada is publishing a value-added exports database that provides a set of analytical measures of trade to complement the basic statistics on the gross exports and imports of goods and services.

The value-added exports database shows the exports and imports of industries, as well as the direct and indirect impacts of each industry's production for exports on total value-addedNote 1, jobs, and imports. These estimates provide a measure of the importance of each industry's exports for the entire economy. The database also includes the indirect impacts of all production for exports on each specific industry, thereby providing a measure of an industry's total reliance on exports beyond its own direct exports. Figures are separately articulated for U.S. and non-U.S. exports and imports.

The basic measurement framework relies on modelling methods that quantify the contribution of exports to domestic value-added and employment. These methods are based on tracking imports and domestic inter-industry transactions related to the production of exports. The main data sources are the input-output (IO) tables, which are published by Statistics Canada with a three year lag from their reference period. Geographic detail on U.S. and non-U.S. trade, which is not available from the IO tables, is compiled from merchandise trade and balance of payment statistics. Goods are attributed to the country of origin or destination in accordance with the customs-based merchandise trade statistics and services in accordance with balance of payments statistics. The industry jobs figures are from the Labour Productivity Measures.

The rest of this document is divided as follows. Section 2 provides a description of the database variables. Section 3 explains the basic measurement framework. Section 4 presents numerical examples of some of the basic calculations. Section 5 briefly compares the Canadian value-added exports framework to the Trade in Value-Added (TiVA) database published by the OECD and WTO and finally some basic evidence from the 2010 figures is shown in an annex to help illustrate the discussions.

2. The Value-added exports database

The data are presented according to the input-output industry classification system, which consists of 234 industries at the detailed level. The list and description of the variables in the database are provided in Table 1. Both the export and import figures exclude re-exported imports. Re-exports are products that are imported and that are subject to a change in ownership but that are not subject to any substantial transformations in the domestic economy before being exportedNote 2. Exports from inventory withdrawals are also excluded from the figures to avoid exaggerating the share of exports in each year's total production.

Table 1
List and description of variables
Table summary
This table displays the results of List and description of variables. The information is grouped by Variable (appearing as row headers), Title and Description (appearing as column headers).
Variable Title Description
YEAR Year Figures are currently available for 2007 to 2011
INDUSTRY Industry 233 industries, classified according to the input-output NAICS-based industry classification.
X Exports Domestic exports, excluding re-exports.
VA Value-added Value-added at basic prices by industry.
VADX Direct value-added exports Direct value-added attributable to the industry's exports.
VAX Value-added exports Total value-added attributable to the industry's exports. The sum of direct value-added and the value-added generated in all other upstream industries.
VAXFD Value-added due to foreign demand The impact on an industry's value-added from exports by all industries. Includes direct value-added from the industry's own exports and all indirect value-added from all other industries' exports.
VAXS Services value-added embodied in exports Domestic services value-added embodied in exports
M Imports Imports.
MUSE Imports of intermediate inputs Imports of intermediate inputs.
MX Imports embodied in exports The sum of direct and indirect imports embodied in the production of exports.
L Jobs Total number of jobs.
LDX Direct jobs embodied in exports Direct jobs attributable to the industry's exports.
LX Total jobs embodied in exports Total jobs attributable to the industry's exports. The sum of direct jobs and the jobs generated in all other upstream industries.
LXFD Jobs due to foreign demand The impact on an industry's jobs from exports by all industries. Includes direct jobs from the industry's own exports and all indirect jobs from all other industries' exports.

3. Measurement framework

In general terms, the contribution of exports to domestic value added is based on removing the double counting of all imported intermediate inputs used in the production of exported goods and services. Intermediate inputs are the goods and services, excluding fixed assets, consumed in the production process.

Figure 1 illustrates the basic framework of value-added exports. As shown in this example, value-added exports are equal to the value of gross exports less the value of imported intermediate inputs used in the production of the exported products ($400 = $600 - $200). These imported inputs must account for the consumption of imports in both the industry producing the exports as well as all upstream industries supplying inputs to the exporting industry.

Figure 1 Basic framework of value-added exports

Description for figure 1

Basic framework of value-added exports

This diagram shows Canada exporting $600 to the rest of the world. This is decomposed into $200 in imports of intermediate inputs used in producing exports and a residual of $400, which represents the amount of value-added exports to the rest of the world.

Value-added exports are derived from calculations that are based on the rectangular, industry-by-product IO tablesNote 3. The IO tables show the use of products and primary inputs by industries in the production of supplies to other industries and to final expenditures as well as the type of final expenditures by product. The information contained in the rectangular input-output tables can be rearranged schematically in the supply and use framework shown in Figure 2. The tables are organized as matrices and vectors to illustrate the mathematical framework. Capital letters denote matrices, the small letters vectors, and the attachment of a superscript (T) the transposes of matrices and vectors.

The rectangular input-output tables show the supply of products by domestic producers (V) and from imports (m), value-added components by industry (W), the uses of products by industries (U) domestic final demands (f) and exports (x). Exports are articulated by product but not by supplying industry and similarly, imports are articulated by product but not by purchasing industry. Two basic accounting identities characterize the system: the total supply of each product must equal its total uses and the total output of an industry must equal its total inputs.

Figure 2 Input-output framework

Description for figure 2

Input-output framework

This diagram shows the basic structure of the supply and use tables. The supply table includes industry outputs and imports by product organized into an output matrix (V) of dimensions product by industry and a vector of imports (m) by product. The supply table also includes a vector of total outputs (g) by industry, a vector of total product output (q) and a vector of total supply by product defined as the sum of the output by product and import by product vectors.

The use table includes industry and final uses of products organized into a matrix of the use of intermediate inputs (U) of dimensions product by industry, a matrix of value-added components (W) of dimensions components by industry, a vector of domestic final demand (f) by product, and a vector of exports (x) by product. The use table also includes a vector of total industry output (g) and a vector of total use by product based on the sum of intermediate inputs, domestic final demand and exports by product.

In the input-output modeling frameworkNote 4, industry output is related to the sum of domestic demands for intermediate inputs and final consumption and foreign demand (exports) through the following accounting identityNote 5:

g=D[(I−μˆ)(Bg+f)+x]      (1)

where D is a matrix of industry market shares by product of dimensions industry by product, used to allocate products to their industry of origin

D=V[diag(q)]−1      (2)

B is a matrix of intermediate input coefficients, of dimensions product by industry, used to estimate the intermediate inputs required to produce industry outputs

B=U[diag(g)]−1      (3)

and μˆ is a diagonal matrix of import shares by product, which is defined as the share of imports in total domestic demand; more easily calculated as the share of imports in total supply net of exports, and which is used to calculate import leakages from domestic production

μˆ=diag(m)[diag(q−x+m)]−1      (4)

By isolating g in equation (1), domestic output by industry can be defined as a function of two basic elements, final expenditures and an inverse which embeds all inter-industry transactions required to produce those final expenditures:

g=[I−D(I−μˆ)B]−1D[(I−μˆ)f+x]      (5)

The bracketed inverse, generally referred to as the Leontief or input-output inverse, [I−D(I−μˆ)B]−1, creates a link between final expenditures and all required production activities, inclusive of direct and all indirect (upstream) production activities. Focusing on the exports portion of final expenditures, the contribution of foreign demand to value-added by all industries, VAX, can thus be derived from:

VAX=vˆ[I−D(I−μˆ)B]−1Dx      (6)

where vˆ is a diagonalized vector of value-added to output ratios by industry, of dimensions industry by industry.

A useful term embedded in equation (1) is Dx; the pre-multiplication of the exports vector x by the market share matrix D, provides an estimate of gross exports by industry.

Similarly to equation (6), the contribution of exports to jobs, LX, can be defined as

LX=lˆ[I−D(I−μˆ)B]−1Dx      (7)

where lˆ is a diagonalized vector of jobs to output ratios by industry, of dimensions industry by industry.

The value of imports both directly and indirectly embodied in exports, MX, can be derived from the industry import coefficients and the exports-related outputs of industries:

MX=ρˆ[I−D(I−μˆ)B]−1Dx      (8)

where ρˆ is a diagonalized vector of import shares by industry, derived through the multiplication of the average import shares by product and the input coefficients matrix:

ρˆ=diag(μ′B)      (9)

The Leontief inverse accounts for all upstream impacts on the output of an industry as well as direct impacts. Measures that focus on the direct impacts of exports on value-added, VADX, excluding impacts on upstream, supplying industries, do not require the use of the inverse and can be simply derived from the pre-multiplication of the shares of industry outputs associated with exports (Dx) by the industry value-added to output ratios, as shown in equation (10); and similarly for the direct impact of exports on jobs, LDX, through the industry jobs to output ratios, in equation (11):

VADX=vˆDx      (10)

LDX=lˆDx      (11)

Aside from measuring impacts of all exports on each specific industry, it is also possible to measure the impacts of an industry's exports on the rest of the economy. This information can be derived from information in the rows of the Leontief inverse, as opposed to focusing on information in the columns as was done above. VAXFD, the impact of exports by all industries on an industry's value-added can be derived from:

VAXFD=[vˆ[I−D(I−μˆ)B]−1diag(Dx)]i      (12)

Similarly LXFD, the impact of an industry's exports on jobs in all other industries can be derived from:

LXFD=[lˆ[I−D(I−μˆ)B]−1diag(Dx)]i      (13)

Product imports are converted into industry imports, M, based on the assumption that imported products have the same industry of origin as domestically produced products:

M=Dm      (14)

Imports of intermediate inputs by industry, MUSE, are based on multiplying the intermediate inputs of industries by the average import shares of products:

MUSE=μ′U      (15)

The two main underlying assumptions of the model relate to the homogeneity of production functions and the proportional allocation of supply. The first assumption is that each industry produces all its different outputs using a single production function. The second assumption is that each exported product is produced by industries based on their average market shares among domestic producers; and that all domestic demands are supplied from domestic industries and imports in proportion to their shares in total domestic demand by product.

These simplifying assumptions undermine the precision of the modeled estimates. The industries of origin of exports and of inputs used in their production, including the imported inputs, may differ from what average market shares may indicate; thus undermining the precision of the estimates. Furthermore, the use of a single industry-level production function may not properly reflect the differentiated production functions of domestic and world-market oriented firms, especially in the context of the growing globalization of production. In reality though, this latter assumption may not be as limiting as it may first appear. The high level of detail provided by the Canadian supply-use tables (234 industries by 470 products) likely classifies producing units and their products into highly homogeneous groupings.

4. Numerical example

This section provides a numerical example to illustrate the basic calculations. The first part provides an overview of the supply and use tables; the second part shows the calculations required for estimating the direct impacts of exports; and the third part shows the slightly more involved methods required to derive the total impacts of exports.

The estimates generated in sections 4.2 and 4.3 are only for demonstrative purposes. The high level of aggregation of the data undermines the precision of the calculations. Furthermore, for the sake of simplicity, the demonstration abstracts from the more differentiated treatment of certain elements such as re-exports and the expenditures of Canadian households while abroad.

4.1 Input-output tables

Tables 2 and 3 provide a numerical example of the industry-by-product input-output tables organized into the supply-use frameworkNote 6. The supply table (Table 2) shows the output of products by domestic industries and international imports of products. The last row of the supply table shows total output by industry, total imports and total supply. The last column of the supply table shows total supply by product as the sum of domestically produced and imported products.

The use table (Table 3) shows the use of goods and services by product and by type of use, i.e. as intermediate consumption of industries, final use for consumption, gross capital formation and exports. It also contains the components of value-added by industry, i.e. labour income, gross mixed income, gross operating surplus, and other taxes net of subsidies on production. The last column of the use table shows total uses by product as the sum of domestic uses and international exports.

Table 2
Supply table
Table summary
This table displays the results of Supply table. The information is grouped by Products (appearing as row headers), Industries, Output, Total output, Imports, Total supply, Primary, Construction, Manufacturing and Services, calculated using units units of measure (appearing as column headers).
Products Industries
Output Total output Imports Total supply
Primary Construction Manufacturing Services
units
Agriculture and forestry 62 0 1 0 63 9 73
Mining 170 0 1 0 171 38 209
Utilities 43 0 0 8 52 1 52
Construction 0 260 0 0 260 0 260
Manufacturing 1 0 537 3 541 381 922
Services 10 2 36 1,959 2,008 89 2,098
Taxes net of subsidies on products Cell with no data Cell with no data Cell with no data Cell with no data Cell with no data -3 -3
Total 286 263 576 1,971 3,095 515 3,611
Table 3
Use table at basic prices
Table summary
This table displays the results of Use table at basic prices. The information is grouped by Products (appearing as row headers), Industries, Input, Final uses, Total uses, Primary, Construction, Manufacturing, Services, Final consumption expenditures by households, Final consumption expenditures by NPISH, Final consumption expenditures by government, Gross fixed capital formation, Changes ininventories and Exports, calculated using units units of measure (appearing as column headers).
Products Industries
Input Final uses Total uses
Primary Construction Manufacturing Services Final consumption expenditures by households Final consumption expenditures by NPISH Final consumption expenditures by government Gross fixed capital formation Changes ininventories Exports
units
Agriculture and forestry 14 1 31 2 10 0 0 0 -1 17 73
Mining 17 14 75 5 3 0 0 8 2 85 209
Utilities 3 0 9 15 22 0 0 0 0 2 52
Construction 4 0 1 28 0 0 0 226 0 0 260
Manufacturing 26 72 197 118 181 0 0 65 -1 264 922
Services 51 60 96 687 623 24 366 74 1 115 2098
Taxes net of subsidies on products -3 2 0 4 76 0 0 15 0 0 95
Value added at basic prices 173 113 167 1111 0 0 0 0 0 0 1564
Taxes net of subsidies on production 6 5 2 59 0 0 0 0 0 0 72
Compensation of employees 44 70 101 624 0 0 0 0 0 0 839
Gross mixed income 7 20 1 166 0 0 0 0 0 0 193
Gross operating surplus 115 19 63 263 0 0 0 0 0 0 460
Total 286 263 576 1971 915 24 366 389 1 483 5273

The different approaches to measuring value-added and GDP from the supply and use tables are shown in Figure 3. The two different methods of measuring value-added and the three different methods of measuring GDP are conceptually equivalent and provide exactly the same values when derived from balanced supply and use tables.

The production approach: provides an estimate of value-added at basic prices as the difference between output and intermediate consumption of each industry. The sum of value-added by all industries plus taxes net of subsidies is equal to GDP at market prices. Often value-added at basic prices is also referred to as GDP at basic prices.

The income approach: also provides an estimate of value-added by industry or for the aggregate economy and can be obtained from summing the contributions of labour and capital to the production process. It is equal to the sum of labour income, gross operating surplus, gross mixed incomeNote 7, and taxes less subsidies on production. Similarly to the production approach, the sum of value-added by all industries plus taxes net of subsidies is equal to GDP at market prices.

The expenditure approach: provides a measure of GDP at market prices for the aggregate economy. It is equal to the sum of the final consumption expenditures of households, Non-Profit Institutions Serving Households (NPISH) and government, gross capital formation, and exports net of imports.

Figure 3 Measurement of value-added and GDP

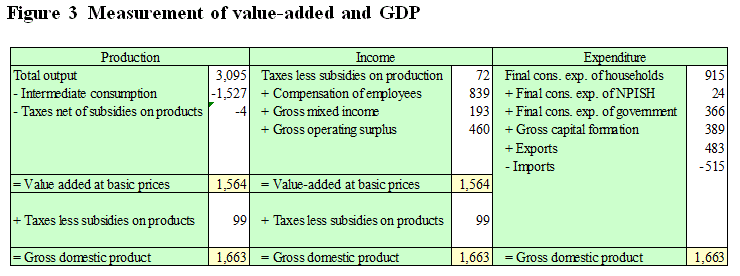
Description for figure 3

Measurement of value added and gross domestic product

This figure provides a numerical example of the three approaches to measuring gross domestic product: the production, income and expenditure approaches. In the production approach, total output (3,095) minus intermediate consumption (-1,527) minus taxes net of subsidies on products (-4) is equal to value added at basic prices (1,564). Value added at basic prices (1,564) plus taxes less subsidies on products (99) is equal to gross domestic product (1,663). In the income approach, taxes less subsidies on production (72) plus compensation of employees (839) plus gross mixed income (193) plus gross operating surplus (460) is equal to value added at basic prices (1,564). Value added at basic prices (1,564) plus taxes less subsidies on products (99) is equal to gross domestic product (1,663). In the expenditure approach, final consumption expenditures of households (915) plus final consumption expenditures of non-profit institutions serving households (24) plus final consumption expenditure of government (366) plus gross capital formation (389) plus exports (483) minus imports (515) is equal to gross domestic product (1,663).

4.2 Direct impact of exports

The direct impacts of exports on industry output are derived by converting exports by product into industry exports through industries' average market shares by product. The direct impact on value-added is subsequently derived by applying industries' value-added coefficients to the output values derived in the first step. These steps are further explained below.

The average product market shares by industry, matrix D, derived from the outputs by industry is shown in Table 4. It is equal to the value of each product output divided by its total output. Taking manufacturing as an example (column 4 of Table 4), Table 2 shows output of manufacturing products by the primary industries out of total output of manufacturing products, 1 / 541 = .001, for the manufacturing industry as 537 / 541 = .99 and for the services industry 3 / 541 = .01.

Table 4
Product market shares, D matrix
Table summary
This table displays the results of Product market shares. The information is grouped by Industries (appearing as row headers), Products, Agriculture and forestry, Mining, Utilities, Construction, Manufacturing and Services, calculated using units units of measure (appearing as column headers).
Industries Products
Agriculture and forestry Mining Utilities Construction Manufacturing Services
units
Primary 0.98 0.99 0.84 0.00 0.00 0.01
Construction 0.00 0.00 0.00 1.00 0.00 0.00
Manufacturing 0.02 0.01 0.01 0.00 0.99 0.02
Services 0.00 0.00 0.15 0.00 0.01 0.98
Total 1.00 1.00 1.00 1.00 1.00 1.00

The input coefficients (or technology functions) of industries are shown in Table 5. These coefficients are derived from the input table and show the amount of inputs required to produce one unit of output. They are derived as the value of inputs divided by total inputs of each industry. The coefficients are split into two matrices, one for intermediate inputs, B, and one for the value-added components; for simplicity in this case only the sum of the value-added components is shown, w. For example, the value-added coefficient of manufacturing is derived from table 3 as the sum of the value-added components divided by the industry's total inputs (2 + 101 + 1 + 63) / 576 = .29.

Table 5
Techonology coefficients
Table summary
This table displays the results of Techonology coefficients. The information is grouped by Products (appearing as row headers), Industries, Primary, Construction, Manufacturing and Services, calculated using B matrix, input coefficients and v vector, value added coefficients units of measure (appearing as column headers).
Products Industries
Primary Construction Manufacturing Services
B matrix, input coefficients
Agriculture and forestry 0.05 0.00 0.05 0.00
Mining 0.06 0.05 0.13 0.00
Utilities 0.01 0.00 0.02 0.01
Construction 0.02 0.00 0.00 0.01
Manufacturing 0.09 0.27 0.34 0.06
Services 0.18 0.23 0.17 0.35
Taxes net of subsidies on products -0.01 0.01 0.00 0.00
Cell with no data vT vector, value added coefficients
Value added at basic prices 0.60 0.43 0.29 0.56
Total 1.00 1.00 1.00 1.00

As discussed in section 3, the formulation Dx, the pre-multiplication of the exports vector x, by the market share matrix D, provides a conversion of exports by product, as they appear in the SUTs, to exports by industry. The first column of Table 6 shows the result of these calculations. Taking the example of the services industry, the sum of an element by element multiplication of the last row of the D matrix by the exports vector, shows (.15 * 2) + (.01 * 264) + (.98 * 115) = 114; the share of the services industry in the production of utilities, manufacturing, and services times the export values of each of these products respectively is the value of exports by the services industry.

Pre-multiplying the exports by industry from Dx by the value-added coefficient of each industry (v) generates an estimate of the direct impact of exports on value-added, shown in the last column of Table 6. For example, the services industry value-added coefficient from v times the industry's exports (.56 x 114) = 65.

Table 6
Direct gross and value-added exports by industry
Table summary
This table displays the results of Direct gross and value-added exports by industry. The information is grouped by Industry (appearing as row headers), Direct exports by industry (Dx) and Direct value added exports by industry (v^Dx), calculated using units units of measure (appearing as column headers).
Industry Direct exports by industry (Dx) Direct value added exports by industry (v^Dx)
units
Primary 103 62
Construction 0 0
Manufacturing 265 77
Services 114 65
Total 483 204

4.3 Total impact of exports

Quantifying the total impact of exports requires going beyond the direct impacts generated in the exporting industry to including all other upstream impacts on economic activity. A schematic view of these interactions is provided in figure 3. Exports by product originate in domestic production and their direct impact on value-added is described in section 4.2. However, purchases of intermediate inputs by the exporting industry are supplied from either imports or a second round of output by domestic producers. Similarly, these second round producers generate value-added and further purchases of domestically produced and imported intermediate inputs. This process can iterate for several rounds until it converges to trivial effects on the economy. In this manner, the value of an export can be fully decomposed into its constituents: the direct and indirect impacts on value-added and the indirect impacts on imports.

The round-by-round impacts described in figure 4 are calculated by tracking the inter-industry transactions required to produce the exports:

i) The market shares matrix, D, allocates the demand for exports to their producing industries.
ii) The intermediate inputs coefficient matrix, B, converts industry outputs into the required demands for intermediate inputs.
iii) The μ matrix derives the imports associated with the demand for intermediates and thus simultaneously the residual demand for output from domestic producers.
iv) The market shares matrix, D, allocates demands for domestic intermediate inputs to their producing industries.
v) Steps ii to iv are repeated until the impacts become trivial. With this method, less than ten iterations usually account for most of the impacts.

Equation (14) formalizes the impact of these iterative steps on industry output. The sum of the power series is merely an approximation of the IO inverse calculated in equation (3).

g* = Dx + D(I−mu)BDx + (D(I−mu)B)(D(I−mu)B)Dx + (D(I−mu)B)3Dx + …      (16)      =[I−D(I−μˆ)B]−1Dx

Figure 4 Total impact of exports

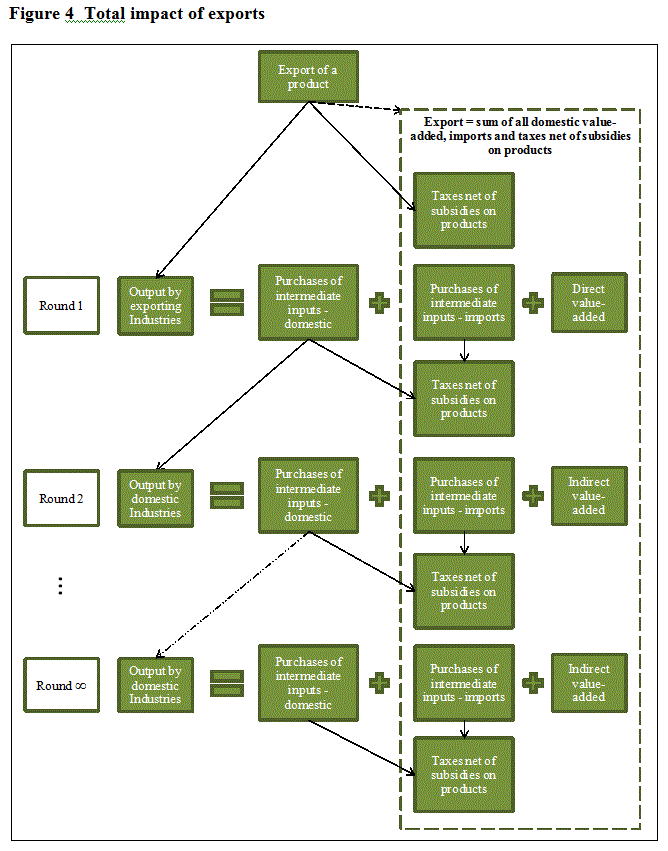
Description for figure 4

Total impact of exports

This diagram shows the decomposition of an exported product into domestic value-added and international imports by tracking round-by-round inter-industry transactions. In round 1, exports by product, net of taxes on products, originate in the output of the exporting industries, which is equal to the purchases of intermediate inputs from domestic producers plus purchases of imported intermediate inputs and direct value-added. In round 2, purchases of intermediate inputs from domestic producers, net of taxes minus subsidies on products, originate in the output of domestic industries, which is equal to the purchases of intermediate inputs from domestic producers plus purchases of imported intermediate inputs and direct value-added. This process can iterate for several rounds until it converges to trivial effects on the economy, which is represented in the figure by round infinity. In this iterative manner, the value of an export can be fully decomposed into its constituents: the sum of all domestic value-added, imports and taxes net of subsidies on products.

It is possible to examine any stage of the process by extracting the impact on industry output of the relevant terms from the right-hand-side of equation (16). Subsequent application of industry coefficients can be used to extend the analysis to other variables. Thus, the vector of value-added coefficients, v, can be applied to the industry outputs generated, g*, to derive the impact on value-added. Similarly, the import shares by industry coefficients vector, ρ, can be used to derive the value of imports.

Average import shares assumption

As discussed in the previous section, intermediate purchases must be allocated between domestic producers and imports. Multiplying the input coefficients by the import shares by product generates the import shares by industry. Table 7 shows the values of μ, the import shares by product vector. The table also shows μˆB, the import shares by product by industry, and their column sums, the vector ρ, which provides the value of total import shares by industry.

The import shares by product measure the observed average proportion of imports in domestic demands. This average however may hide a large heterogeneity in import shares by industryNote 8 and may thus lead to a misallocation of upstream impacts on imports and value-added.

Table 7
Import shares by product and by industry
Table summary
This table displays the results of Mu vector. The information is grouped by Products (appearing as row headers), Industries, calculated using ?' vector, import coefficients by industry units of measure (appearing as column headers).
Products Industries
Primary Construction Manufacturing Services
Cell contain no data µ μˆB
Agriculture and forestry 0.17 0.01 0.00 0.01 0.00
Mining 0.30 0.02 0.02 0.04 0.00
Utilities 0.01 0.00 0.00 0.00 0.00
Construction 0.00 0.00 0.00 0.00 0.00
Manufacturing 0.58 0.05 0.16 0.20 0.03
Services 0.05 0.01 0.01 0.01 0.02
Cell contain no data Cell contain no data ρ' vector, import coefficients by industry
Total 0.16 0.09 0.19 0.25 0.05

Total inter-industry impacts

The values of the IO inverse matrix are shown in Table 8. The matrix tabulates all the upstream impacts on the output of each row industry of deliveries to final demand by the column industry. For example, a one dollar's worth of exports by manufacturing will lead to 20 cents of output by primary industries, 1 cent by construction, 1.20 dollars by manufacturing (inclusive of the original export of 1 dollar's worth) and 33 cents by services.

Table 8
IO inverse
Table summary
This table displays the results of IO inverse. The information is grouped by Industries (appearing as row headers), Industries, Primary, Construction, Manufacturing and Services, calculated using units units of measure (appearing as column headers).
Industries Industries
Primary Construction Manufacturing Services
units
Primary 1.12 0.08 0.20 0.03
Construction 0.02 1.01 0.01 0.02
Manufacturing 0.07 0.16 1.20 0.06
Services 0.30 0.38 0.33 1.51

Multiplying through the columns of the IO inverse by the value of industry exports (from Table 6) generates an estimate of their total upstream impacts on all industries' outputs, as shown in Table 9. Impacts on industries' value-added and imports are derived from the application of the respective industry coefficients to industry output levels. As expected, the sum of impacts on value-added and imports, 368 + 116 = 484, is almost equal to the value of gross exports (Table 3). The difference of one is accounted for by the impact of taxes net of subsidies on products which for the sake of simplicity has been ignored.

As an alternative to weighting the industry outputs, the inverse itself could have been weighted by industry value-added to output coefficients to provide a more direct relationship between a 1 dollar delivery to final demand and the upstream impacts on value-added by industry. This weighting could have been similarly applied to import coefficients or any other variable for which a direct relationship to industry output can be reasonably assumed such as jobs coefficients.

Table 9
Total inter-industry transactions related to exports
Table summary
This table displays the results of Total inter-industry transactions related to exports. The information is grouped by Industries (appearing as row headers), Industries, Primary, Construction, Manufacturing, Services and Total, calculated using units units of measure (appearing as column headers).
Industries Industries
Primary Construction Manufacturing Services Total
units
Output  
Primary 115 0 53 3 171
Construction 2 0 3 3 8
Manufacturing 7 0 317 7 331
Services 31 0 89 173 293
Total 155 1 462 186 803
Value-added  
Primary 69 0 32 2 103
Construction 1 0 1 1 3
Manufacturing 2 0 92 2 96
Services 18 0 50 98 165
Total 90 0 175 103 368
Imports  
Primary 10 0 5 0 15
Construction 0 0 1 0 1
Manufacturing 2 0 81 2 84
Services 2 0 5 9 15
Total 14 0 90 11 116

5. Comparison of VAE to the OECD-WTO Trade in Value-added database

The OECD and WTO have jointly published a Trade in Value-added (TiVA) database (OECD-WTO 2012). The TiVA database is calculated from a world input-output table and provides detail for 40 countries and 18 industries. The world input-output tables allow for the estimation of a large number of analytical variables and geographical detail that cannot be derived from the Canadian input-output tables.

The advantage of a world input-output table is that it allows tracking intermediate inputs as they cross geographic boundaries and industrial processing stages on their destination to foreign or possibly domestic final demands. Thus, the TiVA database tracks foreign value-added by industry and geography, including any recursive impacts on the domestic economy. The main weakness of the TiVA database, however, is the lower precision of its estimates due to the high industrial aggregation level used and the adjustments to national figures required to balance multilateral international trade—which is often contradictory in official statistics—across the different national IO tables.

Unlike the TiVA, the Canadian value-added exports database has no information on activities in the rest-of-the-world and thus cannot track 1) imports and their value-added content by country or 2) exports beyond their initial geographic destination. The VAE is not a tool for tacking the global value-added chain but rather, as its name indicates, it is a tool for tracking the impact of exports on the Canadian economy. Its main comparative advantages though are the greater industrial detail, the greater precision of the available variables, and the availability of additional information on jobs.

In general, the TiVA database is a very useful tool for international comparisons while Statistic's Canada's VAE is more appropriate for analyses that focus on the Canadian economy.

References

Miller and, R.E., and P.D. Blair, 2009, "Input-Output Analysis: Foundations and Extensions," Cambridge University Press, New York.

Organization for Economic Co-operation and Development – World Trade Organization, 2012, "Trade in Value-Added: Concepts, Methodologies and Challenges", OECD, Paris.

United Nations, 2009, System of National Accounts 2008, United Nations, New York.

Notes

Date modified: