4. An application

Jiming Jiang, Thuan Nguyen and J. Sunil Rao

Previous

We consider an application of the methods developed in the previous sections to the TVSFP data. For a complete description of the TVSFP study, see Hedeker, Gibbons and Flay (1994). The original study was designed to test independent and combined effects of a school-based social-resistance curriculum and a television-based program in terms of tobacco use prevention and cessation. The subjects were seventh-grade students from Los Angeles (LA) and San Diego in the State of California in the United States. The students were pretested in January 1986 in an initial study. The same students completed an immediate postintervention questionnaire in April 1986, a one-year follow-up questionnaire (in April 1987), and a two-year follow-up (in April 1988). In this analysis, we consider a subset of the TVSFP data involving students from 28 LA schools, where the schools were randomized to one of four study conditions: (a) a social-resistance classroom curriculum (CC); (b) a media (television) intervention (TV); (c) a combination of CC and TV conditions; and (d) a no-treatment control. A tobacco and health knowledge scale (THKS) score was one of the primary study outcome variables, and the one used for this analysis. The THKS consisted of seven questionnaire items used to assess student tobacco and health knowledge. A student's THKS score was defined as the sum of the items that the student answered correctly. Only data from the pretest and immediate postintervention are available for the current analysis. More specifically, the data only involved subjects who had completed the THKS at both of these time points. On the one hand, the Complete-record data set up an ideal "before-after� situation; on the other hand, the missing data, that is, those from subjects who had completed the questionnaire at only one time point, might have provided additional useful information. For example, it is possible that a subject did not complete the follow-up because he or she did not find the program helpful. Unfortunately, the incomplete data were not available. As a result, there is a potential risk of selection bias for the complete-record-only analysis. In all, there were 1,600 students from the 28 schools, with the number of students from each school ranging from 18 to 137.

Hedeker et al. (1994) carried out a mixed-model analysis based on a number of NER models to illustrate maximum likelihood estimation for the analysis of clustered data. Here we consider a problem of estimating the small area means for the difference between the immediate postintervention and pretest THKS scores (the response). Here the "small area� is understood as a number of major characteristics (e.g., residential area, teacher/student ratio) that affect the response, but are not captured by the covariates in the model (i.e., linear combination of the CC, TV and CCTV indicators). Note that, traditionally, the words "small areas� correspond to small geographical regions or subpopulations, for which adequate samples are not available (e.g., Rao 2003), and such information as residential characteristics or teacher/student ratios would be used as additional covariates. However, such characteristic information are not available. This is why we define these unavailable information as "area-specific�, so that they can be treated as the (small-area) random effects. This is consistent with the fundamental features of the random effects that are often used to capture unobservable effects or information (e.g., Jiang 2007), and extends the traditional notion of small area estimation. Thus, a small area is the seventh graders in all of the U.S. schools that share the similar major characteristics as a LA school involved in the data over a reasonable period of time (e.g., five years) so that these characteristics had not changed much during the time and neither had the social/educational relevance of the CC and TV programs. There are 28 LA schools in the TVSFP data that correspond to 28 sets of characteristics, so that the data are considered random samples from the 28 small areas defined as above. As such, each small area population is large enough so that $n_i/N_i\approx \mathrm{0,1}\le i\le 28.$ Recall that the $n_i’\text{s}$ in the TVSFP sample range from 18 to 137, while the $N_i’\text{s}$ are expected to be at least tens of thousands. Note that the only place in the OBP where the knowledge of $N_i$ is required is through the ratio $n_i/N_i.$ The proposed NER model can be expressed as (1.1) with ${x^{\prime }}_{ij}\beta ={\beta }_0+{\beta }_1{x}_{i\mathrm{,1}}+{\beta }_2{x}_{i\mathrm{,2}}+{\beta }_3{x}_{i\mathrm{,1}}{x}_{i\mathrm{,2}},$ where $x_{i\mathrm{,1}}=1$ if CC, and $0$ otherwise; $x_{i\mathrm{,2}}=1$ if TV, and $0$ otherwise. It follows that all the auxiliary data $x_i$ are at the area level; as a result, the value of ${\overline{X}}_i$ is known for every $i.$

As noted, the sample sizes for some small areas are quite large, but there are also areas with relatively (much) smaller sample sizes. This is quite common in real-life problems. Because the auxiliary data are at area-level, we have ${{\overline{X}}^{\prime }}_i\beta ={{\overline{x}}^{\prime }}_i\beta ;$ thus, it is easy to show that the BP (1.5) can be expressed as

$${\tilde{\theta }}_i=\left\{r_i+\left(1-r_i\right)\frac{n_i\gamma }{1+n_i\gamma }\right\}{\overline{y}}_i+\frac{1-r_i}{1+n_i\gamma }{{\overline{x}}^{\prime }}_i\beta \mathrm{.}$$

It is seen that, when $n_i$ is large, the BP is approximately equal to ${\overline{y}}_i,$ the design-based estimator, which has nothing to do with the parameter estimation. Therefore, when $n_i$ is large, there is not much difference between the OBP and the EBLUP. On the other hand, when $n_i$ is small or moderate, we expect some difference between the OBP and the EBLUP in terms of the MSPE. However, it is difficult to tell how much difference there is in this real data example. Our simulation results in Section 2 show that the difference between OBP and EBLUP in terms of the MSPE depends on to what extent the assumed model is misspecified. It should be noted that the response, $y_{ij},$ is difference in the THKS scores, and possible values of the THKS score are integers between 0 and 7. Clearly, such data is not normal. The potential impact of the nonnormality is two-fold. On the one hand, it is likely that the NER model, as proposed by Hedeker et al. (1994), is misspecified, in which case expression (1.5) is no longer the BP, and the Gaussian ML (REML) estimators are no longer the true ML (REML) estimators. On the other hand, even without the normality, (1.5) can still be justified as the best linear predictor (BLP; e.g., Searle, Casella and McCulloch 1992, Section 7.3). Furthermore, the Gaussian ML (REML) estimators are consistent and asymptotically normal even without the normality assumption (Jiang 1996; also see Jiang 2007, Chapter 1). 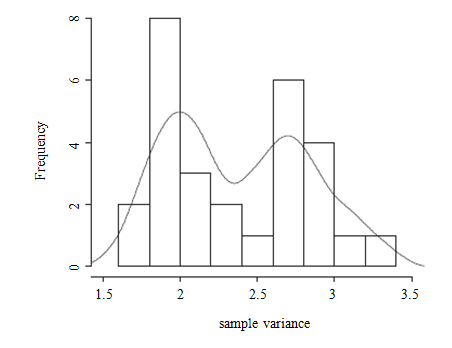Other aspects of the NER model include homoscedasticity of the error variance across the small areas. Figure 4.1 shows the histogram of the sample variances of the 28 small areas. The bimodal shape of the histogram suggests potential heteroscedasticity in the error variance, yet another type of possible model misspecification. Therefore, the OBP method is naturally considered.

Figure 4.1 Histogram of sample variances; a kernel density smoother is fitted.

Description for Figure 4.1

We carry out the OBP analysis for the 28 small areas and the results are presented in Table 4.1. The BPE of the parameters are ${\widehat{\beta }}_0=0.206,{\widehat{\beta }}_1=0.687,$   ${\widehat{\beta }}_2=0.213,{\widehat{\beta }}_3=-0.288,$  and $\widehat{\gamma }=\mathrm{0.003.}$  Although interpretation may be given for the parameter estimates, there is a concern about possible model misspecification (in which case the interpretation may not be sensible), as noted earlier. Regardless, our main interest is prediction, not estimation; thus, we focus on the OBP. In addition to the OBPs, we also computed the corresponding $\widehat{\text{MSPE}},$  and their square roots as the measures of uncertainty. As a comparison, the EBLUPs for the small areas as well as the corresponding square roots of the MSPE estimates, $\widetilde{\text{MSPE}},$  using the Prasad-Rao method $(\text{P}-\text{R};$  Prasad and Rao 1990) are also included in the table. It is seen that the OBPs are all positive, even for the small areas in the control group. As for the statistical significance (here "significance� is defined as that the OBP is greater in absolute value than 2 times the corresponding square root of the MSPE estimate), the small area means are significantly positive for all of the small areas in the (1,1) group. In contrast, none of the small area mean is significantly positive for the small areas in the (0,0) group. As for the other two groups, the small area means are significantly positive for all the small areas in the (1,0) group; the small area means are significantly positive for all but two small areas in the (0,1) group. There are 7, 8, 7 and 7 small areas in the (0,0), (0,1), (1,0) and (1,1) groups, respectively.

Table 4.1
OBP, EBLUP, measures of uncertainty for TVSFP data (Part 1)
Table summary
This table displays the results of OBP. The information is grouped by ID (appearing as row headers), CC, TV, OBP, $\sqrt{\widehat{\text{MSPE}}}$ , EBLUP and $\sqrt{\widetilde{\text{MSPE}}}$ (appearing as column headers).

ID	CC	TV	OBP	$\sqrt{\widehat{\text{MSPE}}}$	EBLUP	$\sqrt{\widetilde{\text{MSPE}}}$
403	1	0	0.886	0.171	0.913	0.121
404	1	1	0.844	0.296	0.856	0.121
193	0	0	0.215	0.207	0.217	0.120
194	0	0	0.221	0.137	0.221	0.134
196	1	0	0.878	0.171	0.907	0.124
197	0	0	0.225	0.158	0.223	0.126
198	1	1	0.771	0.220	0.807	0.131
199	0	1	0.426	0.142	0.453	0.130
401	1	1	0.826	0.133	0.844	0.127
402	0	0	0.188	0.171	0.199	0.123
405	0	1	0.394	0.147	0.432	0.129
407	0	1	0.508	0.300	0.508	0.133
408	1	0	0.871	0.240	0.903	0.123
409	0	0	0.230	0.125	0.227	0.136

Table 4.2
OBP, EBLUP, measures of uncertainty for TVSFP data (Part 2)
Table summary
This table displays the results of OBP. The information is grouped by ID (appearing as row headers), CC, TV, OBP, $\sqrt{\widehat{\text{MSPE}}}$, EBLUP, and $\sqrt{\widetilde{\text{MSPE}}}$ (appearing as column headers).

ID	CC	TV	OBP	$\sqrt{\widehat{\text{MSPE}}}$	EBLUP	$\sqrt{\widetilde{\text{MSPE}}}$
410	1	1	0.778	0.304	0.813	0.124
411	0	1	0.409	0.195	0.444	0.115
412	1	0	0.913	0.219	0.930	0.126
414	1	0	0.929	0.257	0.941	0.127
415	1	1	0.869	0.199	0.872	0.135
505	1	1	0.790	0.154	0.818	0.136
506	0	1	0.389	0.169	0.428	0.134
507	0	1	0.426	0.148	0.452	0.135
508	0	1	0.411	0.108	0.442	0.136
509	1	0	0.915	0.097	0.929	0.143
510	1	0	0.880	0.119	0.905	0.143
513	0	0	0.185	0.215	0.197	0.123
514	1	1	0.866	0.144	0.870	0.140
515	0	0	0.180	0.102	0.192	0.143

Comparing the OBP with the EBLUP, the values of the latter are generally higher, and their corresponding MSPE estimates are mostly lower. In terms of statistical significance, the EBLUP results are significant for the (1,1), (1,0) and (0,1) groups, and insignificant for the (0,0) group. It should be noted that the $\text{P}-\text{R}$ MSPE estimator for the EBLUP is derived under the normality assumption, while in this case the data is clearly not normal, as noted earlier. Thus, the measure of uncertainty for the EBLUP may not be accurate. In particular, just because the (square roots of the) MSPEs for the EBLUPs are lower, compared to those for the OBPs, it does not mean the corresponding true MSPEs for the EBLUPs are lower than those for the OBPs. In fact, our simulation results (see Section 2) have shown otherwise. It is also observed that the MSPE estimates for the EBLUPs are more homogeneous cross the small areas. This may be due to the fact that the $\text{P}-\text{R}$ MSPE estimator for EBLUP is obtained assuming that the NER model is correct, while the proposed MSPE estimator for OBP does not use such an assumption.

In conclusion, in spite of the potential difference in the small area characteristics, the CC and TV programs appear to be successful in terms of improving the students' THKS scores (whether the improved THKS score means improved tobacco use prevention and cessation is a different matter though). It also seems apparent that the CC program was relatively more effective than the TV program. Without the intervention of any of these programs, the THKS score did not seem to improve in terms of the small area means. In terms of the statistically significant results, when CC = 0 and TV = 0, the THKS score did not seem to improve; when CC = 1, the THKS score seemed to improve; and, when CC = 0 and TV = 1, the improvement of the THKS score was not so convincing.

Acknowledgements

Jiming Jiang is partially supported by the NSF grants DMS-0809127 and SES-1121794. Thuan Nguyen is partially supported by the NSF grant SES-1118469. J. Sunil Rao is partially supported by the NSF grants DMS-0806076 and SES-1122399. The research of all three authors are partially supported by the NIH grant R01-GM085205A1. The authors thank Professor Donald Hedeker for kindly providing the TVSFP data for our analysis. Finally, the authors are grateful to the comments made by an Associate Editor and two referees.

Appendix

A.1. OBP under nested-error regression. The design-based MSPE is given by (1.6). Note that all the $\text{E},$ and later $\text{P},$ are design-based, assuming simple random sampling. Note that $\text{E}{\left\{{\tilde{\theta }}_i\left(\psi \right)-{\theta }_i\right\}}^2=\text{E}\left\{{\tilde{\theta }}_i^2\left(\psi \right)\right\}-2{\theta }_i\text{E}\left\{{\tilde{\theta }}_i\left(\psi \right)\right\}+{\theta }_i^2.$ Furthermore, note that $\text{E}\left({\overline{y}}_{i\cdot }\right)={\theta }_i$ and $\text{E}\left({\overline{x}}_{i\cdot }\right)={\overline{X}}_i$ $({\overline{y}}_{i\cdot }$ and ${\overline{x}}_{i\cdot }$ are design-unbiased estimators of their corresponding subpopulation means). Thus, we have

$$\begin{array}{ll}\text{E}\left\{{\tilde{\theta }}_i\left(\psi \right)\right\}\hfill & ={{\overline{X}}^{\prime }}_i\beta +\left\{\frac{n_i}{N_i}+\left(1-\frac{n_i}{N_i}\right)\frac{n_i{\sigma }_v^2}{{\sigma }_e^2+n_i{\sigma }_v^2}\right\}\left({\theta }_i-{{\overline{X}}^{\prime }}_i\beta \right)\hfill \\ \hfill & =\left(1-\frac{n_i}{N_i}\right)\frac{{\sigma }_e^2}{{\sigma }_e^2+n_i{\sigma }_v^2}{{\overline{X}}^{\prime }}_i\beta +\left\{\frac{n_i}{N_i}+\left(1-\frac{n_i}{N_i}\right)\frac{n_i{\sigma }_v^2}{{\sigma }_e^2+n_i{\sigma }_v^2}\right\}{\theta }_i\mathrm{.}\hfill \end{array}$$

Thus, using the notation introduced below (1.7), we have

$$\text{E}{\left\{{\tilde{\theta }}_i\left(\psi \right)-{\theta }_i\right\}}^2=\text{E}\left\{{\tilde{\theta }}_i^2\left(\psi \right)\right\}-2\frac{1-r_i}{1+n_i\gamma }{{\overline{X}}^{\prime }}_i\beta {\theta }_i+b_i\left(\gamma \right){\theta }_i^2\mathrm{.}\left(\text{A}.1\right)$$

We can express the unknown ${\theta }_i$ in (A.1) by $\text{E}\left({\overline{y}}_{i\cdot }\right).$ We also need a design-based unbiased estimator of ${\theta }_i^2,$ which is given by (1.8). In other words, we have ${\theta }_i^2=\text{E}\left({\widehat{\mu }}_i^2\right).$ To show the design-unbiasedness of (1.8), note that

$$\begin{array}{ll}\text{E}\left(\frac{1}{n_i}{\displaystyle \sum _{j=1}^{n_i}{y}_{ij}^2}\right)\hfill & =\frac{1}{n_i}\text{E}\left\{{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2{1}_{\left(k\in I_i\right)}}\right\}\hfill \\ \hfill & =\frac{1}{n_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2\text{P}\left(k\in I_i\right)}=\frac{1}{N_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}\mathrm{,}\hfill \end{array}$$

where $I_i$ is the set of sampled indexes corresponding to the $i^{\text{th}}$ small area. Also, we have

$$\begin{array}{ll}\text{E}\left\{\frac{N_i-1}{N_i\left(n_i-1\right)}{\displaystyle \sum _{j=1}^{n_i}}{\left(y_{ij}-{\overline{y}}_{i\cdot }\right)}^2\right\}\hfill & =\frac{N_i-1}{N_i\left(n_i-1\right)}\text{E}\left({\displaystyle \sum _{j=1}^{n_i}{y}_{ij}^2}-n_i{\overline{y}}_{i\cdot }^2\right)\hfill \\ \hfill & =\frac{N_i-1}{N_i\left(n_i-1\right)}\text{E}\left({\displaystyle \sum _{j=1}^{n_i}{y}_{ij}^2}\right)-\frac{\left(N_i-1\right)n_i}{N_i\left(n_i-1\right)}\text{E}\left({\overline{y}}_{i\cdot }^2\right)\hfill \\ \hfill & =\frac{\left(N_i-1\right)n_i}{N_i\left(n_i-1\right)}\left\{\frac{1}{N_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}-\text{E}\left({\overline{y}}_{i\cdot }^2\right)\right\}\mathrm{,}\hfill \end{array}$$

and

$$\begin{array}{ll}\text{E}\left({\overline{y}}_{i\cdot }^2\right)\hfill & =\frac{1}{n_i^2}\text{E}{\left\{{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}{1}_{\left(k\in I_i\right)}}\right\}}^2\hfill \\ \hfill & =\frac{1}{n_i^2}{\displaystyle \sum _{k\mathrm{,}l=1}^{N_i}{Y}_{ik}{Y}_{il}\text{P}\left(k\in I_i\mathrm{,}l\in I_i\right)}\hfill \\ \hfill & =\frac{1}{n_i^2}\left\{{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2\frac{n_i}{N_i}}+{\displaystyle \sum _{k\ne l}{Y}_{ik}{Y}_{il}\frac{n_i\left(n_i-1\right)}{N_i\left(N_i-1\right)}}\right\}\hfill \\ \hfill & =\frac{1}{n_i^2}\left[\frac{n_i}{N_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}+\frac{n_i\left(n_i-1\right)}{N_i\left(N_i-1\right)}\left\{{\left({\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}}\right)}^2-{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}\right\}\right]\hfill \\ \hfill & =\frac{1}{n_i^2}\left\{\frac{n_i\left(N_i-n_i\right)}{N_i\left(N_i-1\right)}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}+\frac{N_i{n}_i\left(n_i-1\right)}{N_i-1}{\theta }_i^2\right\}\hfill \\ \hfill & =\frac{N_i-n_i}{N_i\left(N_i-1\right)n_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}+\frac{N_i\left(n_i-1\right)}{\left(N_i-1\right)n_i}{\theta }_i^2\mathrm{.}\hfill \end{array}$$

Thus, after combining things together, we get

$$\text{E}\left({\widehat{\mu }}_i^2\right)=\left[1-\frac{\left(N_i-1\right)n_i}{N_i\left(n_i-1\right)}\left\{1-\frac{N_i-n_i}{\left(N_i-1\right)n_i}\right\}\right]\left(\frac{1}{N_i}{\displaystyle \sum _{k=1}^{N_i}{Y}_{ik}^2}\right)+{\theta }_i^2={\theta }_i^2\mathrm{.}$$

It follows that the right side of (A.1) can be expressed as

$$\text{E}\left[{\displaystyle \sum _{i=1}^m}\left\{{\tilde{\theta }}_i^2\left(\psi \right)-2\frac{1-r_i}{1+n_i\gamma }{{\overline{X}}^{\prime }}_i\beta {\overline{y}}_{i\cdot }+b_i\left(\gamma \right){\widehat{\mu }}_i^2\right\}\right]\mathrm{.}$$

The BPE is obtained by minimizing the expression inside the expectation, which is (1.7).

References

Battese, G.E., Harter, R.M. and Fuller, W.A. (1988). An error-components model for prediction of county crop areas using survey and satellite data. Journal of the American Statistical Association, 83, 401, 28-36.

Chatterjee, S., Lahiri, P. and Li, H. (2008). Parametric bootstrap approximation to the distribution of EBLUP and related prediction intervals in linear mixed models. The Annals of Statistics, 36, 3, 1221-1245.

Datta, G.S., Kubokawa, T., Molina, I. and Rao, J.N.K. (2011). Estimation of mean squared error of model-based small area estimators. Test, 20, 367-388.

Efron, B. (1979). Bootstrap method: Another look at the jackknife. The Annals of Statistics, 7, 1, 1-26.

Efron, B., and Tibshirani, R.J. (1993). An Introduction to the Bootstrap, Chapman & Hall/CRC.

Fay, R.E., and Herriot, R.A. (1979). Estimates of income for small places: An application of James-Stein procedures to census data. Journal of the American Statistical Association, 74, 366a, 269-277.

Hall, P., and Maiti, T. (2006). Nonparametric estimation of mean-squared prediction error in nested-error regression models. The Annals of Statistics, 34, 4, 1733-1750.

Hedeker, D., Gibbons, R.D. and Flay, B.R. (1994). Random-effects regression models for clustered data with an example from smoking prevention research. Journal of Consulting and Clinical Psychology, 62, 4, 757-765.

Jiang, J. (1996). REML estimation: Asymptotic behavior and related topics. The Annals of Statistics, 24, 1, 255-286.

Jiang, J. (2007). Linear and Generalized Linear Mixed Models and Their Applications, New York: Springer.

Jiang, J., and Nguyen, T. (2012). Small area estimation via heteroscedastic nested-error regression. The Canadian Journal of Statistics/La revue canadienne de statistique, 40, 3, 588-603.

Jiang, J., Lahiri, P. and Wan, S.-M. (2002). A unified jackknife theory for empirical best prediction with estimation. The Annals of Statistics, 30, 6, 1782-1810.

Jiang, J., Nguyen, T. and Rao, J.S. (2011). Best predictive small area estimation. Journal of the American Statistical Association, 106, 494, 732-745.

Lahiri, P. (2012). Estimation of average design-based mean squared error of synthetic small area estimators. Presented at the 40th Annual Meeting of the Statistical Society of Canada, Guelph, ON.

Nandram, B., and Sun, Y. (2012). A Bayesian model for small area under heterogeneous sampling variances. Technical Report.

Prasad, N.G.N., and Rao, J.N.K. (1990). The estimation of mean squared errors of small area estimators. Journal of the American Statistical Association, 85, 409, 163-171.

Rao, J.N.K. (2003). Small Area Estimation, New York: John Wiley & Sons, Inc.

Searle, S.R., Casella, G. and McCulloch, C.E. (1992). Variance Components, New York: John Wiley & Sons, Inc.

Torabi, M., and Rao, J.N.K. (2012). Estimation of mean squared error of model-based estimators of small area means under a nested error linear regression model. Technical Report.

Previous