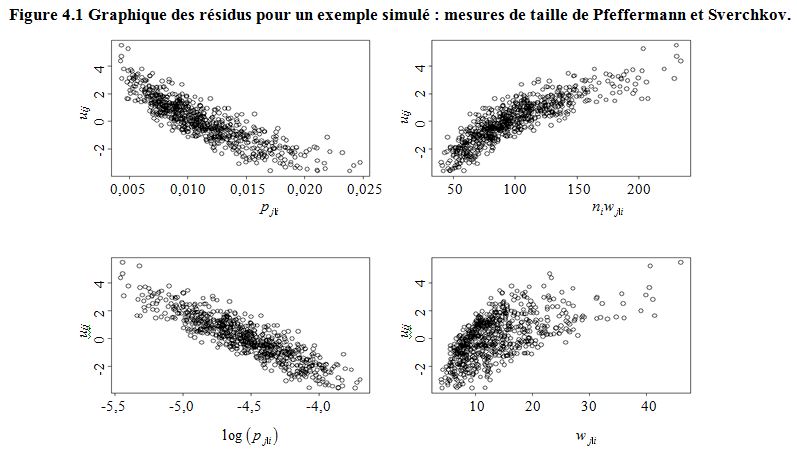
Estimation sur petits domaines fondée sur un modèle sous échantillonnage informatif 4. Étude en simulationEstimation sur petits domaines fondée sur un modèle sous échantillonnage informatif 4. Étude en simulation

• Précédent
• Suivant

4.1 Exécution

Une approche plan de sondage-modèle (pm) a été utilisée pour l’étude en simulation en générant des données pour les $N={\displaystyle {\sum }_{i=1}^M{N}_i}$ unités de la population conformément à un modèle spécifié, puis en sélectionnant un échantillon selon un plan de sondage spécifié. Le processus de génération des données de la population, puis de sélection d’un échantillon a été répété $R$ fois. Nous décrivons maintenant les étapes de l’exécution du processus. Les données de population, $y_{ij},$ pour $M=99$ domaines et $N_i=100$ unités dans chaque domaine $i$ ont été générées au moyen du simple modèle de régression linéaire à erreurs emboîtées

$$y_{ij}={\beta }_0+{\beta }_1{x}_{ij}+{\nu }_i+e_{ij};i=1,\dots ,99;j=1,\dots ,100,(4.1)$$

où ${\beta }_0=1,{\beta }_1=1,v_i\stackrel{\text{iid}}{\sim }N\left(0,{\sigma }_v^2=\text{0,5}\right)$ et indépendants des $e_{ij}\stackrel{\text{iid}}{\sim }N\left(0,{\sigma }_e^2=2\right).$ Les valeurs de $x_{ij}$ dans la population ont été générées à partir d’une loi gamma de moyenne 10 et de variance 50, et maintenues fixes pendant la simulation des valeurs de $y_{ij}$ de la population au moyen de (4.1).

Nous avons considéré différentes tailles d’échantillon dans les domaines en fixant $n_i=5$ pour les 33 premiers domaines, $n_i=7$ pour les 33 domaines suivants et $n_i=9$ pour les 33 derniers domaines. L’objectif était d’étudier l’effet de tailles d’échantillon inégales sur le choix de la variable d’augmentation $g_{ij}=g\left(p_{j|i}\right).$ Des échantillons de tailles spécifiées, $n_i,$ ont été sélectionnés dans les domaines avec probabilités proportionnelles aux tailles spécifiées, $b_{ij},$ en utilisant la méthode d’échantillonnage de Rao-Sampford (Rao 1965 et Sampford 1967) avec probabilités inégales et sans remise. Cette dernière méthode fait en sorte que les probabilités d’inclusion ${\pi }_{j|i}$ soient proportionnelles aux tailles $b_{ij},$ c’est-à-dire, ${\pi }_{j|i}=n_i{b}_{ij}/B_i=n_i{p}_{j|i},j=1,\dots ,N_i,$ où $B_i$ est le total des $b_{ij}$ dans le domaine $i.$

Nous avons considéré deux choix distincts des tailles $b_{ij}$ dans l’étude en simulation. Comme premier choix, nous avons utilisé

$$\begin{array}{lll}{b}_{ij}\hfill & =\hfill & \exp \left[\left\{-\left(y_{ij}-{\beta }_0-{\beta }_1{x}_{ij}\right)/{\sigma }_e+{\delta }_{ij}/5\right\}/3\right]\hfill \\ \hfill & =\hfill & \exp \left[\left\{-\left(v_i+e_{ij}\right)/{\sigma }_e+{\delta }_{ij}/5\right\}/3\right],\hfill \end{array}(4.2)$$

où ${\delta }_{ij}\stackrel{\text{iid}}{\sim }N\left(\text{0,1}\right).$ Les mesures de taille (4.2) sont équivalentes à celles utilisées par Pfeffermann et Sverchkov (2007) dans leur étude en simulation et satisfont la relation (1.2) sur les poids $w_{j|i}={\pi }_{j|i}^{-1}.$ À l’instar de l’approche PS, nous avons tronqué les effets de domaine $v_i$ et les erreurs au niveau de l’unité $e_{ij}$ à $\pm \text{2,5}{\sigma }_v$ et $\pm \text{2,5}{\sigma }_e$ pour éviter des probabilités de sélection extrêmes.

Le deuxième choix de mesures de taille, à l’exemple d’Asparouhov (2006), comprend deux types distincts de mesure de taille, à savoir une mesure invariante (I) et une mesure non invariante (NI). Dans le cas invariant, $b_{ij}$ est indépendante de $v_i$ sachant $x_{ij};$ sinon, la mesure est dite non invariante. Les mesures de taille invariantes sont données par

$$b_{ij}={\left[1+\exp \left\{-\tau \left(\frac{1}{\alpha }{e}_{ij}+\sqrt{1-\frac{1}{{\alpha }^2}}{e}_{ij}^{*}\right)\right\}\right]}^{-1}.(4.3)$$

Les mesures de taille non invariantes sont telles que

$$b_{ij}={\left[1+\exp \left\{-\tau \left(\frac{1}{\alpha }\left(v_i+e_{ij}\right)+\sqrt{1-\frac{1}{{\alpha }^2}}\left(v_i^{*}+e_{ij}^{*}\right)\right)\right\}\right]}^{-1}.(4.4)$$

Le coefficient $\tau$ dans (4.3) et (4.4), qui est choisi égal à 0,5, fait en sorte que la variation des poids $w_{j|i}$ ne soit pas trop grande dans une exécution de la simulation. La paire aléatoire $\left(v_i^{*},e_{ij}^{*}\right)$ a été générée indépendamment de $\left(v_i,e_{ij}\right)$ à partir des mêmes lois que celle de $v_i$ et $e_{ij}$ pour s’assurer que la variation des poids soit comparable entre les divers niveaux de $\alpha .$ Les probabilités ${\pi }_{j|i}$ qui étaient supérieures à un ont été fixées à un, et les probabilités des unités restantes ont été recalculées. Les valeurs de $\alpha$ dans (4.3) et (4.4), choisies égales à 1, 2, 3 ou $\infty ,$ contrôlent le niveau d’informativité (caractère informatif). L’accroissement de la valeur de $\alpha$ réduit l’informativité, $\alpha =\infty$ correspondant à un échantillonnage non informatif. Diverses dépendances ont été introduites dans les simulations comme il suit, afin d’accroître la précision des comparaisons entre les différents estimateurs : les quatre composantes de l’erreur $\left(v_i,e_{ij},v_i^{*},e_{ij}^{*}\right)$ ont toutes été générées pour commencer. Les valeurs de $y$ dans la population, ainsi que les probabilités de sélection invariantes et non invariantes, ont ensuite été générées à partir de ces erreurs. Pour une population générée donnée, huit échantillons ont été sélectionnés : un échantillon invariant et un échantillon non invariant pour chaque valeur de $\alpha$ prise en considération.

Il convient de souligner que les poids $w_{j|i}$ obtenus au moyen des mesures de taille (4.3) et (4.4) peuvent ne pas satisfaire la condition (1.2) de l’approche PS. Nous avons néanmoins ajusté (1.2) à ces poids pour calculer $\widehat{b},$ qui est nécessaire afin de calculer l’estimateur corrigé du biais ${\widehat{\overline{Y}}}_i^{\text{PS}}.$

En utilisant l’approche plan de sondage-modèle (pm), nous avons généré $R=\text{1}\text{000}$ échantillons sous les mesures de taille (4.2) et sous les mesures de taille (4.3) et (4.4). Pour chaque échantillon simulé $r\left(r=1,\dots ,R\right),$ nous avons calculé les estimations ${\widehat{\overline{Y}}}_i^{H\left(r\right)},{\widehat{\overline{Y}}}_{i\left(a\right)}^{H\left(r\right)}$ et ${\widehat{\overline{Y}}}_i^{\text{PS}\left(r\right)}$ pour chaque petit domaine $i;$ pour la méthode YR, nous avons calculé ${\widehat{\mu }}_i^{\text{YR}\left(r\right)}$ et ${\widehat{\mu }}_{i\left(a\right)}^{\text{YR}\left(r\right)}$ seulement. En outre, nous avons calculé les estimations de l’EQM, $\text{eqm}{\left({\widehat{\mu }}_i^H\right)}^{\left(r\right)},\text{eqm}{\left({\widehat{\mu }}_{i\left(a\right)}^H\right)}^{\left(r\right)},\text{eqm}{\left({\widehat{\mu }}_i^{\text{YR}}\right)}^{\left(r\right)}$ et $\text{eqm}{\left({\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}\right)}^{\left(r\right)},$ associées à ${\widehat{\mu }}_i^H,{\widehat{\mu }}_{i\left(a\right)}^H,{\widehat{\mu }}_i^{\text{YR}}$ et ${\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}$ . Comme nous l’avons mentionné plus haut, nous n’avons pas inclus l’estimateur bootstrap de l’EQM de ${\widehat{\overline{Y}}}_i^{\text{PS}},$ proposé par Pfeffermann et Sverchkov (2007), dans l’étude en simulation. En outre, pour simplifier, nous n’avons pas inclus les estimateurs de l’EQM de ${\widehat{\overline{Y}}}_i^H$ et ${\widehat{\overline{Y}}}_{i\left(a\right)}^H,$ parce que ces estimateurs donnent des résultats comparables à ${\widehat{\mu }}_i^H$ et ${\widehat{\mu }}_{i\left(a\right)}^H$ en ce qui concerne l’EQM.

Nous avons considéré les mesures de performance qui suivent pour un estimateur donné, disons de la moyenne de petit domaine ${\overline{Y}}_i.$ Le biais absolu moyen $\left(\overline{\text{BA}}\right)$ est mesuré par

$$\overline{\text{BA}}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{\text{BA}}_i}$$

avec

$${\text{BA}}_i=\left|\frac{1}{R}{\displaystyle \sum _{r=1}^R\left({\widehat{\overline{Y}}}_i^{\left(r\right)}-{\overline{Y}}_i^{\left(r\right)}\right)}\right|$$

où ${\widehat{\overline{Y}}}_i^{\left(r\right)}$ et ${\overline{Y}}_i^{\left(r\right)}$ sont les valeurs de ${\widehat{\overline{Y}}}_i$ et ${\overline{Y}}_i$ pour les $r^{\text{e}}$ échantillon et population simulés. L’efficacité d’un estimateur ${\widehat{\overline{Y}}}_i$ est mesurée par la racine carrée moyenne de l’EQM

$$\overline{\text{REQM}}=\frac{1}{M}{\displaystyle \sum _{i=1}^M\sqrt{\frac{1}{R}{\displaystyle \sum _{r=1}^R{\left({\widehat{\overline{Y}}}_i^{\left(r\right)}-{\overline{Y}}_i^{\left(r\right)}\right)}^2}}}.$$

En ce qui concerne la performance des estimateurs de l’EQM, $\text{eqm}\left({\widehat{\mu }}_i^H\right),\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^H\right),\text{eqm}\left({\widehat{\mu }}_i^{\text{YR}}\right)$ et $\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}\right),$ nous avons d’abord calculé des mesures fiables des EQM en passant de $R=\text{1}\text{000}$ à $T=\text{10}\text{000}$ échantillons simulés. L’EQM d’un estimateur ${\widehat{\mu }}_i$ est alors calculée comme il suit

$$\text{EQM}\left({\widehat{\mu }}_i\right)=\frac{1}{T}{\displaystyle \sum _{t=1}^T{\left({\widehat{\mu }}_i^{\left(t\right)}-{\overline{Y}}_i^{\left(t\right)}\right)}^2},$$

où ${\widehat{\mu }}_i^{\left(t\right)}$ ${\overline{Y}}_i^{\left(t\right)}$ désignent les valeurs de ${\widehat{\mu }}_i$ et ${\overline{Y}}_i$ pour les $t^{\text{e}}$ échantillon et population simulés. Pour l’estimation de l’EQM, nous avons gardé les $R$ échantillons simulés originaux et calculé les valeurs prévues $E\left[\text{eqm}\left({\widehat{\mu }}_i\right)\right]=R^{-1}{\displaystyle {\sum }_{r=1}^R\text{eqm}{\left({\widehat{\mu }}_i\right)}^{\left(r\right)}},$ où $\text{eqm}{\left({\widehat{\mu }}_i\right)}^{\left(r\right)}$ désigne la valeur de l’estimation de l’EQM pour le $r^{\text{e}}$ échantillon simulé. Le biais relatif absolu moyen $\left(\overline{\text{BRA}}\right)$ d’un estimateur de l’EQM $\text{eqm}\left({\widehat{\mu }}_i\right)$ est alors calculé selon

$$\overline{\text{BRA}}\left[\text{eqm}\left({\widehat{\mu }}_i\right)\right]=M^{-1}{\displaystyle \sum _{i=1}^M\left|\frac{E\left[\text{eqm}\left({\widehat{\mu }}_i\right)\right]}{\text{EQM}\left({\widehat{\mu }}_i\right)}-1\right|}.$$

4.2 Résultats sous les mesures de taille de Pfeffermann et Sverchkov

Le tableau 4.1 donne les résultats des simulations concernant le biais absolu moyen $\left(\overline{\text{BA}}\right)$ et la racine carrée moyenne de l’erreur quadratique moyenne $\left(\overline{\text{REQM}}\right)$ des estimateurs ${\widehat{\overline{Y}}}_i^H,{\widehat{\overline{Y}}}_{i\left(a\right)}^H,{\widehat{\mu }}_i^{\text{YR}},{\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}$ et ${\widehat{\overline{Y}}}_i^{\text{PS}}$ sous les mesures de taille (4.2) de l’approche PS. Le biais relatif absolu moyen $\left(\overline{\text{BRA}}\right)$ des estimateurs de l’EQM, $\text{eqm}\left({\widehat{\mu }}_i^H\right),\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^H\right),\text{eqm}\left({\widehat{\mu }}_i^{\text{YR}}\right)$ et $\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}\right),$ est également présenté. Quatre choix différents de la variable d’augmentation $g_{ij}$ ont été étudiés : $p_{j|i},w_{j|i},n_i{w}_{j|i}=p_{j|i}^{-1}$ et $\log p_{j|i}.$ L’estimateur bootstrap de $\text{EQM}\left({\widehat{\overline{Y}}}_i^{\text{PS}}\right)$ proposé par Pfeffermann et Sverchkov (2007) n’est pas inclus dans notre étude, parce que la simulation bootstrap est très gourmande en ressources informatiques.

Le tableau 4.1 montre que le $\overline{\text{BA}}$ de l’estimateur EBLUP ${\widehat{\overline{Y}}}_i^H$ est grand (= 0,456) comparativement à l’EBLUP avec modèle augmenté correspondant, ${\widehat{\overline{Y}}}_{i\left(a\right)}^H,$ pour les quatre choix de $g_{ij}.$ En outre, le choix $g_{ij}=w_{j|i}$ donne un $\overline{\text{BA}}$ plus grand que les trois autres choix (0,131 comparativement à 0,042 ou moins). Le pseudo-EBLUP habituel, ${\widehat{\mu }}_i^{\text{YR}},$ donne des résultats étonnamment bons $\left(\overline{\text{BA}}=\text{0,044}\right),$ même s’il a été obtenu sous l’hypothèse d’un échantillonnage non informatif. Cette bonne performance est peut-être due à l’utilisation de poids dans ${\widehat{\mu }}_i^{\text{YR}}.$ Le pseudo-EBLUP augmenté, ${\widehat{\mu }}_{i\left(a\right)}^{\text{YR}},$ entraîne une réduction supplémentaire du $\overline{\text{BA}}.$ L’estimateur PS, ${\widehat{\overline{Y}}}_i^{\text{PS}},$ donne de bons résultats comparativement à ${\widehat{\overline{Y}}}_{i\left(a\right)}^H:\overline{\text{BA}}=\text{0,033}.$

Si l’on examine la $\overline{\text{REQM}},$ le tableau 4.1 montre que ${\widehat{\overline{Y}}}_i^H$ possède la plus grande valeur (= 0,617) en raison de son grand $\overline{\text{BA}},$ suivi par ${\widehat{\mu }}_i^{\text{YR}}$ et ${\widehat{\overline{Y}}}_i^{\text{PS}}$ pour lesquels les valeurs sont 0,442 et 0,416, respectivement. Par ailleurs, les estimateurs avec modèle augmenté donnent des résultats significativement meilleurs que ${\widehat{\overline{Y}}}_i^{\text{PS}}$ et ${\widehat{\mu }}_i^{\text{YR}}.$ Par exemple, le choix $g_{ij}=p_{j|i}$ donne $\overline{\text{REQM}}=\text{0,151}.$ Parmi les quatre choix de $g_{ij},$ le choix $w_{j|i}$ donne la plus grande $\overline{\text{REQM}}\left(=\text{0,242}\right).$ Nous avons également calculé le $\overline{\text{BA}}$ et la $\overline{\text{REQM}}$ des estimateurs EBLUP approximatifs ${\widehat{\mu }}_i^H$ et ${\widehat{\mu }}_{i\left(a\right)}^H.$ Nous avons constaté que les valeurs sont presque les mêmes que les valeurs correspondantes pour ${\widehat{\overline{Y}}}_i^H$ et ${\widehat{\overline{Y}}}_{i\left(a\right)}^H.$

Enfin, en ce qui concerne l’estimation de l’EQM, $\text{eqm}\left({\widehat{\mu }}_i^H\right)$ produit le $\overline{\text{BRA}}$ le plus grand, soit 53,1 % comparativement à 3,8 % pour ${\widehat{\mu }}_i^{\text{YR}},$ quoique la $\overline{\text{REQM}}$ de ${\widehat{\mu }}_i^{\text{YR}}$ est plus grande que celle de ${\widehat{\mu }}_{i\left(a\right)}^H$ en se basant sur $p_{j|i}$ ou $n_i{w}_{j|i}.$ Les estimateurs de l’EQM $\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^H\right)$ et $\text{eqm}\left({\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}\right)$ donnent un petit $\overline{\text{BRA}}\left(<7\%\right),$ sauf pour le choix $w_{j|i}$ qui donne $\overline{\text{BRA}}=\text{62,6}\%$ pour ${\widehat{\mu }}_{i\left(a\right)}^H$ et $\overline{\text{BRA}}=\text{39,6}\%$ pour ${\widehat{\mu }}_{i\left(a\right)}^{\text{YR}}.$

4.3 Sélection de la variable d’augmentation

À la présente section, nous illustrons la sélection de la variable d’augmentation en générant des données pour les $N$ unités de la population au moyen du modèle (4.1), puis en sélectionnant un échantillon dans la population de données selon la méthode de Rao-Sampford en utilisant les mesures de taille (4.2). En posant que $u_{ij}=v_i+e_{ij},$ nous avons ajusté le modèle $y_{ij}={\beta }_0+{\beta }_1{x}_{ij}+u_{ij}$ aux données d’échantillon par la méthode des moindres carrés ordinaires (MCO) et obtenu les résidus ${\tilde{u}}_{ij}=y_{ij}-{\tilde{\beta }}_0-{\tilde{\beta }}_1{x}_{ij},$ où ${\tilde{\beta }}_0$ et ${\tilde{\beta }}_1$ sont les estimateurs par les MCO de ${\beta }_0$ et ${\beta }_1,$ respectivement.

La figure 4.1 donne les graphiques des résidus de $\left({\tilde{u}}_{ij},p_{j|i}\right),\left({\tilde{u}}_{ij},\log p_{j|i}\right),\left({\tilde{u}}_{ij},n_i{w}_{j|i}\right)$ et $\left({\tilde{u}}_{ij},w_{j|i}\right).$ Les quatre graphiques indiquent clairement que l’échantillonnage est informatif. Les relations linéaires entre $u_{ij}$ et les deux choix $p_{j|i}$ et $\log p_{j|i}$ donnent à penser que n’importe lequel de ces choix devrait donner de bons résultats. Le choix $w_{j|i}$ indique une certaine non-linéarité et une plus grande dispersion du diagramme des résidus, et ce choix est, parmi les quatre, celui qui a produit la $\overline{\text{REQM}}$ la plus grande, comme le montre le tableau 4.1. Le choix $n_i{w}_{j|i}$ révèle aussi une certaine non-linéarité, mais une dispersion moins importante du graphique des résidus.

Nous avons également ajusté le modèle augmenté (1.4) avec $g\left(p_{j|i}\right)=p_{j|i}$ et calculé les résidus par les MCO ${\tilde{u}}_{0ij}=y_{ij}-{\tilde{\beta }}_{00}-{\tilde{\beta }}_{01}{x}_{ij}-{\tilde{\delta }}_0{p}_{j|i}.$ Tous les résidus ${\tilde{u}}_{0ij}$ sont inférieurs à 2,0 en valeur absolue, ce qui laisse entendre que le modèle augmenté est adéquat.

4.4 Résultats sous les mesures de taille d’Asparouhov

Le tableau 4.2 donne les résultats des simulations pour le $\overline{\text{BA}}$ sous les mesures de taille (4.3) et (4.4) d’Asparouhov. Il montre, comme le tableau 4.1 pour les mesures de taille de Pfeffermann et Sverchkov, que le $\overline{\text{BA}}$ de l’EBLUP est grand (0,437 pour la mesure de taille invariante (I) et 0,440 pour la mesure de taille non invariante (NI)) quand la variable d’augmentation, $g_{ij},$ n’est pas incluse dans le modèle et que l’échantillonnage est très informatif $\left(\alpha =1\right).$ De plus, le $\overline{\text{BA}}$ diminue à mesure que $\alpha$ augmente. Par ailleurs, sous le même modèle, le $\overline{\text{BA}}$ associé au pseudo-EBLUP est beaucoup plus faible : 0,048 pour I et 0,047 pour NI quand $\alpha =1,$ et le $\overline{\text{BA}}$ diminue quand $\alpha$ augmente. L’estimateur de Pfeffermann et Sverchkov sous le même modèle présente aussi un $\overline{\text{BA}}$ plus faible (environ 0,01), quel que soit le choix de la valeur de $\alpha .$ L’inclusion de $p_{j|i}$ ou $n_i{w}_{j|i}$ ou $\log p_{j|i}$ comme variable d’augmentation dans le modèle donne aussi lieu à un petit $\overline{\text{BA}}$ pour l’EBLUP (0,02 ou moins), quelle que soit la valeur de $\alpha .$ Par ailleurs, le choix $w_{j|i}$ comme variable d’augmentation entraîne un plus grand $\overline{\text{BA}}$ (0,14 pour $\alpha =1$ et $2),$ sauf en cas d’échantillonnage non informatif $\left(\alpha =\infty \right).$ Ces résultats médiocres pour le choix $w_{j|i}$ sont probablement dus au fait que $w_{j|i}={\left(n_i{p}_{j|i}\right)}^{-1}$ dépend des tailles d’échantillon de domaine, $n_i,$ quand celles-ci ne sont pas égales, contrairement aux autres choix de $g_{ij}.$ Le pseudo-EBLUP donne des résultats comparables à l’EBLUP sous le modèle augmenté en ce qui concerne le $\overline{\text{BA}}.$

Le tableau 4.3 présente les résultats des simulations concernant la racine carrée moyenne de l’erreur quadratique moyenne $\left(\overline{\text{REQM}}\right)$ lorsque l’on utilise les mesures de taille (4.3) et (4.4) d’Asparouhov. Les résultats montrent que l’EBLUP, fondé sur le modèle (1.4) sans la variable d’augmentation $g_{ij},$ est celui dont la $\overline{\text{REQM}}$ est la plus grande (0,596 pour I et 0,619 pour NI) quand l’échantillonnage est très informatif $\left(\alpha =1\right).$ La $\overline{\text{REQM}}$ diminue progressivement jusqu’à environ 0,42 au fur et à mesure que l’échantillonnage devient non informatif $\left(\alpha =\infty \right).$ Par ailleurs, la $\overline{\text{REQM}}$ du pseudo-EBLUP (sans le terme $g_{ij}$ dans le modèle) et de l’estimateur PS ne dépend pas de $\alpha ,$ et est considérablement réduite : la $\overline{\text{REQM}}$ du pseudo-EBLUP est de l’ordre de 0,44 et la $\overline{\text{REQM}}$ de l’estimateur PS est un peu plus petite, de l’ordre de 0,42. L’augmentation de la $\overline{\text{REQM}}$ des estimateurs pseudo-EBLUP et PS par rapport à l’estimateur EBLUP sous échantillonnage non informatif $\left(\alpha =\infty \right)$ est également faible. Par ailleurs, l’utilisation de l’EBLUP et du pseudo-EBLUP sous le modèle augmenté donne lieu à une réduction importante de l’EQM quand l’échantillonnage est très informatif $\left(\alpha =1\right),$ particulièrement pour les choix $p_{j|i}$ et $\log p_{j|i}:\overline{\text{REQM}}$ inférieure à 0,15. Le choix $w_{j|i}$ donne une plus grande $\overline{\text{REQM}}$ (autour de 0,29) quand $\alpha =1,$ mais elle demeure néanmoins nettement plus petite que la $\overline{\text{REQM}}$ pour le pseudo-EBLUP sans le terme $g_{ij}$ et l’estimateur PS. À mesure que $\alpha$ augmente, la $\overline{\text{REQM}}$ devient à peu près la même pour les estimateurs EBLUP (sous le modèle augmenté), pseudo-EBLUP et PS.

Le tableau 4.4 donne les résultats des simulations concernant le biais relatif absolu moyen $\left(\overline{\text{BRA}}\right)$ des estimateurs de l’EQM sous les mesures de taille (4.3) et (4.4) d’Asparouhov. Il montre que le $\overline{\text{BRA}}$ de l’estimateur de l’EQM de l’EBLUP, basé sur le modèle sans la variable d’augmentation $g_{ij},$ est très grand quand l’échantillonnage est très informatif $\left(\alpha =1\right):$ 52,8 % pour I et 59,1 % pour NI. Le $\overline{\text{BRA}}$ diminue progressivement jusqu’à environ 5 % sous échantillonnage non informatif $\left(\alpha =\infty \right).$ L’utilisation de $\log p_{j|i}$ comme variable d’augmentation donne lieu à une grande réduction du $\overline{\text{BRA}}$ $\left(<9\%\right)$ et les choix $p_{j|i}$ et $n_i{w}_{j|i}$ donnent aussi de bons résultats en ce qui concerne le $\overline{\text{BRA}},$ sauf dans le cas de NI et $\alpha =1$ où le BRA vaut 18,5 % et 12,9 %, respectivement. De nouveau, $w_{j|i}$ n’est pas un bon choix parce qu’il donne un $\overline{\text{BRA}}$ aussi grand que 40 % quand $\alpha =1.$ L’estimateur de l’EQM associé au pseudo-EBLUP (sans $g_{ij})$ donne aussi de bons résultats, sauf pour NI et $\alpha =1,$ qui mènent à un $\overline{\text{BRA}}$ de 19,5 %. L’utilisation de $\log p_{j|i}$ comme variable auxiliaire produit un $\overline{\text{BRA}}$ inférieur à 8 % pour l’estimateur de l’EQM associé au pseudo-EBLUP. Nous n’avons pas inclus l’estimateur bootstrap de l’EQM de Pfeffermann et Sverchkov dans notre étude.

Dans l’ensemble, notre étude en simulation indique que l’utilisation de modèles augmentés sous échantillonnage informatif produit des estimateurs EBLUP qui donnent de bons résultats en ce qui concerne le $\overline{\text{BA}}$ et la $\overline{\text{REQM}}$ des estimateurs, et le $\overline{\text{BRA}}$ des estimateurs de l’EQM, à condition que la variable d’augmentation soit choisie convenablement. Les estimateurs corrigés du biais de Pfeffermann et Sverchkov donnent aussi de bons résultats, quoiqu’ils produisent une plus grande $\overline{\text{REQM}}$ sous les mesures de taille (4.2) de Pfeffermann et Sverchkov. Les estimateurs pseudo-EBLUP (sans la variable d’augmentation) sont également bons et une amélioration supplémentaire peut être obtenue sous les modèles augmentés.

• Précédent
• Suivant