A comparison between nonparametric estimators for finite population distribution functions 5. Simulation studyA comparison between nonparametric estimators for finite population distribution functions 5. Simulation study

In this section we analyze some simulation results. Our goal is to compare efficiency with respect to the sample design of the distribution function estimators introduced in Section 2 and of the variance estimators of Section 4. The simulation results refer to simple random without replacement sampling and to Poisson sampling with unequal inclusion probabilities. As a benchmark, we included also the Horvitz-Thompson distribution function estimator

${\hat{F}}_{π} (t) := \frac{1}{N} \sum_{j \in s} π_{j}^{- 1} I (y_{j} \leq t)$

and the corresponding variance estimator

$\tilde{V} ({\hat{F}}_{π} (t)) := \frac{1}{N^{2}} \sum_{i, j \in s} \frac{π_{i, j} - π_{i} π_{j}}{π_{i, j} π_{i} π_{j}} I (y_{i} \leq t) I (y_{j} \leq t)$

in the simulation study.

We considered both artificial and real populations. The former were obtained by generating $N = 1,000$ values $x_{i}$ from i.i.d. uniform random variables with support on the interval $(0,1)$ and by combining them with three types of regression function $m (x)$ and two types of error components $ε_{i} .$ The regression functions are (i) $m (x) =0$ (flat), (ii) $m (x) =10 x$ (linear) and (iii) $m (x) =10 x^{1 / 4}$ (concave), while the error components $ε_{i}$ are either independent realizations from a unique Student $t$ distribution with $ν =5$ d.o.f., or independent realizations from $N$ different shifted noncentral Student $t$ distributions with $ν =5$ d.o.f. and with noncentrality parameters given by $μ =15 x_{i} .$ The shifts applied to the error components in the latter case make sure that the means of the noncentral Student $t$ distributions from which they were generated are zero. The artificial populations are shown in Figure 5.1 to 5.3. As for the real populations, we took the $M U 284$ Population of Sweden Municipalities of Särndal et al. 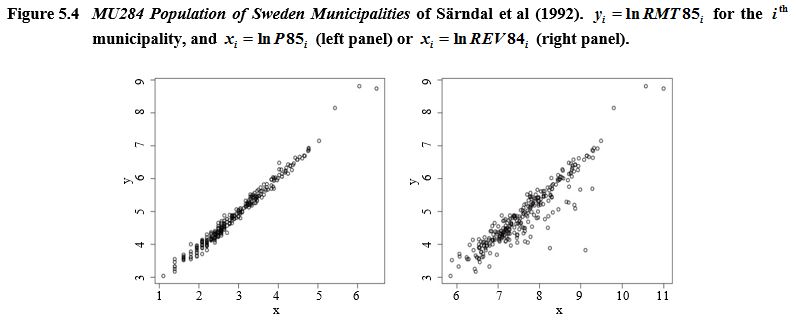(1992) (population size $N =284)$ and considered the natural logarithm of $R M T 85 =$ Revenues from the 1985 municipal taxation (in millions of kronor) as study variable $Y,$ and the natural logarithm of either $P 85 = 1985$ population (in thousands) or $R E V 84 =$ Real estate values according to 1984 assessment (in millions of kronor) as auxiliary variable $X .$ The real populations are shown in Figure 5.4.

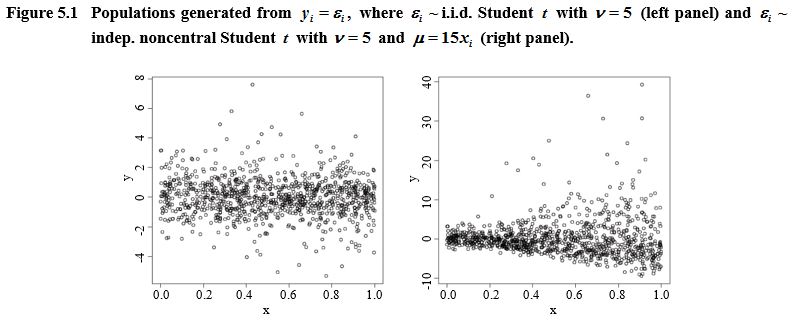
Figure 5.1 of article 14541

Description of Figure 5.1

Figure made of two scatter plots $(y$ versus $x),$ each one illustrating an artificial population. The first graph is the population generated from $y_{i} = ε_{i},$ where $ε_{i} \sim$ i.i.d. Student $t$ with $ν = 5.$ The y-axis goes from -4 to 8 and the x-axis goes from 0.0 to 1.0. The scatter plot is centered around $y = 0.$ The second graph is the population generated from $y_{i} = ε_{i}$ and $ε_{i} \sim$ indep. noncentral Student $t$ with $ν = 5$ and $μ = 15 x_{i} .$ The y-axis goes from -10 to 40 and the x-axis goes from 0.0 to 1.0. The scatter plot is concentrated around $y = 0$ for small values of $x .$ The variation increases when $x$ increases.

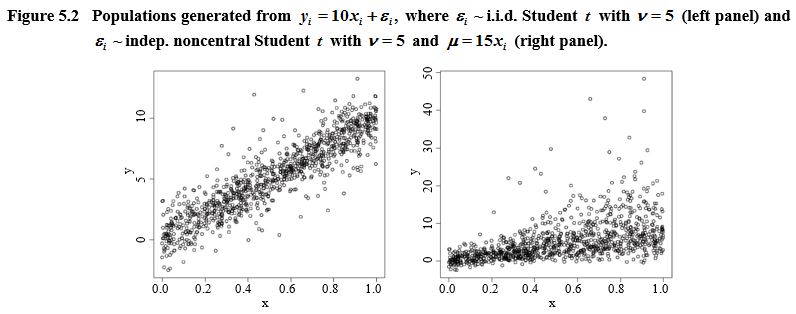
Figure 5.2 of article 14541

Description of Figure 5.2

Figure made of two scatter plots $(y$ versus $x),$ each one illustrating an artificial population. The first graph is the population generated from $y_{i} = 10 x_{i} + ε_{i},$ where $ε_{i} \sim$ i.i.d. Student $t$ with $ν = 5.$ The y-axis goes from 0 to 10 and the x-axis goes from 0.0 to 1.0. The scatter plot is showing an increasing linear relationship between $x$ and $y .$ The second graph is the population generated from $y_{i} = ε_{i}$ and $ε_{i} \sim$ indep. noncentral Student $t$ with $ν = 5$ and $μ = 15 x_{i} .$ The y-axis goes from 0 to 50 and the x-axis goes from 0.0 to 1.0. The scatter plot is showing an increasing linear relationship between $x$ and $y .$ The variation increases when x increases.

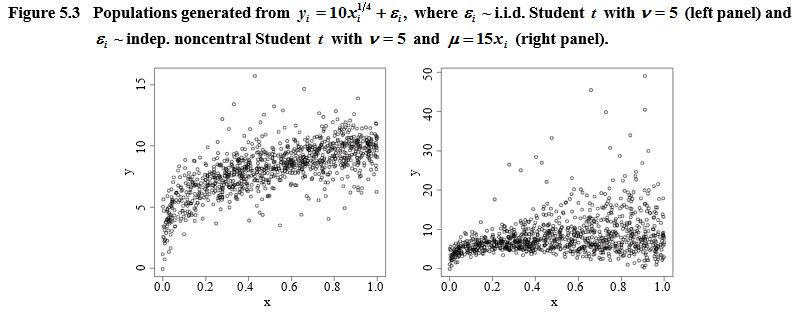
Figure 5.3 of article 14541

Description of Figure 5.3

Figure made of two scatter plots $(y$ versus $x),$ each one illustrating an artificial population. The first graph is the population generated from $y_{i} = 10 x_{i}^{1 / 4} + ε_{i},$ where $ε_{i} \sim$ i.i.d. Student $t$ with $ν = 5.$ The y-axis goes from 0 to 15 and the x-axis goes from 0.0 to 1.0. The scatter plot is showing an increasing concave relationship between $x$ and $y .$ The second graph is the population generated from $y_{i} = ε_{i}$ and $ε_{i} \sim$ indep. noncentral Student $t$ with $ν = 5$ and $μ = 15 x_{i} .$ The y-axis goes from 0 to 50 and the x-axis goes from 0.0 to 1.0. The scatter plot is showing an increasing concave relationship between $x$ and $y .$ The variation increases when $x$ increases.

Figure 5.4 of article 14541

Description of Figure 5.4

Figure made of two scatter plots $(y$ versus $x),$ each one illustrating a real population, $M U 284$ Population of Sweden Municipalities of Särndal et al (1992). On the first graph, $y_{i} = \ln R M T 85_{i}$ for the $i^{th}$ municipality and $x_{i} = \ln P 85_{i} .$ The y-axis goes from 3 to 9 and the x-axis goes from 1 to 6. The scatter plot is showing an increasing linear relationship between $x$ and $y .$ On the second graph, $y_{i} = \ln R M T 85_{i}$ for the $i^{th}$ municipality and $x_{i} = \ln R E V 84_{i} .$ The y-axis goes from 3 to 9 and the x-axis goes from 6 to 11. The scatter plot is showing a more variable increasing linear relationship between $x$ and $y .$

From each population we selected independently $B = 1,000$ samples. When sampling from the artificial populations we set the sample size equal to $n =100$ in case of simple random without replacement sampling and, in case of Poisson sampling, we set the expected sample size equal to $n^{*} =100$ and made the sample inclusion probabilities proportional to the standard deviations of the shifted noncentral Student $t$ distributions of above. When sampling from the real populations, we set the sample size equal to $n =30$ in case of simple random without replacement sampling. In case of Poisson sampling, we set the expected sample size equal to $n^{*} =30$ and made the sample inclusion probabilities proportional to the absolute values of the residuals from the linear least squares regressions of the population $y_{i}$ values on the population $x_{i}$ values.

As for the definition of the nonparametric estimators, we used the Epanechnikov kernel function $K (u) :=0.75 (1 - u^{2})$ with $λ =0.15$ or $λ =0.3$ for the samples taken from the artificial populations, and the Gaussian kernel function $K (u) := 1 / \sqrt{2 π} e^{- (1 / 2) u^{2}}$ with $λ =1$ or $λ =2$ for the samples taken from the real populations. In the tables with the simulation results the nonparametric estimators corresponding to the small and large bandwidth values are identified with an $s$ (small) or an $l$ (large) in the subscript. We resorted to the Gaussian kernel function for the samples taken from the real populations to avoid singularity problems that occur in case of holes in the sampled set of $x_{i} -$ values. Such holes are much more likely to occur with the real populations than with the artificial ones, because the distributions of the auxiliary variables are asymmetric in the former. In fact, in the artificial populations the nonparametric estimators were well-defined for all the $B = 1,000$ samples selected according to the simple random without replacement sampling design. For the Poisson sampling design, on the other hand, 47 among the $B = 1,000$ simulated samples were such that the nonparametric estimators with the small bandwidth value could not be computed and just one of these samples was such that the nonparametric estimators with the large bandwidth value were undefined. The simulation results referring to the nonparametric estimators in Tables 5.2 and 5.5 account only for the samples where they were well-defined and thus they are based on a little less than $B = 1,000$ realizations.

Tables 5.1 to 5.4 report the simulated bias (BIAS) and the simulated root mean square error (RMSE) for each distribution function estimator at different levels of $t$ at which $F_{N} (t)$ has been estimated: based, for example, on the values ${\tilde{F}}_{b} (t),$ $b =1,2, \dots, B,$ taken on by the estimator $\tilde{F} (t),$

$BIAS := \frac{1}{B} \sum_{b =1}^{B} ({\tilde{F}}_{b} (t) - F_{N} (t)) \times 10,000$

and

$RMSE := \sqrt{\frac{1}{B} \sum_{b =1}^{B} {({\tilde{F}}_{b} (t) - F_{N} (t))}^{2}} \times 10,000 .$

The RMSE’s show that the estimators based on the modified fitted values are usually more efficient. In sampling from the real populations the gain in RMSE is sometimes quite large. As expected, the model-based estimators tend to be more efficient than the generalized difference estimators in case of simple random without replacement sampling when both types of estimator are approximately unbiased. Under the Poisson sampling scheme the BIAS of the model-based estimators increases, but nonetheless they remain competitive. More variability in the sample inclusion probabilities would certainly change this outcome, because it would increase the BIAS of the model-based estimators. The simulation results should therefore not be seen to be in contrast with Johnson, Breidt and Opsomer (2008) who argue in favor of generalized difference estimators (called model-assisted estimators in their paper) as “a good overall choice for distribution function estimators”.

Table 5.1
Artificial populations (population size $N = 1,000) .$ BIAS and RMSE of distribution function estimators under simple random without replacement sampling. Sample size $n = 100$
Table summary
This table displays the results of Artificial populations (population size XXXX BIAS and RMSE of distribution function estimators under simple random without replacement sampling. Sample size XXXX XXXX , XXXX, BIAS , RMSE and RMSE, calculated using XXXX with XXXX i.i.d. central Student XXXX with XXXX, XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX, XXXX with XXXX i.i.d. Student XXXX with XXXX, XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX, XXXX with XXXX i.i.d. Student XXXX with XXXX and XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX units of measure (appearing as column headers).
	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ i.i.d. central Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	6	216	-3	433	31	512	23	434	12	207
${\hat{F}}_{l} (t)$	15	219	10	430	0	502	-10	429	3	213
${\hat{F}}_{s}^{*} (t)$	6	209	-30	411	22	484	22	414	3	200
${\hat{F}}_{l}^{*} (t)$	15	214	-9	409	10	477	1	407	-10	207
${\tilde{F}}_{s} (t)$	6	213	8	425	24	504	-4	430	8	207
${\tilde{F}}_{l} (t)$	6	210	10	417	22	494	-8	422	6	206
${\tilde{F}}_{s}^{*} (t)$	8	213	9	426	25	503	-5	432	5	206
${\tilde{F}}_{l}^{*} (t)$	7	210	10	417	23	494	-6	424	4	206
${\tilde{F}}_{π} (t)$	7	208	11	411	19	489	-5	417	6	200
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	26	225	33	376	8	477	26	419	33	209
${\hat{F}}_{l} (t)$	52	236	23	374	-5	475	38	421	29	213
${\hat{F}}_{s}^{*} (t)$	20	195	-29	351	-89	471	11	407	30	202
${\hat{F}}_{l}^{*} (t)$	36	201	-11	357	-94	473	28	410	21	204
${\tilde{F}}_{s} (t)$	8	211	11	370	-7	473	4	415	16	211
${\tilde{F}}_{l} (t)$	5	208	8	367	-5	468	5	411	16	212
${\tilde{F}}_{s}^{*} (t)$	11	210	11	372	-11	475	4	416	15	210
${\tilde{F}}_{l}^{*} (t)$	7	208	11	368	-7	468	8	412	15	211
${\tilde{F}}_{π} (t)$	1	211	1	391	-6	477	8	399	18	210
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	32	201	25	275	13	250	-14	264	-36	217
${\hat{F}}_{l} (t)$	114	250	152	304	12	236	-180	312	-86	242
${\hat{F}}_{s}^{*} (t)$	-50	165	12	226	51	216	26	230	13	172
${\hat{F}}_{l}^{*} (t)$	-46	155	-14	199	69	195	23	211	17	156
${\tilde{F}}_{s} (t)$	-5	186	4	275	15	248	11	269	-2	201
${\tilde{F}}_{l} (t)$	-5	184	7	274	17	250	5	269	-2	196
${\tilde{F}}_{s}^{*} (t)$	-10	180	5	275	16	245	14	266	-1	200
${\tilde{F}}_{l}^{*} (t)$	-9	176	3	272	15	242	13	262	-1	194
${\tilde{F}}_{π} (t)$	-7	203	14	413	37	472	17	405	1	206
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	24	204	23	351	27	403	26	382	29	208
${\hat{F}}_{l} (t)$	94	242	135	372	51	392	13	380	15	212
${\hat{F}}_{s}^{*} (t)$	55	182	-9	301	-18	368	-23	359	37	202
${\hat{F}}_{l}^{*} (t)$	124	210	-31	278	-63	363	-8	356	48	200
${\tilde{F}}_{s} (t)$	-2	194	-4	349	11	401	18	377	13	208
${\tilde{F}}_{l} (t)$	-2	190	-5	345	12	398	17	374	11	209
${\tilde{F}}_{s}^{*} (t)$	0	191	-5	352	14	401	20	376	13	207
${\tilde{F}}_{l}^{*} (t)$	-1	189	-6	344	13	397	18	375	12	209
${\tilde{F}}_{π} (t)$	-4	205	-5	401	21	470	24	401	14	207
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	81	207	44	316	17	384	-2	376	23	203
${\hat{F}}_{l} (t)$	138	258	183	356	35	367	-50	374	8	208
${\hat{F}}_{s}^{*} (t)$	7	146	-14	274	16	352	-8	358	15	197
${\hat{F}}_{l}^{*} (t)$	9	144	10	246	-2	323	-18	339	24	186
${\tilde{F}}_{s} (t)$	3	175	3	319	10	383	17	374	10	203
${\tilde{F}}_{l} (t)$	0	178	5	316	11	380	17	370	8	202
${\tilde{F}}_{s}^{*} (t)$	1	167	5	320	12	383	17	374	9	203
${\tilde{F}}_{l}^{*} (t)$	-1	164	6	316	13	379	20	368	8	201
${\tilde{F}}_{π} (t)$	4	209	11	412	25	477	27	422	10	200
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	59	234	95	402	66	455	51	395	26	208
${\hat{F}}_{l} (t)$	94	259	190	441	147	467	98	400	16	212
${\hat{F}}_{s}^{*} (t)$	30	184	33	343	-123	435	-34	385	40	203
${\hat{F}}_{l}^{*} (t)$	57	201	58	331	-148	437	2	382	34	203
${\tilde{F}}_{s} (t)$	1	205	7	386	12	449	17	392	13	208
${\tilde{F}}_{l} (t)$	-1	204	0	385	9	445	20	389	11	209
${\tilde{F}}_{s}^{*} (t)$	3	201	8	389	7	449	13	392	14	207
${\tilde{F}}_{l}^{*} (t)$	0	198	6	383	9	446	19	390	13	208
${\tilde{F}}_{π} (t)$	0	205	-2	399	9	463	25	398	14	208

Table 5.2
Artificial populations (population size $N = 1,000) .$ BIAS and RMSE of distribution function estimators under Poisson sampling with sample inclusion probabilities $π_{i}$ proportional to the standard deviations of the noncentral Student $t$ distributions with $ν =5$ d.o.f. and with noncentrality parameters $μ =15 x_{i} .$ Expected sample size $n^{*} =100$
Table summary
This table displays the results of Artificial populations (population size XXXX BIAS and RMSE of distribution function estimators under Poisson sampling with sample inclusion probabilities XXXX proportional to the standard deviations of the noncentral Student XXXX distributions with XXXX d.o.f. and with noncentrality parameters XXXX Expected sample size XXXX XXXX, BIAS , RMSE and RMSE, calculated using XXXX with XXXX i.i.d. central Student XXXX with XXXX, XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX, XXXX with XXXX i.i.d. Student XXXX with XXXX, XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX, XXXX with XXXX i.i.d. Student XXXX with XXXX and XXXX with XXXX indep. noncentral Student XXXX with XXXX and XXXX units of measure (appearing as column headers).
	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE	BIAS	RMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ i.i.d. central Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	-10	252	-11	593	-22	738	-20	743	6	357
${\hat{F}}_{l} (t)$	-1	237	9	543	-15	621	-5	590	11	302
${\hat{F}}_{s}^{*} (t)$	22	244	-29	485	-3	555	9	515	-17	297
${\hat{F}}_{l}^{*} (t)$	14	238	-10	492	-5	564	14	524	-1	283
${\tilde{F}}_{s} (t)$	-6	247	0	579	-27	724	-40	736	3	349
${\tilde{F}}_{l} (t)$	-2	231	11	526	-1	598	-10	566	7	285
${\tilde{F}}_{s}^{*} (t)$	23	248	23	505	-4	562	-27	531	-20	304
${\tilde{F}}_{l}^{*} (t)$	12	240	20	504	1	573	-13	538	-6	287
${\tilde{F}}_{π} (t)$	-6	220	-7	543	-37	741	-44	929	-48	1,058
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	17	164	30	411	4	749	14	590	15	190
${\hat{F}}_{l} (t)$	47	173	19	383	-1	602	57	498	15	187
${\hat{F}}_{s}^{*} (t)$	21	175	-7	378	-89	554	-11	473	3	192
${\hat{F}}_{l}^{*} (t)$	29	152	-3	367	-99	555	27	481	3	184
${\tilde{F}}_{s} (t)$	1	159	10	406	-11	737	-5	579	-2	194
${\tilde{F}}_{l} (t)$	1	158	9	388	-5	586	14	482	-1	192
${\tilde{F}}_{s}^{*} (t)$	14	186	27	409	-3	562	-17	487	-10	200
${\tilde{F}}_{l}^{*} (t)$	3	160	22	399	-11	566	-5	482	-2	193
${\tilde{F}}_{π} (t)$	-3	162	-7	451	-31	738	-29	980	-55	1,067
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	8	461	21	561	-12	259	-18	218	-30	164
${\hat{F}}_{l} (t)$	78	429	183	451	2	248	-161	261	-79	189
${\hat{F}}_{s}^{*} (t)$	-69	306	12	340	10	267	15	199	6	143
${\hat{F}}_{l}^{*} (t)$	-59	294	4	302	56	205	15	172	17	124
${\tilde{F}}_{s} (t)$	-25	441	4	560	-10	257	9	219	5	153
${\tilde{F}}_{l} (t)$	-14	372	35	410	-10	262	4	219	5	151
${\tilde{F}}_{s}^{*} (t)$	-31	333	-2	386	-29	294	4	227	-1	161
${\tilde{F}}_{l}^{*} (t)$	-20	339	15	372	-10	259	11	215	4	151
${\tilde{F}}_{π} (t)$	-15	385	3	746	-37	917	-35	1,004	-48	1,070
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	-4	516	30	671	7	453	11	344	6	182
${\hat{F}}_{l} (t)$	63	409	129	539	61	421	9	341	1	180
${\hat{F}}_{s}^{*} (t)$	44	300	-29	433	-45	422	-47	345	12	180
${\hat{F}}_{l}^{*} (t)$	107	314	-41	420	-60	397	-22	323	31	171
${\tilde{F}}_{s} (t)$	-27	502	8	667	-8	450	0	344	-8	185
${\tilde{F}}_{l} (t)$	-10	364	16	510	11	425	-2	345	-7	182
${\tilde{F}}_{s}^{*} (t)$	-6	325	-9	479	-25	447	-14	356	-10	187
${\tilde{F}}_{l}^{*} (t)$	-7	332	-9	489	-5	426	-3	344	-6	182
${\tilde{F}}_{π} (t)$	-16	349	-2	705	-21	886	-42	1,013	-61	1,069
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
${\hat{F}}_{s} (t)$	36	497	47	629	9	418	-11	320	15	191
${\hat{F}}_{l} (t)$	56	393	186	490	43	383	-48	308	13	184
${\hat{F}}_{s}^{*} (t)$	-29	276	-19	383	-18	380	-43	335	-1	204
${\hat{F}}_{l}^{*} (t)$	-29	274	10	355	7	336	-29	290	23	179
${\tilde{F}}_{s} (t)$	-30	475	12	630	4	421	7	317	6	191
${\tilde{F}}_{l} (t)$	-42	336	31	452	11	390	8	312	8	186
${\tilde{F}}_{s}^{*} (t)$	-31	306	5	429	-18	406	-14	344	-8	210
${\tilde{F}}_{l}^{*} (t)$	-28	308	14	424	7	387	5	315	7	191
${\tilde{F}}_{π} (t)$	-15	380	10	739	-23	891	-37	993	-47	1,064
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	24	308	69	687	53	690	38	406	2	188
${\hat{F}}_{l} (t)$	47	301	131	553	139	561	91	393	-2	186
${\hat{F}}_{s}^{*} (t)$	15	237	2	435	-135	513	-59	411	12	186
${\hat{F}}_{l}^{*} (t)$	27	235	18	435	-149	506	-5	374	13	179
${\tilde{F}}_{s} (t)$	-28	274	-8	673	4	688	3	403	-10	191
${\tilde{F}}_{l} (t)$	-29	251	-12	512	17	541	7	395	-9	188
${\tilde{F}}_{s}^{*} (t)$	-3	255	-12	481	-7	536	-20	422	-12	196
${\tilde{F}}_{l}^{*} (t)$	-12	251	-16	489	2	538	-4	399	-9	189
${\tilde{F}}_{π} (t)$	-10	267	-8	608	-4	860	-38	1,009	-63	1,066

Table 5.3
Real populations (population size $N =284) .$ BIAS and RMSE of distribution function estimators under simple random without replacement sampling. Sample size $n =30$
Table summary
This table displays the results of Real populations (population size XXXX BIAS and RMSE of distribution function estimators under simple random without replacement sampling. Sample size XXXX XXXX, BIAS , RMSE , RMSE and RBIAS , calculated using MU284 population with XXXX and XXXX units of measure (appearing as column headers).
	BIAS	RMSE	BIAS	RMSE	RBIAS	RMSE	BIAS	RMSE	BIAS	RMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	MU284 population with $Y = \ln R M T 85$ and $X = \ln P 85$
${\hat{F}}_{s} (t)$	133	421	339	625	180	529	-265	490	-187	439
${\hat{F}}_{l} (t)$	52	380	67	588	45	555	-63	469	-87	370
${\hat{F}}_{s}^{*} (t)$	8	81	-154	203	90	130	62	123	6	54
${\hat{F}}_{l}^{*} (t)$	28	66	-170	212	69	112	57	109	2	50
${\tilde{F}}_{s} (t)$	-28	300	-24	497	8	483	-48	421	-38	319
${\tilde{F}}_{l} (t)$	-28	326	-96	569	-52	544	3	466	1	319
${\tilde{F}}_{s}^{*} (t)$	26	177	-11	302	0	244	1	308	-18	102
${\tilde{F}}_{l}^{*} (t)$	29	179	-10	302	-2	243	-1	308	-21	104
${\tilde{F}}_{π} (t)$	22	388	-10	771	9	864	5	731	-43	394
	MU284 population with $Y = \ln R M T 85$ and $X = \ln R E V 84$
${\hat{F}}_{s} (t)$	143	449	303	643	138	554	-217	543	-166	446
${\hat{F}}_{l} (t)$	62	395	62	611	36	582	-49	519	-71	376
${\hat{F}}_{s}^{*} (t)$	-11	204	-32	300	-101	328	42	285	31	155
${\hat{F}}_{l}^{*} (t)$	36	183	-40	288	-149	345	6	261	34	122
${\tilde{F}}_{s} (t)$	5	340	-22	548	4	557	-30	498	-23	332
${\tilde{F}}_{l} (t)$	-2	349	-78	599	-36	588	10	522	8	331
${\tilde{F}}_{s}^{*} (t)$	24	303	7	446	-6	494	2	439	-13	209
${\tilde{F}}_{l}^{*} (t)$	29	304	4	443	-6	495	-1	432	-18	192
${\tilde{F}}_{π} (t)$	34	395	1	766	16	880	9	744	-37	398

Table 5.4
Real populations (population size $N =284) .$ BIAS and RMSE of distribution function estimators under Poisson sampling with inclusion probabilities proportional to the absolute value of the residuals of the linear regression of the population $y_{i} -$ values on the population $x_{i} -$ values. Expected size $n^{*} =30$
Table summary
This table displays the results of Real populations (population size XXXX BIAS and RMSE of distribution function estimators under Poisson sampling with inclusion probabilities proportional to the absolute value of the residuals of the population XXXX values on the population XXXX values. Expected size XXXX. The information is grouped by (appearing as row headers), XXXX, BIAS , RMSE , RMSE and RBIAS , calculated using MU284 population with XXXX and XXXX units of measure (appearing as column headers).
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	BIAS	RMSE	BIAS	RMSE	RBIAS	RMSE	BIAS	RMSE	BIAS	RMSE
	MU284 population with $Y = \ln R M T 85$ and $X = \ln P 85$
${\hat{F}}_{s} (t)$	204	420	485	668	239	519	-412	626	-90	317
${\hat{F}}_{l} (t)$	180	424	417	684	319	614	-239	548	-148	348
${\hat{F}}_{s}^{*} (t)$	-41	97	-118	199	132	178	40	140	-71	104
${\hat{F}}_{l}^{*} (t)$	11	70	-147	211	63	128	-25	122	-85	106
${\tilde{F}}_{s} (t)$	24	360	30	649	0	675	-68	614	58	368
${\tilde{F}}_{l} (t)$	9	390	-63	737	-64	774	-7	682	75	414
${\tilde{F}}_{s}^{*} (t)$	16	184	-14	307	36	283	16	323	-11	103
${\tilde{F}}_{l}^{*} (t)$	25	187	-15	312	30	286	14	328	-11	112
${\tilde{F}}_{π} (t)$	40	445	73	1,983	12	2,498	-43	3,094	-49	3,341
	MU284 population with $Y = \ln R M T 85$ and $X = \ln R E V 84$
${\hat{F}}_{s} (t)$	349	660	1,185	1,373	890	1,059	458	654	-32	270
${\hat{F}}_{l} (t)$	287	601	1,003	1,236	771	989	484	695	42	263
${\hat{F}}_{s}^{*} (t)$	317	453	739	866	761	879	624	701	159	207
${\hat{F}}_{l}^{*} (t)$	364	471	720	842	718	824	572	647	96	158
${\tilde{F}}_{s} (t)$	35	488	82	818	-31	772	7	634	-8	326
${\tilde{F}}_{l} (t)$	22	500	3	878	-98	852	40	704	27	354
${\tilde{F}}_{s}^{*} (t)$	37	317	32	498	-13	513	32	412	7	157
${\tilde{F}}_{l}^{*} (t)$	51	313	30	498	-30	518	12	411	-10	149
${\tilde{F}}_{π} (t)$	32	671	19	1,658	-172	2,354	-173	2,787	-191	2,935

Consider finally the simulation results referring to the variance estimators of Section 4. Tables 5.5 to 5.8 report the relative bias (RBIAS) and the relative root mean square error (RRMSE) for each of them. For example, based on the variance estimates ${\tilde{V}}_{b} (\tilde{F} (t)),$ $b =1,2, \dots, B,$ obtained from the estimator $\tilde{V} (\tilde{F} (t)),$

$RBIAS := \frac{1}{B} \sum_{b =1}^{B} \frac{{\tilde{V}}_{b} (\tilde{F} (t)) - V_{B} (\tilde{F} (t))}{V_{B} (\tilde{F} (t))} \times 10,000$

and

$RRMSE := \frac{\sqrt{\frac{1}{B} \sum_{b =1}^{B} {({\tilde{V}}_{b} (\tilde{F} (t)) - V_{B} (\tilde{F} (t)))}^{2}}}{V_{B} (\tilde{F} (t))} \times 10,000$

where

$V_{B} (\tilde{F} (t)) := \frac{1}{B} \sum_{b =1}^{B} {({\tilde{F}}_{b} (t) - F_{N} (t))}^{2} .$

As a benchmark, we report also the RBIAS and RRMSE of the estimator

$\tilde{V} ({\tilde{F}}_{π} (t)) := \frac{1}{N^{2}} \sum_{i, j \in s} \frac{π_{i, j} - π_{i} π_{j}}{π_{i, j} π_{i} π_{j}} I (y_{i} \leq t) I (y_{j} \leq t) .$

for the variance of the Horvitz-Thompson estimator.

Table 5.5
Artificial populations (population size $N = 1,000) .$ RBIAS and RRMSE of variance estimators under simple random without replacement sampling. Sample size $n =100$
Table summary
This table displays the results of Artificial populations (population size XXXX RBIAS and RRMSE of variance estimators under simple random without replacement sampling. Sample size XXXX. The information is grouped by (appearing as row headers), XXXX, RBIAS , RRMSE and RRMSE, calculated using XXXX with XXXX i.i.d. central Student XXXX with XXXX and XXXX with XXXX i.i.d. Student XXXX with XXXX units of measure (appearing as column headers).
	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ i.i.d. central Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1,092	32,442	-1,249	3,895	-1,714	3,077	-1,536	3,828	-824	34,601
$\tilde{V} ({\tilde{F}}_{l} (t))$	-576	31,726	-603	3,838	-1,122	3,374	-951	3,758	-441	33,055
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,091	32,579	-1,292	3,914	-1,708	3,085	-1,640	3,828	-802	34,809
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-556	31,881	-622	3,857	-1,148	3,361	-1,025	3,749	-425	33,184
$\tilde{V} ({\tilde{F}}_{π} (t))$	42	30,952	57	3,928	-592	3,776	-287	3,825	551	33,462
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1,900	29,622	50	4,707	-917	3,557	-998	3,695	-1,480	29,417
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,359	29,623	535	4,572	-395	3,881	-527	3,736	-1,277	28,267
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,832	30,119	-101	4,710	-991	3,530	-1,077	3,704	-1,398	29,927
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1,362	29,713	465	4,559	-420	3,865	-591	3,718	-1,236	28,489
$\tilde{V} ({\tilde{F}}_{π} (t))$	-351	29,132	1,096	4,215	-78	4,074	574	4,067	-638	29,507
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2,170	11,624	-1,027	2,480	-816	3,274	-1,424	2,583	-1,946	8,681
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,534	11,605	-529	2,632	-148	2,975	-859	2,590	-1,151	9,015
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,765	12,107	-1,108	2,529	-714	3,366	-1,318	2,660	-1,905	8,658
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1,062	11,948	-671	2,735	-212	3,291	-762	2,785	-1,048	8,590
$\tilde{V} ({\tilde{F}}_{π} (t))$	254	31,545	-52	3,726	136	4,152	267	3,992	35	30,264
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1,642	25,809	-855	3,541	-1,076	3,038	-1,081	3,030	-1,361	21,157
$\tilde{V} ({\tilde{F}}_{l} (t))$	-950	25,692	-323	3,509	-597	3,312	-617	3,164	-1,124	20,231
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,385	26,406	-997	3,505	-1,089	3,045	-1,096	3,033	-1,310	21,393
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-832	26,212	-292	3,556	-614	3,317	-716	3,154	-1,135	20,286
$\tilde{V} ({\tilde{F}}_{π} (t))$	105	29,621	507	3,857	209	4,244	425	3,910	-337	29,082
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2,465	30,612	-1,121	4,594	-1,512	3,183	-1,958	3,076	-863	19,720
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,780	28,103	-663	4,420	-1,092	3,319	-1,491	3,140	-439	18,985
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-2,052	33,980	-1,150	4,619	-1,537	3,217	-1,948	3,127	-954	19,637
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1,194	33,573	-691	4,472	-1,124	3,368	-1,438	3,228	-357	19,245
$\tilde{V} ({\tilde{F}}_{π} (t))$	-81	30,001	9	3,756	-110	3,996	-598	3,661	440	32,455
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1,873	29,437	-758	3,759	-621	3,476	-709	3,599	-1,298	27,679
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,267	28,511	-284	3,661	-131	3,758	-321	3,552	-1,075	26,790
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,710	30,670	-928	3,741	-628	3,510	-777	3,603	-1,245	27,972
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-939	30,486	-270	3,764	-171	3,803	-375	3,581	-1,014	26,926
$\tilde{V} ({\tilde{F}}_{π} (t))$	178	29,640	599	3,816	533	4,324	590	3,874	-404	28,917

Table 5.6
Artificial populations (population size $N = 1,000) .$ RBIAS and RRMSE of variance estimators under Poisson sampling with sample inclusion probabilities $π_{i}$ proportional to standard deviation of noncentral Student $t$ distribution with $ν =5$ d.f. and with noncentrality parameter $μ =15 x_{i} .$ Expected sample size $n^{*} =100$
Table summary
This table displays the results of Artificial populations (population size XXXX RBIAS and RRMSE of variance estimators under Poisson sampling with sample inclusion probabilities XXXX proportional to standard deviation of noncentral Student XXXX distribution with XXXX d.f. and with noncentrality parameter XXXX Expected sample size XXXX XXXX, RBIAS , RRMSE and RRMSE, calculated using XXXX with XXXX i.i.d. central Student XXXX with XXXX units of measure (appearing as column headers).
	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ i.i.d. central Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-3,306	65,777	-4,248	8,032	-5,093	4,242	-6,258	4,844	-5,652	32,037
$\tilde{V} ({\tilde{F}}_{l} (t))$	-2,048	47,035	-2,656	4,705	-2,434	3,116	-3,310	3,939	-3,092	29,380
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3,362	36,855	-2,488	4,409	-1,910	3,147	-2,869	3,910	-4,329	23,247
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-2,696	39,509	-2,076	4,450	-1,768	3,163	-2,648	3,811	-3,244	26,343
$\tilde{V} ({\tilde{F}}_{π} (t))$	113	129,637	259	15,120	618	6,327	193	5,429	273	6,097
	$y_{i} = ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-740	125,975	-2,522	14,864	-5,466	3,658	-4,896	6,691	-1,551	83,262
$\tilde{V} ({\tilde{F}}_{l} (t))$	-391	83,047	-1,503	8,946	-2,428	4,099	-2,228	5,526	-1,154	54,680
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3,260	58,072	-2,649	7,661	-2,260	3,936	-2,795	5,011	-2,116	48,739
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-716	77,935	-2,000	7,979	-1,934	4,235	-2,279	5,243	-1,243	52,531
$\tilde{V} ({\tilde{F}}_{π} (t))$	666	251,134	-564	26,553	-87	7,344	-2	6,029	407	6,610
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-6,801	7,898	-6,470	4,281	-1,059	22,596	-398	32,401	-1,650	72,632
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4,978	5,826	-2,898	4,473	-603	9,530	206	15,226	-1,157	40,466
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4,520	6,691	-2,710	4,213	-3,245	6,723	-1,156	12,681	-2,458	32,907
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-4,226	6,206	-1,674	5,062	-978	7,874	55	12,781	-1,283	33,737
$\tilde{V} ({\tilde{F}}_{π} (t))$	-707	47,550	118	7,214	609	4,409	743	4,628	435	4,800
	$y_{i} =10 x_{i} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-7,398	8,847	-6,235	3,667	-2,493	8,171	-1,051	16,299	-1,440	71,943
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4,548	9,463	-3,136	3,282	-1,187	4,246	-832	7,638	-982	45,182
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3,902	11,727	-2,808	3,409	-2,411	3,501	-1,721	6,737	-1,671	41,389
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-3,598	10,771	-2,610	3,462	-1,284	3,988	-852	7,008	-972	43,017
$\tilde{V} ({\tilde{F}}_{π} (t))$	146	57,044	-42	8,708	520	4,784	214	4,686	390	5,085
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ i.i.d. Student $t$ with $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-7,731	8,568	-6,597	3,484	-2,442	7,775	-903	16,067	-1,967	56,480
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4,611	9,378	-2,990	3,252	-874	4,119	-347	7,420	-1,310	35,051
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4,747	11,909	-2,679	3,298	-1,896	3,272	-2,248	5,747	-3,382	27,222
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-4,223	10,380	-2,100	3,494	-788	3,731	-550	5,975	-1,795	29,856
$\tilde{V} ({\tilde{F}}_{π} (t))$	-428	47,038	-206	7,350	641	4,504	738	4,708	487	4,943
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ with $ε_{i} \sim$ indep. noncentral Student $t$ with $ν =5$ and $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-4,936	40,696	-6,111	4,579	-5,549	4,035	-1,864	14,381	-1,509	84,892
$\tilde{V} ({\tilde{F}}_{l} (t))$	-3,004	29,404	-2,764	3,962	-2,436	3,606	-1,234	7,357	-1,103	53,875
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4,328	27,704	-2,516	4,235	-2,671	3,332	-2,586	5,955	-1,939	47,601
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-3,454	28,267	-2,263	4,160	-2,329	3,574	-1,433	6,682	-1,171	50,985
$\tilde{V} ({\tilde{F}}_{π} (t))$	152	98,607	663	12,879	15	5,376	20	5,080	429	5,619

Table 5.7
Real populations (population size $N =284) .$ RBIAS and RRMSE of variance estimators under simple random without replacement sampling. Sample size $n =30$
Table summary
This table displays the results of Real populations (population size XXXX RBIAS and RRMSE of variance estimators under simple random without replacement sampling. Sample size XXXX XXXX, RBIAS , RRMSE and RRMSE, calculated using MU284 population with XXXX and XXXX and MU284 population with XXXX and XXXX units of measure (appearing as column headers).
	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	MU284 population with $Y = \ln R M T 85$ and $X = \ln P 85$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2,853	16,809	-1,700	3,037	-1,554	2,984	-1,100	4,633	-5,503	16,257
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,110	16,374	-1,827	2,760	-1,683	2,847	-927	4,387	-3,016	18,685
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,043	19,081	-91	7,728	-448	9,120	-484	7,715	-1,877	65,298
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-424	18,971	104	7,819	-382	9,110	-301	7,799	-1,058	62,968
$\tilde{V} ({\tilde{F}}_{π} (t))$	-186	29,720	-603	3,901	31	3,971	500	4,383	-74	28,418
	MU284 population with $Y = \ln R M T 85$ and $X = \ln R E V 84$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2,283	16,303	-1,450	3,538	-945	3,526	-1,071	4,300	-4,832	19,401
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1,095	16,755	-1,427	3,181	-938	3,390	-780	4,051	-2,753	20,551
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1,737	14,642	-298	5,648	-546	5,282	-736	5,679	-3,564	38,344
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1,174	14,111	-27	5,856	-422	5,452	-228	5,974	-1,433	43,923
$\tilde{V} ({\tilde{F}}_{π} (t))$	-307	28,421	-460	3,963	-344	3,850	112	4,235	-401	27,987

Table 5.8
Real populations (population size $N =284) .$ RBIAS and RRMSE of variance estimators under Poisson sampling with inclusion probabilities proportional to the absolute value of the residuals of the linear regression of the population $y_{i} -$ values on the population $x_{i} -$ values. Expected size $n^{*} =30$
Table summary
This table displays the results of Real populations (population size XXXX RBIAS and RRMSE of variance estimators under Poisson sampling with inclusion probabilities proportional to the absolute value of the residuals of the linear regression of the population XXXX values on the population XXXX values. Expected size XXXX XXXX, RBIAS , RRMSE and RRMSE, calculated using MU284 population with XXXX and XXXX and MU284 population with XXXX and XXXX units of measure (appearing as column headers).
	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE	RBIAS	RRMSE
	$t = F_{N}^{- 1} (0.05)$		$t = F_{N}^{- 1} (0.25)$		$t = F_{N}^{- 1} (0.50)$		$t = F_{N}^{- 1} (0.75)$		$t = F_{N}^{- 1} (0.95)$
	MU284 population with $Y = \ln R M T 85$ and $X = \ln P 85$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-3,502	26,342	-1,841	14,037	-2,691	12,087	-3,415	9,674	-5,932	26,823
$\tilde{V} ({\tilde{F}}_{l} (t))$	-2,159	27,610	-1,782	14,010	-2,840	12,002	-3,186	10,177	-4,455	26,802
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-434	22,455	515	15,503	-506	31,296	-1,460	23,496	-2,649	78,527
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-80	22,921	677	15,575	-280	33,294	-1,283	26,612	-1,597	72,166
$\tilde{V} ({\tilde{F}}_{π} (t))$	-294	361,991	522	75,891	43	48,764	-241	36,354	90	32,354
	MU284 population with $Y = \ln R M T 85$ and $X = \ln R E V 84$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-5,220	18,699	-3,667	8,749	-3,222	7,537	-3,018	9,279	-4,955	44,597
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4,254	20,765	-3,100	9,180	-3,435	7,231	-3,196	8,540	-3,461	43,206
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-2,938	18,922	-1,110	11,828	-1,265	8,726	-1,040	10,963	-3,682	89,262
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1,938	19,997	-699	12,641	-1,003	9,305	-599	11,545	-1,558	98,798
$\tilde{V} ({\tilde{F}}_{π} (t))$	-143	128,401	493	33,934	-255	18,473	-91	17,904	327	16,463

As can be seen from the simulation results, the variance estimators suffer from large variability. This problem is shared by the variance estimator for the Horvitz-Thompson estimator, which occasionally exhibits extremely large RRMSE’s. It is further interesting to note that while the RBIAS of the variance estimators for the generalized difference estimators is almost always negative and at times rather large in absolute value, the RBIAS of the variance estimator for the Horvitz-Thompson estimator is in most of the considered cases positive.

Acknowledgements

This research was partially supported by the FAR 2014-ATE-0200 grant from University of Milano-Bicocca.

Appendix

Let $β$ denote a sequence of real numbers. Throughout this appendix we shall indicate by $O_{i_{1}, i_{2}, \dots, i_{k}} (β)$ rest terms that may depend on $x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}$ and that are of the same order as the sequence $β$ uniformly for $i_{1}, i_{2}, \dots, i_{k} \in U .$ Formally, $R (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}) = O_{i_{1}, i_{2}, \dots, i_{k}} (β)$ if

$\sup_{i_{1}, i_{2}, \dots, i_{k} \in U} | R (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}) | = O (β) .$

Moreover, to simplify the notation, we shall write $m_{i}$ in place of $m (x_{i})$ and $σ_{i}^{2}$ in place of $σ^{2} (x_{i}) .$

Bias of the model-based Kuo estimator

$\begin{array}{l} E (\hat{F} (t) - F_{N} (t)) & = E (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})]) \\ = \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{j} | x_{j}) - G (t - m_{i} | x_{i})] \\ = \frac{1}{2 N} \sum_{i \notin s} [G^{(2,0)} (t - m_{i} | x_{i}) {(m_{i'})}^{2} - G^{(1,0)} (t - m_{i} | x_{i}) m_{i''} \\ - 2 G^{(1,1)} (t - m_{i} | x_{i}) m_{i'} + G^{(0, 2)} (t - m_{i} | x_{i})] \sum_{j \in s} w_{i, j} {(x_{j} - x_{i})}^{2} + o (λ^{2}) \\ = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{2 μ_{0}} \int_{a}^{b} [G^{(2,0)} (t - m (x) | x) {(m^{'} (x))}^{2} - G^{(1,0)} (t - m (x) | x) m^{''} (x) \\ - 2 G^{(1,1)} (t - m (x) | x) m^{'} (x) + G^{(0, 2)} (t - m (x) | x)] h_{\bar{s}} (x) d x + o (λ^{2}) . \end{array}$

Bias of the generalized difference Kuo estimator

Write

$\begin{array}{l} \tilde{F} (t) - F_{N} (t) & = \frac{1}{N} {\sum_{i \notin s} \sum_{j \in s} {\tilde{w}}_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})] \\ + \sum_{i \in s} (1 - \frac{1}{π_{i}}) \sum_{j \in s} {\tilde{w}}_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})]} . \end{array}$

Similar steps as those seen for $\hat{F} (t)$ show that

$\begin{array}{l} E (\tilde{F} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{2 μ_{0}} \int_{a}^{b} [G^{(2,0)} (t - m (x) | x) {(m^{'} (x))}^{2} - G^{(1,0)} (t - m (x) | x) m^{''} (x) \\ - 2 G^{(1,1)} (t - m (x) | x) m^{'} (x) + G^{(0, 2)} (t - m (x) | x)] h (x) d x + o (λ^{2}), \end{array}$

where

$h (x) := h_{\bar{s}} (x) + (1 - π^{- 1} (x)) h_{s} (x) .$

Variance of the model-based Kuo estimator

$\begin{array}{l} var (\hat{F} (t) - F_{N} (t)) & = var (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} I (ε_{j} \leq t - m_{j}) - \frac{1}{N} \sum_{i \notin s} I (y_{i} \leq t)) \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] \\ + \frac{1}{N^{2}} \sum_{i \notin s} [G (t - m_{i} | x_{i}) - G^{2} (t - m_{i} | x_{i})] \\ = A_{1} + A_{2}, \end{array}$

where

$\begin{array}{l} A_{1} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {(\sum_{i \notin s} w_{i, j})}^{2} \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α) \end{array}$

and

$\begin{array}{l} A_{2} & := \frac{1}{N^{2}} \sum_{i \notin s} [G (t - m_{i} | x_{i}) - G^{2} (t - m_{i} | x_{i})] \\ = \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + O (n^{- 1} α) . \end{array}$

Thus,

$\begin{array}{l} var (\hat{F} (t) - F_{N} (t)) & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + O ({(n λ)}^{- 1} α) . \end{array}$

Variance of the generalized difference Kuo estimator

Note that

$\tilde{F} (t) - F_{N} (t) = \frac{1}{N} {\sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1) + (π_{j}^{- 1} - 1)] - \sum_{i \notin s} I (y_{i} \leq t)}$

so that

$\begin{array}{l} var (\tilde{F} (t) - F_{N} (t)) & = var (\frac{1}{N} \sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]) \\ + var (\frac{1}{N} \sum_{i \notin s} I (y_{i} \leq t)) \\ = B_{1} + A_{2}, \end{array}$

where $A_{2}$ is the same as in the variance of $\hat{F} (t),$ and where

$\begin{array}{l} B_{1} & := var (\frac{1}{N} \sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]) \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {[\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]}^{2} \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {[\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) (1 - \sum_{i \in s} {\tilde{w}}_{i, j})]}^{2} + O (λ n^{- 1}) \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α + λ n^{- 1}) \\ = A_{1} + O ({(n λ)}^{- 1} α + λ n^{- 1}) . \end{array}$

Thus,

$var (\tilde{F} (t) - F_{N} (t)) = var (\hat{F} (t) - F_{N} (t)) + O ({(n λ)}^{- 1} α + λ n^{- 1}) .$

Bias of the model-based estimator with modified fitted values

Let ${\hat{\hat{m}}}_{i} := \sum_{k \in s} w_{i, k} m_{k},$ $c_{i, j} :=1 - w_{j, j} + w_{i, j}$ and

$d_{i, j} := \frac{1}{c_{i, j}} [(1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + \sum_{k \in s, k \neq j} (w_{j, k} - w_{i, k}) ε_{k}] .$

Observe that $w_{i, j} = O_{i, j} ({(n λ)}^{- 1})$ so that

$y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i}$

is (asymptotically, as soon as $c_{i, j} >0)$ equivalent to

$ε_{j} \leq t - m_{i} + d_{i, j} .$

Since $d_{i, j}$ does not depend on $ε_{j},$ it follows that

$\begin{array}{l} E (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i})) & = E (I (ε_{j} \leq t - m_{i} + d_{i, j})) \\ = E (E (I (ε_{j} \leq t - m_{i} + d_{i, j}) | ε_{k}, k \neq j)) \\ = E (G (t - m_{i} + d_{i, j} | x_{j})) . \end{array} (A .1)$

Now, using the fact that

$d_{i, j} = (1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + \sum_{k \in s, k \neq j} (w_{j, k} - w_{i, k}) ε_{k} + R (d_{i, j}), (A .2)$

where

$E^{1 / 4} ({| R (d_{i, j}) |}^{4}) = O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}), (A .3)$

it is seen from (A.1) that

$\begin{array}{l} E (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i})) & = E (G (t - m_{i} + d_{i, j}) | x_{j}) \\ = G (t - m_{i} | x_{j}) + G^{(1,0)} (t - m_{i} | x_{j}) E (d_{i, j}) \\ + \frac{1}{2} G^{(2,0)} (t - m_{i} | x_{j}) E (d_{i, j}^{2}) + o_{i, j} (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .4)$

Thus,

$\begin{array}{l} E ({\hat{F}}^{*} (t) - F_{N} (t)) & = E (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i}) - I (y_{i} \leq t))) \\ = \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{i} | x_{j}) - G (t - m_{i} | x_{i})] \\ + \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) E (d_{i, j}) \\ + \frac{1}{2 N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(2, 0)} (t - m_{i} | x_{j}) E (d_{i, j}^{2}) + o (λ^{4} + {(n λ)}^{- 1}) \\ := C_{1} + C_{2} + C_{3} + o (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .5)$

Consider first $C_{1}$ and note that

$\begin{array}{l} C_{1} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{i} | x_{j}) - G (t - m_{i} | x_{i})] \\ = \frac{1}{2 N} \sum_{i \notin s} G^{(0, 2)} (t - m_{i} | x_{i}) \sum_{j \in s} w_{i, j} {(x_{j} - x_{i})}^{2} + o (λ^{2}) \\ = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h_{\bar{s}} (x) d x + o (λ^{2}) . \end{array}$

Consider next $C_{2} .$ (A.2) and (A.3) imply that

$\begin{array}{l} E (d_{i, j}) & = (1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \\ = (w_{j, j} - w_{i, j}) (t - m_{i}) + m_{j''} \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - m_{i''} \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2} \\ + o_{i, j} (λ^{2}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \\ = (w_{j, j} - w_{i, j}) (t - m_{i}) + (m_{j''} - m_{i''}) \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} \\ + m_{i''} (\sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) \\ + o_{i, j} (λ^{2}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \end{array}$

so that

$C_{2} = C_{2, a} + C_{2, b} + C_{2, c} + o (λ^{2}) + O (λ n^{- 1} + {(n λ)}^{- 3 / 2}),$

where

$\begin{array}{l} C_{2, a} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) (w_{j, j} - w_{i, j}) (t - m_{i}) \\ = \frac{1}{N} \sum_{i \notin s} G^{(1, 0)} (t - m_{i} | x_{i}) (t - m_{i}) \sum_{j \in s} w_{i, j} (w_{j, j} - w_{i, j}) + O (n^{- 1}) \\ = \frac{1}{n λ} \frac{N - n}{N} \frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) [h_{\bar{s}} (x) / h_{s} (x)] d x \\ + O ({(n λ)}^{- 1} λ^{- 1} α + n^{- 1}) \end{array}$

with $κ := \int_{- 1}^{1} K^{2} (u) d u,$

$\begin{array}{l} C_{2, b} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) (m_{j''} - m_{i''}) \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} \\ = o (λ^{2}) \end{array}$

and

$\begin{array}{l} C_{2, c} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) m_{i''} (\sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) \\ = \frac{1}{N} \sum_{i \notin s} G^{(1, 0)} (t - m_{i} | x_{i}) m_{i''} (\sum_{j \in s} w_{i, j} \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) + o (λ^{2}) \\ = o (λ^{2}) . \end{array}$

Consider finally $C_{3} .$ Note that from (A.2) and (A.3)

$E (d_{i, j}^{2}) = \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} σ_{k}^{2} + O_{i, j} (λ^{4} + {(n λ)}^{- 2}) (A .6)$

so that

$\begin{array}{l} C_{3} & = \frac{1}{2 N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(2, 0)} (t - m_{i} | x_{j}) \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} σ_{k}^{2} + O (λ^{4} + {(n λ)}^{- 2}) \\ = \frac{1}{2 N} \sum_{i \notin s} G^{(2, 0)} (t - m_{i} | x_{i}) σ_{i}^{2} \sum_{j \in s} w_{i, j} \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} + o ({(n λ)}^{- 1}) + O (λ^{4}) \\ = \frac{1}{n λ} \frac{N - n}{N} \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) [h_{\bar{s}} (x) / h_{s} (x)] d x + o ({(n λ)}^{- 1}) + O (λ^{4}) \end{array}$

with $θ := \int_{- 1}^{1} K (v) \int_{- 1}^{1} K (u + v) K (u) d u d v .$

Substituting the above expansions for $C_{1}, C_{2}$ and $C_{3}$ into (A.5) yields finally

$\begin{array}{l} E ({\hat{F}}^{*} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h_{\bar{s}} (x) d x \\ + \frac{1}{n λ} \frac{N - n}{N} [\frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) h_{s}^{- 1} (x) h_{\bar{s}} (x) d x \\ + \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) h_{s}^{- 1} (x) h_{\bar{s}} (x) d x] \\ + o (λ^{2} + {(n λ)}^{- 1}) . \end{array}$

Bias of the generalized difference estimator with modified fitted values

Let ${\tilde{d}}_{i, j}$ be the design-weighted counterpart of $d_{i, j}$ and observe that

$\begin{array}{l} {\tilde{F}}^{*} (t) - F_{N} (t) & = \frac{1}{N} [\sum_{i \notin s} \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t)) \\ + \sum_{i \in s} (1 - π_{i}^{- 1}) \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t))] . \end{array} (A .7)$

Adapting the proof that leads to (A.4), it is seen that the asymptotic expansion in (A.4) holds also with ${\tilde{d}}_{i, j}$ in place of $d_{i, j} .$ Adapting the remaining part of the proof finally leads to

$\begin{array}{l} E ({\tilde{F}}^{*} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h (x) d x \\ + \frac{1}{n λ} \frac{N - n}{N} [\frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) h_{s}^{- 1} (x) h (x) d x \\ + \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) h_{s}^{- 1} (x) h (x) d x] \\ + o (λ^{2} + {(n λ)}^{- 1}), \end{array}$

where

$h (x) := h_{\bar{s}} (x) + (1 - π^{- 1} (x)) h_{s} (x) .$

Variance of the model-based estimator with modified fitted values

Write

${\hat{F}}^{*} (t) - F_{N} (t) = \frac{1}{N} (\sum_{i \notin s} \sum_{j \in s} w_{i, j} I (ε_{j} \leq t - m_{i} + d_{i, j}) - \sum_{i \notin s} I (ε_{i} \leq t - m_{i}))$

and observe that

$var ({\hat{F}}^{*} (t) - F_{N} (t)) = D_{1} + D_{2} + D_{3},$

where

$D_{1} := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})),$

$D_{2} := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} \times cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}}))$

and where $D_{3} := A_{2}$ from the variance of the model-based Kuo estimator.

Consider $D_{1} .$ Observe that

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})) & = E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) \\ - E (G (t - m_{i_{1}} + d_{i_{1}, j} | x_{j})) E (G (t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) . \end{array} (A .8)$

Since

$| (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j}) - (t - m_{i_{1}} \land t - m_{i_{2}}) | \leq | d_{i_{1}, j} | + | d_{i_{2}, j} |,$

it follows from (A.6) that

$E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) = G (t - m_{i_{1}} \land t - m_{i_{2}} | x_{j}) + O_{i_{1}, i_{2}, j} (λ^{2} + {(n λ)}^{- 1 / 2}) . (A .9)$

Moreover, from (A.1), (A.4) and (A.6) it follows that

$\begin{array}{l} E (G (t - m_{i} + d_{i, j} | x_{j})) = & G (t - m_{i} | x_{j}) + O_{i, j} (λ^{2} + {(n λ)}^{- 1 / 2}) . \end{array} (A .10)$

Using (A.9) and (A.10) to get an asymptotic expansion for the covariance in (A.8), and substituting the outcome into the definition of $D_{1}$ yields

$\begin{array}{l} D_{1} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})) \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) \\ - E (G (t - m_{i_{1}} + d_{i_{1}, j} | x_{j})) E (G (t - m_{i_{2}} + d_{i_{2}, j} | x_{j}))] \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{i_{1}} \land t - m_{i_{2}} | x_{j}) - G (t - m_{i_{1}} | x_{j}) G (t - m_{i_{2}} | x_{j})] \\ + O (λ^{2} n^{- 1} + {(n λ)}^{- 1 / 2} n^{- 1}) \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {(\sum_{i \notin s} w_{i, j})}^{2} + O (λ n^{- 1} + {(n λ)}^{- 1 / 2} n^{- 1}) \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α + n^{- 1} λ + n^{- 1} {(n λ)}^{- 1 / 2}) . \end{array} (A .11)$

Consider next

Since

$cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) =0$

if $| x_{i_{1}} - x_{i_{2}} | >2 λ,$ it follows that rest terms $R_{i_{1}, j_{1}, i_{2}, j_{2}},$ whose contribution to the above covariance is of order $O_{i_{1}, j_{1}, i_{2}, j_{2}} (β)$ for some sequence $β$ that goes to zero, contribute to $D_{2}$ a term of order $O (λ β) .$ Now, let

$b_{i, j_{1}, j_{2}} := c_{i, j_{1}}^{- 1} (w_{j_{1}, j_{2}} - w_{i, j_{2}}),$

$a_{i, j_{1}, j_{2}} := t - m_{i} + d_{i, j_{1}} - b_{i, j_{1}, j_{2}} ε_{j_{2}}$

and note that

$t - m_{i} + d_{i, j_{1}} = a_{i, j_{1}, j_{2}} + b_{i, j_{1}, j_{2}} ε_{j_{2}} .$

Since $a_{i, j_{1}, j_{2}}$ does not depend on $ε_{j_{1}}$ and $ε_{j_{2}},$ it follows that

$\begin{array}{l} E (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}) I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) \\ = E (E (I (ε_{j_{1}} \leq a_{i_{1}, j_{1}, j_{2}} + b_{i_{1}, j_{1}, j_{2}} ε_{j_{2}}) I (ε_{j_{2}} \leq a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε_{j_{1}}) | ε_{k}, k \neq j_{1}, j_{2})) \\ = E (\int_{- \infty}^{ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}} G (a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε | x_{j_{2}}) d G (ε | x_{j_{1}})) \\ + E (\int_{- \infty}^{ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*}} G (a_{i_{1}, j_{1}, j_{2}} + b_{i_{1}, j_{1}, j_{2}} ε | x_{j_{1}}) d G (ε | x_{j_{2}})) \\ - E (G (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} | x_{j_{1}}) G (ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*} | x_{j_{2}})), \end{array} (A .12)$

where

$ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} := \frac{a_{i_{1,} j_{1}, j_{2}} + a_{i_{2}, j_{2}, j_{1}} b_{i_{1}, j_{1}, j_{2}}}{1 - b_{i_{1}, j_{1}, j_{2}} b_{i_{2}, j_{2}, j_{1}}} .$

Note that the two expectations in the third and fourth lines in (A.12) are the same if $i_{1}$ and $j_{1}$ are interchanged with $i_{2}$ and $j_{2},$ respectively. Thus it suffices to analyze the first expectation. Using the fact that

$ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} = t - m_{i_{1}} + d_{i_{1}, j_{1}} + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}} - ε_{j_{2}}) + R (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}),$

where

$E^{1 / 4} ({| R (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}) |}^{4}) = O_{i_{1}, i_{2}, j_{1}, j_{2}} (λ n^{- 1} + {(n λ)}^{- 3 / 2}),$

it is seen that

$\begin{array}{l} E (\int_{- \infty}^{ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}} G (a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε | x_{j_{2}}) d G (ε | x_{j_{1}})) \\ = G (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) [E (d_{i_{1}, j_{1}}) + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}})] \\ + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}) + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) b_{i_{2}, j_{2}, j_{1}} \int_{- \infty}^{t - m_{i_{1}}} ε d G (ε | x_{j_{1}}) \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}}^{2}) + \frac{1}{2} G^{(2, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}^{2}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}} d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}), \end{array} (A .13)$

and that

$\begin{array}{l} E (G (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} | x_{j_{1}}) G (ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*} | x_{j_{2}})) \\ = G (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) [E (d_{i_{1}, j_{1}}) + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}})] \\ + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) [E (d_{i_{2}, j_{2}}) + b_{i_{2}, j_{2}, j_{1}} (t - m_{i_{1}})] \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}}^{2}) \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}^{2}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}} d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .14)$

Using the asymptotic expansions in (A.4), (A.13) and (A.14) yields

$\begin{array}{l} cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) \\ = G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) b_{i_{2}, j_{2}, j_{1}} γ_{i_{1}, j_{1}} + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) b_{i_{1}, j_{1}, j_{2}} γ_{i_{2}, j_{2}} \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) cov (d_{i_{1}, j_{1}}, d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}), \end{array} (A .15)$

where

$γ_{i, j} := \int_{- \infty}^{t - m_{i}} ε d G (ε | x_{j}) .$

Now observe that

$b_{i, j_{1}, j_{2}} = w_{j_{1}, j_{2}} - w_{i, j_{2}} + O_{i, j_{1}, j_{2}} ({(n λ)}^{- 2})$

and that

$\begin{array}{l} cov (d_{i_{1}, j_{1}}, d_{i_{2}, j_{2}}) & = \frac{1}{c_{i_{1}, j_{1}} c_{i_{2}, j_{2}}} \sum_{k \in s; k \neq j_{1}, j_{2}} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} \\ = \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} + O_{i_{1}, i_{2}, j_{1}, j_{2}} ({(n λ)}^{- 2}) \end{array}$

so that

$D_{2} =2 D_{2 a} + D_{2 b} + o (λ^{5} + n^{- 1}), (A .16)$

where

$\begin{array}{l} D_{2 a} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) (w_{j_{1}, j_{2}} - w_{i_{1}, j_{2}}) γ_{i_{2}, j_{2}} \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) (w_{j_{1}, j_{2}} - w_{i_{1}, j_{2}}) γ_{i_{2}, j_{2}} + O (n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{j_{2} \in s} G^{(1, 0)} (t - m_{j_{2}} | x_{j_{2}}) γ_{j_{2}, j_{2}} [\sum_{j_{1} \in s} w_{j_{1}, j_{2}} \sum_{i_{1} \notin s} w_{i_{1}, j_{1}} \sum_{i_{2} \notin s} w_{i_{2}, j_{2}} - {(\sum_{i \notin s} w_{i, j_{2}})}^{2}] \\ + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = O ({(n λ)}^{- 1} α + n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \end{array} (A .17)$

and

$\begin{array}{l} D_{2 b} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) \\ \times \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) \\ \times \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} + O (n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{k \in s} σ_{k}^{2} {[G^{(1, 0)} (t - m_{k} | x_{k})]}^{2} {(\sum_{i \notin s} \sum_{j \in s} w_{i, j} (w_{j, k} - w_{i, k}))}^{2} + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{k \in s} σ_{k}^{2} {[G^{(1, 0)} (t - m_{k} | x_{k})]}^{2} {(\sum_{j \in s} w_{j, k} \sum_{i \notin s} w_{i, j} - \sum_{i \notin s} w_{i, k})}^{2} + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = O ({(n λ)}^{- 1} α + n^{- 1} λ) . \end{array} (A .18)$

Putting everything together finally yields

$\begin{array}{l} var ({\hat{F}}^{*} (t) - F_{N} (t)) & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + o (λ^{5} + n^{- 1}) . \end{array}$

Variance of the generalized difference estimator with modified fitted values

In view of (A.7), we shall show that

$var ({\tilde{F}}^{*} (t) - F_{N} (t)) = var ({\hat{F}}^{*} (t) - F_{N} (t)) + o (n^{- 1}) (A .19)$

by showing that

$var (\frac{1}{N} \sum_{i \in s} (1 - π_{i}^{- 1}) \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t))) = o (n^{- 1}) . (A .20)$

To prove (A.20) observe that the variance on the left hand side may be written as

$E_{1} + E_{2} + E_{3} - 2 E_{4} - 2 E_{5},$

where

$E_{1} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j \in s} {\tilde{w}}_{i_{1}, j} {\tilde{w}}_{i_{2}, j} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + {\tilde{d}}_{i_{2}, j})),$

$E_{2} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} {\tilde{w}}_{i_{1}, j} {\tilde{w}}_{i_{2}, j_{2}} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + {\tilde{d}}_{i_{2}, j_{2}})),$

$\begin{array}{l} E_{3} & := \frac{1}{N^{2}} \sum_{i \in s} {(1 - π_{i}^{- 1})}^{2} var (I (ε_{i} \leq t - m_{i})), \end{array}$

$\begin{array}{l} E_{4} & := \frac{1}{N^{2}} \sum_{i \in s} \sum_{j \in s} {\tilde{w}}_{i_{1}, j} (1 - π_{i}^{- 1}) (1 - π_{j}^{- 1}) cov (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}), I (ε_{j} \leq t - m_{j})), \end{array}$

and finally

$E_{5} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j \in s, j \neq i_{2}} {\tilde{w}}_{i_{1}, j} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) .$

To begin with, consider $E_{1}$ and $E_{2} .$ Observe that except for (i) the fact that the summation indexes $i_{1}$ and $i_{2}$ range over $s$ instead of the complement of $s$ in $U,$ (ii) the presence of the factors $(1 - π_{i}^{- 1})$ and (iii) the fact that the $w_{i, j} ’ s$ and the $d_{i, j} ’ s$ are substituted by their design-weighted counterparts ${\tilde{w}}_{i, j}$ and ${\tilde{d}}_{i, j},$ $E_{1}$ and $E_{2}$ are the same as $D_{1}$ and $D_{2}$ from $var ({\hat{F}}^{*} (t) - F_{N} (t)),$ respectively. Adapting the proofs that lead to the asymptotic expansions for $D_{1}$ and $D_{2}$ shows thus that

$\begin{array}{l} E_{1} & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] {[1 - π^{- 1} (x)]}^{2} h_{s} (x) d x + o (n^{- 1}) \end{array}$

and that

$E_{2} = o (λ^{5} + n^{- 1}) .$

As for $E_{3}$ it is immediately seen that

$E_{3} = E_{1} + o (n^{- 1}),$

while in order to deal with $E_{4}$ and $E_{5}$ we shall need asymptotic expansions for

$cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) (A .21)$

for the case when $j = i_{2}$ and the case when $j \neq i_{2} .$ In the former case we may employ arguments similar to those for proving (A.9) and (A.10), which lead to

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{j} \leq t - m_{j})) \\ = G (t - m_{i_{1}} \land t - m_{j} | x_{j}) - G (t - m_{i_{1}} | x_{j}) G (t - m_{j} | x_{j}) + O (λ^{2} + {(n λ)}^{- 1 / 2}) . \end{array}$

When $j \neq i_{2},$ on the other hand, the covariance in (A.21) is different from zero only if $| x_{j} - x_{i_{2}} | \leq λ$ or $| x_{i_{1}} - x_{i_{2}} | \leq λ,$ and adapting (A.12) it can be shown that

$\begin{array}{l} E (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}) I (ε_{i_{2}} \leq t - m_{i_{2}})) \\ = E (E (I (ε_{j} \leq {\tilde{a}}_{i_{1}, j, i_{2}} + {\tilde{b}}_{i_{1}, j, i_{2}} ε_{i_{2}}) I (ε_{i_{2}} \leq t - m_{i_{2}}) | ε_{k}, k \neq i, j)) \\ = E (\int_{- \infty}^{t - m_{i_{2}}} G ({\tilde{a}}_{i_{1}, j, i_{2}} + {\tilde{b}}_{i_{1}, j, i_{2}} ε | x_{j}) d G (ε | x_{i_{2}})) \\ = G (t - m_{i_{1}} | x_{j}) G (t - m_{i_{2}} | x_{i_{2}}) + G (t - m_{i_{2}} | x_{i_{2}}) G^{(1, 0)} (t - m_{i_{1}} | x_{j}) E (d_{i_{1}, j}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j}) {\tilde{b}}_{i_{1}, j, i_{2}} γ_{i_{2}, i_{2}} + \frac{1}{2} G (t - m_{i_{2}} | x_{i_{2}}) G^{(2, 0)} (t - m_{i_{1}} | x_{j}) E (d_{i_{1}, j}^{2}) \\ + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}), \end{array}$

where ${\tilde{a}}_{i, j, k}$ and ${\tilde{b}}_{i, j, k}$ are the design-weighted counterparts of $a_{i, j, k}$ and $b_{i, j, k},$ respectively. Adapting also (A.4) to account for the design-weights, it is seen that

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) & = G^{(1, 0)} (t - m_{i_{1}} | x_{j}) {\tilde{b}}_{i_{1}, j, i_{2}} γ_{i_{2}, i_{2}} + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}) \\ = G^{(1, 0)} (t - m_{i} | x_{j}) ({\tilde{w}}_{j, i_{2}} - {\tilde{w}}_{i_{1}, i_{2}}) γ_{i_{2}, i_{2}} + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}) \end{array}$

so that (cfr. the steps that lead to the asymptotic expansions of the terms $D_{1}$ and $D_{2}$ in the variance of the model-based two-step estimator)

$E_{4} = E_{1} + o (n^{- 1})$

and

$E_{5} = o (λ^{5} + n^{- 1}) .$

This completes the proof of (A.20) and thus (A.19) follows.

References

Breidt, F.J., and Opsomer, J.D. (2000). Local polynomial regression estimators in survey sampling. The Annals Statistics, 28(4), 1026-1053.

Chambers, R.L., and Clark, R. (2012). An Introduction to Model-Based Survey Sampling with Applications, Oxford Statistical Science Series 37.

Chambers, R.L., and Dunstan, R. (1986). Estimating distribution functions from survey data. Biometrika, 73(3), 597-604.

Chambers, R.L., Dorfman, A.H. and Wehrly, T.E. (1993). Bias robust estimation in finite populations using non-parametric calibration. Journal of the American Statistical Association, 88(421), 268-277.

Chen, J., and Wu, C. (2002). Estimation of distribution function and quantiles using the model-calibrated pseudo empirical likelihood method. Statistica Sinica, 12, 1223-1239.

Dorfman, A.H., and Hall, P. (1993). Estimators of the finite population distribution function using nonparametric regression. The Annals of Statistics, 21(3), 1452-1475.

Fan, J., and Gijbels, I. (1992). Variable bandwidth and local linear regression smoothers. The Annals of Statistics, 20(4), 2008-2036.

Hansen, B.E. (2008). Uniform convergence rates for kernel estimation with dependent data. Econometric Theory, 24, 726-748.

Johnson, A.A., Breidt, F.J. and Opsomer, J.D. (2008). Estimating distribution functions from survey data using nonparametric regression. Journal of Statistical Theory and Practice, 2(3), 419-431.

Kuo, L. (1988). Classical and prediction approaches to estimating distribution functions from survey data. In Proceedings of the Survey Research Methods Section, American Statistical Association, Alexandria, VA, 280-285.

Montanari, G.E., and Ranalli, M.G. (2005). Nonparametric model calibration estimation in survey sampling. Journal of the American Statistical Association, 100(472), 1429-1442.

Rao, J.N.K., Kovar, J.G. and Mantel, H.J. (1990). On estimating distribution functions and quantiles from survey data using auxiliary information. Biometrika, 77(2), 365-375.

Rueda, M., Martínez, S., Martínez, H. and Arcos, A. (2007). Estimation of the distribution function with calibration methods. Journal of Statistical Planning and Inference, 137(2), 435-448.

Rueda, M., Sànchez-Borrego, I., Arcos, A. and Martínez, S. (2010). Model-calibration estimation of the distribution function using nonparametric regression. Metrika, 71(1), 33-44.

Särndal, C.-E., Swensson, B. and Wretman, J. (1992). Model Assisted Survey Sampling, New York: Springer.

Wang, J.C., and Opsomer, J.D. (2011). On asymptotic normality and variance estimation for nondifferentiable survey estimators. Biometrika, 98(1), 91-106.

Wu, C. (2003). Optimal calibration estimators in survey sampling. Biometrika, 90(4), 937-951.

Wu, C., and Sitter, R.R. (2001). A model-calibration approach to using complete auxiliary information from survey data. Journal of the American Statistical Association, 96(453), 185-193.

ISSN : 1492-0921

Editorial policy

Survey Methodology publishes articles dealing with various aspects of statistical development relevant to a statistical agency, such as design issues in the context of practical constraints, use of different data sources and collection techniques, total survey error, survey evaluation, research in survey methodology, time series analysis, seasonal adjustment, demographic studies, data integration, estimation and data analysis methods, and general survey systems development. The emphasis is placed on the development and evaluation of specific methodologies as applied to data collection or the data themselves. All papers will be refereed. However, the authors retain full responsibility for the contents of their papers and opinions expressed are not necessarily those of the Editorial Board or of Statistics Canada.

Submission of Manuscripts

Survey Methodology is published twice a year in electronic format. Authors are invited to submit their articles in English or French in electronic form, preferably in Word to the Editor, (statcan.smj-rte.statcan@canada.ca, Statistics Canada, 150 Tunney’s Pasture Driveway, Ottawa, Ontario, Canada, K1A 0T6). For formatting instructions, please see the guidelines provided in the journal and on the web site (www.statcan.gc.ca/SurveyMethodology).

Note of appreciation

Canada owes the success of its statistical system to a long-standing partnership between Statistics Canada, the citizens of Canada, its businesses, governments and other institutions. Accurate and timely statistical information could not be produced without their continued co-operation and goodwill.

Standards of service to the public

Statistics Canada is committed to serving its clients in a prompt, reliable and courteous manner. To this end, the Agency has developed standards of service which its employees observe in serving its clients.

Copyright

Published by authority of the Minister responsible for Statistics Canada.

Use of this publication is governed by the Statistics Canada Open Licence Agreement.

Catalogue No. 12-001-X

Frequency: semi-annual

Ottawa

Date modified:: 2016-06-22

Language selection

Search and menus

Search

A comparison between nonparametric estimators for finite population distribution functions 5. Simulation studyA comparison between nonparametric estimators for finite population distribution functions 5. Simulation study

Acknowledgements

Appendix

Bias of the model-based Kuo estimator

Bias of the generalized difference Kuo estimator

Variance of the model-based Kuo estimator

Variance of the generalized difference Kuo estimator

Bias of the model-based estimator with modified fitted values

Bias of the generalized difference estimator with modified fitted values

Variance of the model-based estimator with modified fitted values

Variance of the generalized difference estimator with modified fitted values

References