Une comparaison d’estimateurs non paramétriques pour les fonctions de répartition de populations finies 5. Étude en simulationUne comparaison d’estimateurs non paramétriques pour les fonctions de répartition de populations finies 5. Étude en simulation

À la présente section, nous analysons certains résultats de simulation. Notre objectif est de comparer l’efficacité par rapport au plan de sondage des estimateurs des fonctions de répartition présentés à la section 2 et des estimateurs de la variance présentés à la section 4. Les résultats des simulations s’appliquent à l’échantillonnage aléatoire simple sans remise et à l’échantillonnage de Poisson avec probabilités d’inclusion inégales. À titre de référence, nous avons également inclus dans l’étude en simulation l’estimateur de la fonction de répartition de Horvitz-Thompson

${\hat{F}}_{π} (t) := \frac{1}{N} \sum_{j \in s} π_{j}^{- 1} I (y_{j} \leq t)$

et l’estimateur de variance correspondant

$\tilde{V} ({\hat{F}}_{π} (t)) := \frac{1}{N^{2}} \sum_{i, j \in s} \frac{π_{i, j} - π_{i} π_{j}}{π_{i, j} π_{i} π_{j}} I (y_{i} \leq t) I (y_{j} \leq t) .$

Nous avons considéré des populations artificielles ainsi que réelles. Les premières ont été obtenues en générant $N = 1 000$ valeurs $x_{i}$ à partir de variables aléatoires i.i.d. de loi uniforme avec support sur l’intervalle $(0, 1)$ et en les combinant avec trois types de fonction de régression $m (x)$ et deux types de composantes de l’erreur $ε_{i} .$ Les fonctions de régression sont i) $m (x) = 0$ (uniforme), ii) $m (x) = 10 x$ (linéaire) et iii) $m (x) = 10 x^{1 / 4}$ (concave), tandis que les composantes de l’erreur $ε_{i}$ sont soit des réalisations indépendantes tirées d’une loi $t$ de Student unique à $v = 5$ dl, ou des réalisations indépendantes tirées de $N$ lois $t$ de Student non centrales décalées à $v = 5$ dl et avec paramètres de non-centralité donnés par $μ = 15 x_{i} .$ Les décalages appliqués aux composantes de l’erreur dans le dernier cas font en sorte que les moyennes des lois $t$ de Student non centrales à partir desquelles elles sont générées soient nulles. Les populations artificielles sont présentées aux figures 5.1 à 5.3. En ce qui concerne les populations réelles, nous avons pris la population $M U 284$ de municipalités suédoises de Särndal et coll. (1992) (taille de la population $N = 284)$ et considéré le logarithme naturel de $R M T 85 =$ Revenus de l’imposition municipale de 1985 (en millions de couronnes) comme variable étudiée $Y,$ et le logarithme naturel de $P 85 =$ population de 1985 (en milliers) ou de $R E V 84 =$ valeurs immobilières selon les évaluations de 1984 (en millions de couronnes) comme variable auxiliaire $X .$ Les populations réelles sont présentées à la figure 5.4.

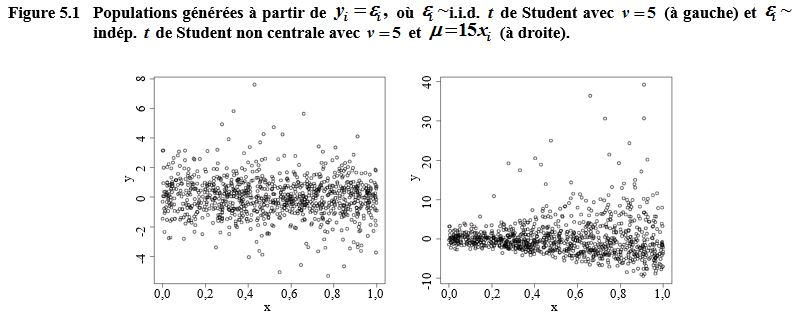
Figure 5.1 de l'article 14541

Description de la figure 5.1

Figure composée de deux graphiques en nuages de point de $y$ en fonction de $x,$ chacun représentant une population artificielle. Le premier graphique est la population générée à partir de $y_{i} = ε_{i},$ où $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν = 5.$ L’axe des y va de -4 à 8 et l’axe des x va de 0,0 à 1,0. Le nuage de point est centré autour de $y = 0.$ Le deuxième graphique en nuage de points est la population générée à partir de $y_{i} = ε_{i}$ et $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν = 5$ et $μ = 15 x_{i} .$ L’axe des y va de -10 à 40 et l’axe des x va de 0,0 à 1,0. Le nuage de point est concentré autour de $y = 0$ pour de petites valeurs de $x .$ Plus $x$ augmente, plus la dispersion des points augmente.

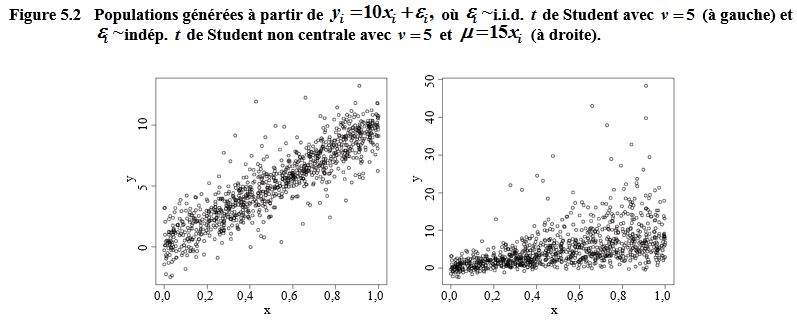
Figure 5.2 de l'article 14541

Description de la figure 5.2

Figure composée de deux graphiques en nuages de point de $y$ en fonction de $x,$ chacun représentant une population artificielle. Le premier graphique est la population générée à partir de $y_{i} = 10 x_{i} + ε_{i},$ où $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν = 5.$ L’axe des y va de 0 à 10 et l’axe des x va de 0,0 à 1,0. Le nuage de point montre une relation linéaire croissante entre $x$ et $y .$ Le deuxième graphique en nuage de points est la population générée à partir de $y_{i} = ε_{i}$ et $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν = 5$ et $μ = 15 x_{i} .$ L’axe des y va de 0 à 50 et l’axe des x va de 0,0 à 1,0. Le nuage de point montre une relation linéaire croissante entre $x$ et $y .$ Plus $x$ augmente, plus la dispersion des points augmente.

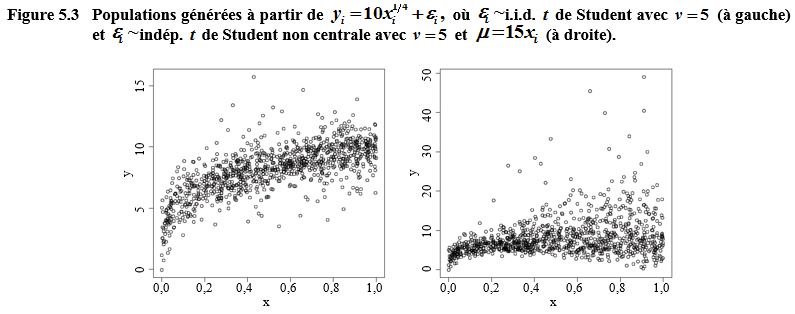
Figure 5.3 de l'article 14541

Description de la figure 5.3

Figure composée de deux graphiques en nuages de point de $y$ en fonction de $x,$ chacun représentant une population artificielle. Le premier graphique est la population générée à partir de $y_{i} = 10 x_{i}^{1 / 4} + ε_{i},$ où $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν = 5.$ L’axe des y va de 0 à 15 et l’axe des x va de 0,0 à 1,0. Le nuage de point montre une relation concave croissante entre $x$ et $y .$ Le deuxième graphique en nuage de points est la population générée à partir de $y_{i} = ε_{i}$ et $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν = 5$ et $μ = 15 x_{i} .$ L’axe des y va de 0 à 50 et l’axe des x va de 0,0 à 1,0. Le nuage de point montre une relation concave croissante entre $x$ et $y .$ Plus $x$ augmente, plus la dispersion des points augmente.

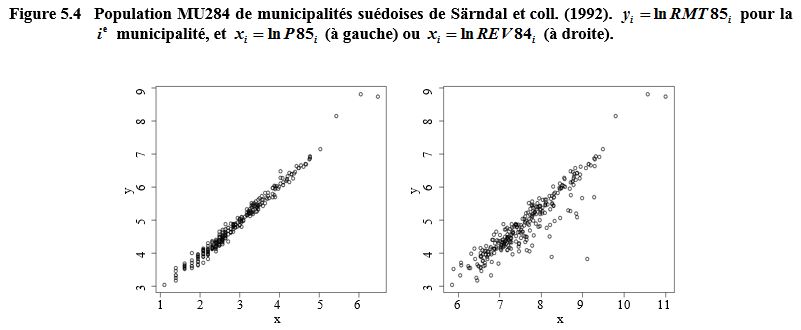
Figure 5.4 de l'article 14541

Description de la figure 5.4

Figure composée de deux graphiques en nuages de point de $y$ en fonction de $x,$ chacun représentant une population réelle, population $M U 284$ de municipalités suédoises de Särndal et coll. (1992). Dans le premier graphique, $y_{i} = \ln R M T 85_{i}$ pour la $i^{e}$ municipalité et $x_{i} = \ln P 85_{i} .$ L’axe des y va de 3 à 9 et l’axe des x va de 1 à 6. Le nuage de point montre une relation linéaire croissante entre $x$ et $y .$ Dans le deuxième graphique, $y_{i} = \ln R M T 85_{i}$ pour la $i^{e}$ municipalité et $x_{i} = \ln R E V 84_{i} .$ L’axe des y va de 3 à 9 et l’axe des x va de 6 à 11. Le nuage de point montre une relation linéaire croissante entre $x$ et $y,$ mais plus dispersée.

Pour chaque population, nous avons sélectionné indépendamment $B = 1 000$ échantillons. Pour le tirage d’échantillons à partir des populations artificielles, en cas d’échantillonnage aléatoire simple sans remise, nous avons fixé la taille d’échantillon à $n = 100,$ et en cas d’échantillonnage de Poisson, nous avons fixé la taille d’échantillon espérée à $n^{*} = 100$ et fait en sorte que les probabilités d’inclusion dans l’échantillon soient proportionnelles aux écarts-types des lois $t$ de Student non centrales décalées susmentionnées. Pour le tirage d’échantillons dans les populations réelles, nous avons fixé la taille d’échantillon à $n = 30$ en cas d’échantillonnage aléatoire simple sans remise. Pour l’échantillonnage de Poisson, nous avons fixé la taille d’échantillon espérée à $n^{*} = 30$ et fait en sorte que les probabilités d’inclusion dans l’échantillon soient proportionnelles aux valeurs absolues des résidus des régressions linéaires par les moindres carrés des valeurs $y_{i}$ de la population sur les valeurs $x_{i}$ de la population.

Comme pour la définition des estimateurs non paramétriques, nous avons utilisé la fonction noyau d’Epanechnikov $K (u) : = 0,75 (1 - u^{2})$ avec $λ = 0,15$ ou $λ = 0,3$ pour les échantillons tirés des populations artificielles et la fonction noyau gaussienne $K (u) : = 1 / \sqrt{2 π} e^{- (1 / 2) u^{2}}$ avec $λ = 1$ ou $λ = 2$ pour les échantillons tirés des populations réelles. Dans les tableaux présentant les résultats des simulations, les estimateurs non paramétriques correspondant aux petites et aux grandes valeurs de fenêtre de lissage sont désignés par un $s$ (pour small) ou par un $l$ (pour large), respectivement, dans l’indice inférieur. Nous avons recouru à la fonction noyau gaussienne pour les échantillons tirés des populations réelles afin d’éviter les problèmes de singularité qui se posent en cas de vides dans le jeu de valeurs $x_{i}$ échantillonnées. De tels vides sont nettement plus susceptibles d’exister dans le cas des populations réelles que dans celui des populations artificielles, parce que les lois des variables auxiliaires sont asymétriques dans les premières. En fait, dans les populations artificielles, les estimateurs non paramétriques étaient bien définis pour chacun des $B = 1 000$ échantillons sélectionnés selon le plan d’échantillonnage aléatoire simple sans remise. Pour le plan d’échantillonnage de Poisson, par contre, 47 des $B = 1 000$ échantillons simulés étaient tels que les estimateurs non paramétriques avec la petite valeur de fenêtre de lissage n’ont pas pu être calculés et seulement un de ces échantillons était tel que les estimateurs non paramétriques avec la grande valeur de fenêtre de lissage étaient indéfinis. Les résultats des simulations s’appliquant aux estimateurs non paramétriques dans les tableaux 5.2 et 5.5 tiennent compte uniquement des échantillons pour lesquels les estimateurs étaient bien définis et sont donc fondés sur un peu moins que les $B = 1 000$ réalisations.

Les tableaux 5.1 à 5.4 donnent le biais simulé (BIAIS) et la racine carrée de l’erreur quadratique moyenne simulée (REQM) pour chaque estimateur de la fonction de répartition à différents niveaux de $t$ auxquels $F_{N} (t)$ a été estimée : en se basant, par exemple, sur les valeurs ${\tilde{F}}_{b} (t),$ $b = 1, 2, \dots, B,$ tirées de l’estimateur $\tilde{F} (t),$

$BIAIS : = \frac{1}{B} \sum_{b = 1}^{B} ({\tilde{F}}_{b} (t) - F_{N} (t)) \times 10 000$

$REQM : = \sqrt{\frac{1}{B} \sum_{b = 1}^{B} {({\tilde{F}}_{b} (t) - F_{N} (t))}^{2}} \times 10 000.$

La REQM montre que les estimateurs fondés sur les valeurs prédites modifiées sont habituellement plus efficaces. Dans le cas de l'échantillonnage dans les populations réelles, l'augmentation des REQM est parfois assez grande. Comme prévu, les estimateurs fondés sur le modèle ont tendance à être plus efficaces que les estimateurs par la différence généralisée sous échantillonnage aléatoire simple sans remise quand les deux types d’estimateurs sont approximativement sans biais. Sous échantillonnage de Poisson, le BIAIS des estimateurs fondés sur le modèle augmente, mais demeure néanmoins concurrentiel. Une plus grande variabilité des probabilités d’inclusion dans l’échantillon modifierait certainement ce résultat, car elle augmenterait le BIAIS des estimateurs fondés sur le modèle. Les résultats des simulations ne doivent donc pas être considérés comme contredisant Johnson, Breidt et Opsomer (2008) qui se prononcent en faveur des estimateurs par la différence généralisée (appelés estimateurs assistés par modèle dans leur article), soutenant qu’il s’agit d’« un bon choix global pour les estimateurs de la fonction de répartition ».

Tableau 5.1
Populations artificielles (taille de population $N = 1 000) .$ BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage aléatoire simple sans remise. Taille d’échantillon $n = 100$ Sommaire du tableau
Le tableau montre les résultats de Tableau 5.1
Populations artificielles (taille de population XXXX). BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage aléatoire simple sans remise. Taille d’échantillon XXXX
XXXX , XXXX, BIAIS , REQM et REQM , calculées selon XXXX avec XXXX i.i.d. de Student centrale XXXX avec XXXX, XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX, XXXX avec XXXX i.i.d. de Student XXXX avec XXXX, XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX, XXXX avec XXXX i.i.d. de Student XXXX avec XXXX et XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student centrale avec $ν =5$
${\hat{F}}_{s} (t)$	6	216	-3	433	31	512	23	434	12	207
${\hat{F}}_{l} (t)$	15	219	10	430	0	502	-10	429	3	213
${\hat{F}}_{s}^{*} (t)$	6	209	-30	411	22	484	22	414	3	200
${\hat{F}}_{l}^{*} (t)$	15	214	-9	409	10	477	1	407	-10	207
${\tilde{F}}_{s} (t)$	6	213	8	425	24	504	-4	430	8	207
${\tilde{F}}_{l} (t)$	6	210	10	417	22	494	-8	422	6	206
${\tilde{F}}_{s}^{*} (t)$	8	213	9	426	25	503	-5	432	5	206
${\tilde{F}}_{l}^{*} (t)$	7	210	10	417	23	494	-6	424	4	206
${\tilde{F}}_{π} (t)$	7	208	11	411	19	489	-5	417	6	200
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	26	225	33	376	8	477	26	419	33	209
${\hat{F}}_{l} (t)$	52	236	23	374	-5	475	38	421	29	213
${\hat{F}}_{s}^{*} (t)$	20	195	-29	351	-89	471	11	407	30	202
${\hat{F}}_{l}^{*} (t)$	36	201	-11	357	-94	473	28	410	21	204
${\tilde{F}}_{s} (t)$	8	211	11	370	-7	473	4	415	16	211
${\tilde{F}}_{l} (t)$	5	208	8	367	-5	468	5	411	16	212
${\tilde{F}}_{s}^{*} (t)$	11	210	11	372	-11	475	4	416	15	210
${\tilde{F}}_{l}^{*} (t)$	7	208	11	368	-7	468	8	412	15	211
${\tilde{F}}_{π} (t)$	1	211	1	391	-6	477	8	399	18	210
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
${\hat{F}}_{s} (t)$	32	201	25	275	13	250	-14	264	-36	217
${\hat{F}}_{l} (t)$	114	250	152	304	12	236	-180	312	-86	242
${\hat{F}}_{s}^{*} (t)$	-50	165	12	226	51	216	26	230	13	172
${\hat{F}}_{l}^{*} (t)$	-46	155	-14	199	69	195	23	211	17	156
${\tilde{F}}_{s} (t)$	-5	186	4	275	15	248	11	269	-2	201
${\tilde{F}}_{l} (t)$	-5	184	7	274	17	250	5	269	-2	196
${\tilde{F}}_{s}^{*} (t)$	-10	180	5	275	16	245	14	266	-1	200
${\tilde{F}}_{l}^{*} (t)$	-9	176	3	272	15	242	13	262	-1	194
${\tilde{F}}_{π} (t)$	-7	203	14	413	37	472	17	405	1	206
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	24	204	23	351	27	403	26	382	29	208
${\hat{F}}_{l} (t)$	94	242	135	372	51	392	13	380	15	212
${\hat{F}}_{s}^{*} (t)$	55	182	-9	301	-18	368	-23	359	37	202
${\hat{F}}_{l}^{*} (t)$	124	210	-31	278	-63	363	-8	356	48	200
${\tilde{F}}_{s} (t)$	-2	194	-4	349	11	401	18	377	13	208
${\tilde{F}}_{l} (t)$	-2	190	-5	345	12	398	17	374	11	209
${\tilde{F}}_{s}^{*} (t)$	0	191	-5	352	14	401	20	376	13	207
${\tilde{F}}_{l}^{*} (t)$	-1	189	-6	344	13	397	18	375	12	209
${\tilde{F}}_{π} (t)$	-4	205	-5	401	21	470	24	401	14	207
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
${\hat{F}}_{s} (t)$	81	207	44	316	17	384	-2	376	23	203
${\hat{F}}_{l} (t)$	138	258	183	356	35	367	-50	374	8	208
${\hat{F}}_{s}^{*} (t)$	7	146	-14	274	16	352	-8	358	15	197
${\hat{F}}_{l}^{*} (t)$	9	144	10	246	-2	323	-18	339	24	186
${\tilde{F}}_{s} (t)$	3	175	3	319	10	383	17	374	10	203
${\tilde{F}}_{l} (t)$	0	178	5	316	11	380	17	370	8	202
${\tilde{F}}_{s}^{*} (t)$	1	167	5	320	12	383	17	374	9	203
${\tilde{F}}_{l}^{*} (t)$	-1	164	6	316	13	379	20	368	8	201
${\tilde{F}}_{π} (t)$	4	209	11	412	25	477	27	422	10	200
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	59	234	95	402	66	455	51	395	26	208
${\hat{F}}_{l} (t)$	94	259	190	441	147	467	98	400	16	212
${\hat{F}}_{s}^{*} (t)$	30	184	33	343	-123	435	-34	385	40	203
${\hat{F}}_{l}^{*} (t)$	57	201	58	331	-148	437	2	382	34	203
${\tilde{F}}_{s} (t)$	1	205	7	386	12	449	17	392	13	208
${\tilde{F}}_{l} (t)$	-1	204	0	385	9	445	20	389	11	209
${\tilde{F}}_{s}^{*} (t)$	3	201	8	389	7	449	13	392	14	207
${\tilde{F}}_{l}^{*} (t)$	0	198	6	383	9	446	19	390	13	208
${\tilde{F}}_{π} (t)$	0	205	-2	399	9	463	25	398	14	208

Tableau 5.2
Populations artificielles (taille de population $N = 1 000) .$ BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage de Poisson avec probabilités d’inclusion dans l’échantillon $π_{i}$ proportionnelles aux écarts-types des lois $t$ de Student non centrales avec $ν =5$ dl et avec paramètres de non-centralité $μ =15 x_{i} .$ Taille espérée d’échantillon $n^{*} =100$
Sommaire du tableau
Le tableau montre les résultats de Tableau 5.2
Populations artificielles (taille de population BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage de Poisson avec probabilités d’inclusion dans l’échantillon proportionnelles aux écarts-types des lois de Student non centrales avec dl et avec paramètres de non-centralité Taille espérée d’échantillon
XXXX , XXXX, BIAIS , REQM et REQM , calculées selon XXXX avec XXXX i.i.d. de Student centrale XXXX avec XXXX, XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX, XXXX avec XXXX i.i.d. de Student XXXX avec XXXX, XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX, XXXX avec XXXX i.i.d. de Student XXXX avec XXXX et XXXX avec XXXX indép. de Student non centrale XXXX avec XXXX et XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM	BIAIS	REQM
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student centrale avec $ν =5$
${\hat{F}}_{s} (t)$	-10	252	-11	593	-22	738	-20	743	6	357
${\hat{F}}_{l} (t)$	-1	237	9	543	-15	621	-5	590	11	302
${\hat{F}}_{s}^{*} (t)$	22	244	-29	485	-3	555	9	515	-17	297
${\hat{F}}_{l}^{*} (t)$	14	238	-10	492	-5	564	14	524	-1	283
${\tilde{F}}_{s} (t)$	-6	247	0	579	-27	724	-40	736	3	349
${\tilde{F}}_{l} (t)$	-2	231	11	526	-1	598	-10	566	7	285
${\tilde{F}}_{s}^{*} (t)$	23	248	23	505	-4	562	-27	531	-20	304
${\tilde{F}}_{l}^{*} (t)$	12	240	20	504	1	573	-13	538	-6	287
${\tilde{F}}_{π} (t)$	-6	220	-7	543	-37	741	-44	929	-48	1 058
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	17	164	30	411	4	749	14	590	15	190
${\hat{F}}_{l} (t)$	47	173	19	383	-1	602	57	498	15	187
${\hat{F}}_{s}^{*} (t)$	21	175	-7	378	-89	554	-11	473	3	192
${\hat{F}}_{l}^{*} (t)$	29	152	-3	367	-99	555	27	481	3	184
${\tilde{F}}_{s} (t)$	1	159	10	406	-11	737	-5	579	-2	194
${\tilde{F}}_{l} (t)$	1	158	9	388	-5	586	14	482	-1	192
${\tilde{F}}_{s}^{*} (t)$	14	186	27	409	-3	562	-17	487	-10	200
${\tilde{F}}_{l}^{*} (t)$	3	160	22	399	-11	566	-5	482	-2	193
${\tilde{F}}_{π} (t)$	-3	162	-7	451	-31	738	-29	980	-55	1 067
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student centrale avec $ν =5$
${\hat{F}}_{s} (t)$	8	461	21	561	-12	259	-18	218	-30	164
${\hat{F}}_{l} (t)$	78	429	183	451	2	248	-161	261	-79	189
${\hat{F}}_{s}^{*} (t)$	-69	306	12	340	10	267	15	199	6	143
${\hat{F}}_{l}^{*} (t)$	-59	294	4	302	56	205	15	172	17	124
${\tilde{F}}_{s} (t)$	-25	441	4	560	-10	257	9	219	5	153
${\tilde{F}}_{l} (t)$	-14	372	35	410	-10	262	4	219	5	151
${\tilde{F}}_{s}^{*} (t)$	-31	333	-2	386	-29	294	4	227	-1	161
${\tilde{F}}_{l}^{*} (t)$	-20	339	15	372	-10	259	11	215	4	151
${\tilde{F}}_{π} (t)$	-15	385	3	746	-37	917	-35	1 004	-48	1 070
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	-4	516	30	671	7	453	11	344	6	182
${\hat{F}}_{l} (t)$	63	409	129	539	61	421	9	341	1	180
${\hat{F}}_{s}^{*} (t)$	44	300	-29	433	-45	422	-47	345	12	180
${\hat{F}}_{l}^{*} (t)$	107	314	-41	420	-60	397	-22	323	31	171
${\tilde{F}}_{s} (t)$	-27	502	8	667	-8	450	0	344	-8	185
${\tilde{F}}_{l} (t)$	-10	364	16	510	11	425	-2	345	-7	182
${\tilde{F}}_{s}^{*} (t)$	-6	325	-9	479	-25	447	-14	356	-10	187
${\tilde{F}}_{l}^{*} (t)$	-7	332	-9	489	-5	426	-3	344	-6	182
${\tilde{F}}_{π} (t)$	-16	349	-2	705	-21	886	-42	1 013	-61	1 069
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
${\hat{F}}_{s} (t)$	36	497	47	629	9	418	-11	320	15	191
${\hat{F}}_{l} (t)$	56	393	186	490	43	383	-48	308	13	184
${\hat{F}}_{s}^{*} (t)$	-29	276	-19	383	-18	380	-43	335	-1	204
${\hat{F}}_{l}^{*} (t)$	-29	274	10	355	7	336	-29	290	23	179
${\tilde{F}}_{s} (t)$	-30	475	12	630	4	421	7	317	6	191
${\tilde{F}}_{l} (t)$	-42	336	31	452	11	390	8	312	8	186
${\tilde{F}}_{s}^{*} (t)$	-31	306	5	429	-18	406	-14	344	-8	210
${\tilde{F}}_{l}^{*} (t)$	-28	308	14	424	7	387	5	315	7	191
${\tilde{F}}_{π} (t)$	-15	380	10	739	-23	891	-37	993	-47	1 064
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
${\hat{F}}_{s} (t)$	24	308	69	687	53	690	38	406	2	188
${\hat{F}}_{l} (t)$	47	301	131	553	139	561	91	393	-2	186
${\hat{F}}_{s}^{*} (t)$	15	237	2	435	-135	513	-59	411	12	186
${\hat{F}}_{l}^{*} (t)$	27	235	18	435	-149	506	-5	374	13	179
${\tilde{F}}_{s} (t)$	-28	274	-8	673	4	688	3	403	-10	191
${\tilde{F}}_{l} (t)$	-29	251	-12	512	17	541	7	395	-9	188
${\tilde{F}}_{s}^{*} (t)$	-3	255	-12	481	-7	536	-20	422	-12	196
${\tilde{F}}_{l}^{*} (t)$	-12	251	-16	489	2	538	-4	399	-9	189
${\tilde{F}}_{π} (t)$	-10	267	-8	608	-4	860	-38	1 009	-63	1 066

Tableau 5.3
Populations réelles (taille de population $N =284) .$ BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage aléatoire simple sans remise. Taille d’échantillon $n =30$
Sommaire du tableau

Le tableau montre les résultats de Tableau 5.3
Populations réelles (taille de population XXXX BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage aléatoire simple sans remise. Taille d’échantillon XXXX
BIAIS , REQM , REQM and BIAISR , MU284 Population avec XXXX et XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAIS	REQM	BIAIS	REQM	BIAISR	REQM	BIAIS	REQM	BIAIS	REQM
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln P 85$
${\hat{F}}_{s} (t)$	133	421	339	625	180	529	-265	490	-187	439
${\hat{F}}_{l} (t)$	52	380	67	588	45	555	-63	469	-87	370
${\hat{F}}_{s}^{*} (t)$	8	81	-154	203	90	130	62	123	6	54
${\hat{F}}_{l}^{*} (t)$	28	66	-170	212	69	112	57	109	2	50
${\tilde{F}}_{s} (t)$	-28	300	-24	497	8	483	-48	421	-38	319
${\tilde{F}}_{l} (t)$	-28	326	-96	569	-52	544	3	466	1	319
${\tilde{F}}_{s}^{*} (t)$	26	177	-11	302	0	244	1	308	-18	102
${\tilde{F}}_{l}^{*} (t)$	29	179	-10	302	-2	243	-1	308	-21	104
${\tilde{F}}_{π} (t)$	22	388	-10	771	9	864	5	731	-43	394
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln R E V 84$
${\hat{F}}_{s} (t)$	143	449	303	643	138	554	-217	543	-166	446
${\hat{F}}_{l} (t)$	62	395	62	611	36	582	-49	519	-71	376
${\hat{F}}_{s}^{*} (t)$	-11	204	-32	300	-101	328	42	285	31	155
${\hat{F}}_{l}^{*} (t)$	36	183	-40	288	-149	345	6	261	34	122
${\tilde{F}}_{s} (t)$	5	340	-22	548	4	557	-30	498	-23	332
${\tilde{F}}_{l} (t)$	-2	349	-78	599	-36	588	10	522	8	331
${\tilde{F}}_{s}^{*} (t)$	24	303	7	446	-6	494	2	439	-13	209
${\tilde{F}}_{l}^{*} (t)$	29	304	4	443	-6	495	-1	432	-18	192
${\tilde{F}}_{π} (t)$	34	395	1	766	16	880	9	744	-37	398

Tableau 5.4
Populations réelles (taille de population $N =284) .$ BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage de Poisson avec probabilités d’inclusion proportionnelles à la valeur absolue des résidus de la régression linéaire des valeurs $y_{i}$ de la population sur les valeurs $x_{i}$ de la population. Taille espérée $n^{*} =30$
Sommaire du tableau
Le tableau montre les résultats de Populations réelles (taille de population XXXX BIAIS et REQM des estimateurs de la fonction de répartition sous échantillonnage de Poisson avec probabilités d’inclusion proportionnelles à la valeur absolue des résidus de la régression linéaire des valeurs XXXX de la population sur les valeurs XXXX de la population. Taille espérée XXXX XXXX, BIAIS , REQM , REQM et BIAISR , calculées selon Population MU284 avec XXXX et XXXX unités de mesure (figurant comme en-tête de colonne).
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	BIAIS	REQM	BIAIS	REQM	BIAISR	REQM	BIAIS	REQM	BIAIS	REQM
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln P 85$
${\hat{F}}_{s} (t)$	204	420	485	668	239	519	-412	626	-90	317
${\hat{F}}_{l} (t)$	180	424	417	684	319	614	-239	548	-148	348
${\hat{F}}_{s}^{*} (t)$	-41	97	-118	199	132	178	40	140	-71	104
${\hat{F}}_{l}^{*} (t)$	11	70	-147	211	63	128	-25	122	-85	106
${\tilde{F}}_{s} (t)$	24	360	30	649	0	675	-68	614	58	368
${\tilde{F}}_{l} (t)$	9	390	-63	737	-64	774	-7	682	75	414
${\tilde{F}}_{s}^{*} (t)$	16	184	-14	307	36	283	16	323	-11	103
${\tilde{F}}_{l}^{*} (t)$	25	187	-15	312	30	286	14	328	-11	112
${\tilde{F}}_{π} (t)$	40	445	73	1 983	12	2 498	-43	3 094	-49	3 341
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln R E V 84$
${\hat{F}}_{s} (t)$	349	660	1 185	1 373	890	1 059	458	654	-32	270
${\hat{F}}_{l} (t)$	287	601	1 003	1 236	771	989	484	695	42	263
${\hat{F}}_{s}^{*} (t)$	317	453	739	866	761	879	624	701	159	207
${\hat{F}}_{l}^{*} (t)$	364	471	720	842	718	824	572	647	96	158
${\tilde{F}}_{s} (t)$	35	488	82	818	-31	772	7	634	-8	326
${\tilde{F}}_{l} (t)$	22	500	3	878	-98	852	40	704	27	354
${\tilde{F}}_{s}^{*} (t)$	37	317	32	498	-13	513	32	412	7	157
${\tilde{F}}_{l}^{*} (t)$	51	313	30	498	-30	518	12	411	-10	149
${\tilde{F}}_{π} (t)$	32	671	19	1 658	-172	2 354	-173	2 787	-191	2 935

Considérons enfin les résultats des simulations concernant les estimateurs de variance de la section 4. Les tableaux 5.5 à 5.8 donnent le biais relatif (BIAISR) et la racine carrée de l’erreur quadratique moyenne relative (REQMR) pour chacun d’eux. Par exemple, selon les estimations de variance ${\tilde{V}}_{b} (\tilde{F} (t)),$ $b =1,2, \dots, B,$ obtenues au moyen de l’estimateur $\tilde{V} (\tilde{F} (t)),$

$BIAISR := \frac{1}{B} \sum_{b =1}^{B} \frac{{\tilde{V}}_{b} (\tilde{F} (t)) - V_{B} (\tilde{F} (t))}{V_{B} (\tilde{F} (t))} \times 10 000$

$REQMR := \frac{\sqrt{\frac{1}{B} \sum_{b =1}^{B} {({\tilde{V}}_{b} (\tilde{F} (t)) - V_{B} (\tilde{F} (t)))}^{2}}}{V_{B} (\tilde{F} (t))} \times 10 000$

où

$V_{B} (\tilde{F} (t)) := \frac{1}{B} \sum_{b =1}^{B} {({\tilde{F}}_{b} (t) - F_{N} (t))}^{2} .$

À titre de référence, nous donnons également les BIAISR et REQMR de l’estimateur

$\tilde{V} ({\tilde{F}}_{π} (t)) := \frac{1}{N^{2}} \sum_{i, j \in s} \frac{π_{i, j} - π_{i} π_{j}}{π_{i, j} π_{i} π_{j}} I (y_{i} \leq t) I (y_{j} \leq t)$

pour la variance de l’estimateur de Horvitz-Thompson.

Tableau 5.5
Populations artificielles (taille de population $N = 1 000) .$ BIAISR et REQMR des estimateurs de variance sous échantillonnage aléatoire simple sans remise. Taille d’échantillon $n =100$
Sommaire du tableau
Le tableau montre les résultats de Populations artificielles (taille de population XXXX BIAISR et REQMR des estimateurs de variance sous échantillonnage aléatoire simple sans remise. Taille d’échantillon XXXX XXXX, BIAISR , REQMR et REQMR, calculées selon avec XXXX i.i.d. XXXX de Student centrale avec XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student centrale avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1 092	32 442	-1 249	3 895	-1 714	3 077	-1 536	3 828	-824	34 601
$\tilde{V} ({\tilde{F}}_{l} (t))$	-576	31 726	-603	3 838	-1 122	3 374	-951	3 758	-441	33 055
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 091	32 579	-1 292	3 914	-1 708	3 085	-1 640	3 828	-802	34 809
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-556	31 881	-622	3 857	-1 148	3 361	-1 025	3 749	-425	33 184
$\tilde{V} ({\tilde{F}}_{π} (t))$	42	30 952	57	3 928	-592	3 776	-287	3 825	551	33 462
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1 900	29 622	50	4 707	-917	3 557	-998	3 695	-1 480	29 417
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 359	29 623	535	4 572	-395	3 881	-527	3 736	-1 277	28 267
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 832	30 119	-101	4 710	-991	3 530	-1 077	3 704	-1 398	29 927
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1 362	29 713	465	4 559	-420	3 865	-591	3 718	-1 236	28 489
$\tilde{V} ({\tilde{F}}_{π} (t))$	-351	29 132	1 096	4 215	-78	4 074	574	4 067	-638	29 507
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2 170	11 624	-1 027	2 480	-816	3 274	-1 424	2 583	-1 946	8 681
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 534	11 605	-529	2 632	-148	2 975	-859	2 590	-1 151	9 015
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 765	12 107	-1 108	2 529	-714	3 366	-1 318	2 660	-1 905	8 658
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1 062	11 948	-671	2 735	-212	3 291	-762	2 785	-1 048	8 590
$\tilde{V} ({\tilde{F}}_{π} (t))$	254	31 545	-52	3 726	136	4 152	267	3 992	35	30 264
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1 642	25 809	-855	3 541	-1 076	3 038	-1 081	3 030	-1 361	21 157
$\tilde{V} ({\tilde{F}}_{l} (t))$	-950	25 692	-323	3 509	-597	3 312	-617	3 164	-1 124	20 231
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 385	26 406	-997	3 505	-1 089	3 045	-1 096	3 033	-1 310	21 393
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-832	26 212	-292	3 556	-614	3 317	-716	3 154	-1 135	20 286
$\tilde{V} ({\tilde{F}}_{π} (t))$	105	29 621	507	3 857	209	4 244	425	3 910	-337	29 082
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2 465	30 612	-1 121	4 594	-1 512	3 183	-1 958	3 076	-863	19 720
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 780	28 103	-663	4 420	-1 092	3 319	-1 491	3 140	-439	18 985
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-2 052	33 980	-1 150	4 619	-1 537	3 217	-1 948	3 127	-954	19 637
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1 194	33 573	-691	4 472	-1 124	3 368	-1 438	3 228	-357	19 245
$\tilde{V} ({\tilde{F}}_{π} (t))$	-81	30 001	9	3 756	-110	3 996	-598	3 661	440	32 455
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-1 873	29 437	-758	3 759	-621	3 476	-709	3 599	-1 298	27 679
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 267	28 511	-284	3 661	-131	3 758	-321	3 552	-1 075	26 790
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 710	30 670	-928	3 741	-628	3 510	-777	3 603	-1 245	27 972
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-939	30 486	-270	3 764	-171	3 803	-375	3 581	-1 014	26 926
$\tilde{V} ({\tilde{F}}_{π} (t))$	178	29 640	599	3 816	533	4 324	590	3 874	-404	28 917

Tableau 5.6
Populations artificielles (taille de population $N = 1 000) .$ BIAISR et REQMR des estimateurs de variance sous échantillonnage de Poisson avec probabilités d’inclusion dans l’échantillon $π_{i}$ proportionnelles aux écarts-types des lois $t$ de Student non centrale avec $v = 5$ dl et avec paramètre de non-centralité $μ = 15 x_{i} .$ Taille espérée d’échantillon $n^{*} = 100$
Sommaire du tableau
Le tableau montre les résultats de Populations artificielles (taille de population XXXX BIAISR et REQM des estimateurs de variance sous échantillonnage de Poisson avec probabilités d’inclusion dans l’échantillon XXXX proportionnelles aux écarts-types des lois XXXX de Student non centrale avec XXXX dl et avec paramètre de non-centralité XXXX Taille espérée d’échantillon XXXX. Les données sont présentées selon (titres de rangée) et XXXX, BIAISR , REQM et REQM, calculées selon avec XXXX i.i.d. XXXX de Student centrale avec XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student centrale avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-3 306	65 777	-4 248	8 032	-5 093	4 242	-6 258	4 844	-5 652	32 037
$\tilde{V} ({\tilde{F}}_{l} (t))$	-2 048	47 035	-2 656	4 705	-2 434	3 116	-3 310	3 939	-3 092	29 380
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3 362	36 855	-2 488	4 409	-1 910	3 147	-2 869	3 910	-4 329	23 247
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-2 696	39 509	-2 076	4 450	-1 768	3 163	-2 648	3 811	-3 244	26 343
$\tilde{V} ({\tilde{F}}_{π} (t))$	113	129 637	259	15 120	618	6 327	193	5 429	273	6 097
	$y_{i} = ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-740	125 975	-2 522	14 864	-5 466	3 658	-4 896	6 691	-1 551	83 262
$\tilde{V} ({\tilde{F}}_{l} (t))$	-391	83 047	-1 503	8 946	-2 428	4 099	-2 228	5 526	-1 154	54 680
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3 260	58 072	-2 649	7 661	-2 260	3 936	-2 795	5 011	-2 116	48 739
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-716	77 935	-2 000	7 979	-1 934	4 235	-2 279	5 243	-1 243	52 531
$\tilde{V} ({\tilde{F}}_{π} (t))$	666	251 134	-564	26 553	-87	7 344	-2	6 029	407	6 610
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-6 801	7 898	-6 470	4 281	-1 059	22 596	-398	32 401	-1 650	72 632
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4 978	5 826	-2 898	4 473	-603	9 530	206	15 226	-1 157	40 466
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4 520	6 691	-2 710	4 213	-3 245	6 723	-1 156	12 681	-2 458	32 907
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-4 226	6 206	-1 674	5 062	-978	7 874	55	12 781	-1 283	33 737
$\tilde{V} ({\tilde{F}}_{π} (t))$	-707	47 550	118	7 214	609	4 409	743	4 628	435	4 800
	$y_{i} =10 x_{i} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-7 398	8 847	-6 235	3 667	-2 493	8 171	-1 051	16 299	-1 440	71 943
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4 548	9 463	-3 136	3 282	-1 187	4 246	-832	7 638	-982	45 182
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-3 902	11 727	-2 808	3 409	-2 411	3 501	-1 721	6 737	-1 671	41 389
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-3 598	10 771	-2 610	3 462	-1 284	3 988	-852	7 008	-972	43 017
$\tilde{V} ({\tilde{F}}_{π} (t))$	146	57 044	-42	8 708	520	4 784	214	4 686	390	5 085
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ i.i.d. $t$ de Student avec $ν =5$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-7 731	8 568	-6 597	3 484	-2 442	7 775	-903	16 067	-1 967	56 480
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4 611	9 378	-2 990	3 252	-874	4 119	-347	7 420	-1 310	35 051
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4 747	11 909	-2 679	3 298	-1 896	3 272	-2 248	5 747	-3 382	27 222
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-4 223	10 380	-2 100	3 494	-788	3 731	-550	5 975	-1 795	29 856
$\tilde{V} ({\tilde{F}}_{π} (t))$	-428	47 038	-206	7 350	641	4 504	738	4 708	487	4 943
	$y_{i} =10 x_{i}^{1 / 4} + ε_{i},$ avec $ε_{i} \sim$ indép. $t$ de Student non centrale avec $ν =5$ et $μ =15 x_{i}$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-4 936	40 696	-6 111	4 579	-5 549	4 035	-1 864	14 381	-1 509	84 892
$\tilde{V} ({\tilde{F}}_{l} (t))$	-3 004	29 404	-2 764	3 962	-2 436	3 606	-1 234	7 357	-1 103	53 875
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-4 328	27 704	-2 516	4 235	-2 671	3 332	-2 586	5 955	-1 939	47 601
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-3 454	28 267	-2 263	4 160	-2 329	3 574	-1 433	6 682	-1 171	50 985
$\tilde{V} ({\tilde{F}}_{π} (t))$	152	98 607	663	12 879	15	5 376	20	5 080	429	5 619

Tableau 5.7
Populations réelles (taille de population $N = 284) .$ BIAISR et REQMR des estimateurs de variance sous échantillonnage aléatoire simple sans remise. Taille d’échantillon $n = 30$
Sommaire du tableau
Le tableau montre les résultats de Populations réelles (taille de population XXXX BIAISR et REQM des estimateurs de variance sous échantillonnage aléatoire simple sans remise. Taille d’échantillon XXXX XXXX, BIAISR , REQM et REQM, calculées selon Population MU284 avec XXXX et XXXX et Population MU284 avec XXXX et XXXX unités de mesure (figurant comme en-tête de colonne).
	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln P 85$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2 853	16 809	-1 700	3 037	-1 554	2 984	-1 100	4 633	-5 503	16 257
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 110	16 374	-1 827	2 760	-1 683	2 847	-927	4 387	-3 016	18 685
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 043	19 081	-91	7 728	-448	9 120	-484	7 715	-1 877	65 298
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-424	18 971	104	7 819	-382	9 110	-301	7 799	-1 058	62 968
$\tilde{V} ({\tilde{F}}_{π} (t))$	-186	29 720	-603	3 901	31	3 971	500	4 383	-74	28 418
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln R E V 84$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-2 283	16 303	-1 450	3 538	-945	3 526	-1 071	4 300	-4 832	19 401
$\tilde{V} ({\tilde{F}}_{l} (t))$	-1 095	16 755	-1 427	3 181	-938	3 390	-780	4 051	-2 753	20 551
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-1 737	14 642	-298	5 648	-546	5 282	-736	5 679	-3 564	38 344
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1 174	14 111	-27	5 856	-422	5 452	-228	5 974	-1 433	43 923
$\tilde{V} ({\tilde{F}}_{π} (t))$	-307	28 421	-460	3 963	-344	3 850	112	4 235	-401	27 987

Tableau 5.8
Populations réelles (taille de population $N = 284) .$ BIAISR et REQMR des estimateurs de variance sous échantillonnage de Poisson avec probabilités d’inclusion proportionnelles à la valeur absolue des résidus de la régression linéaire des valeurs $y_{i}$ de la population sur les valeurs $x_{i}$ de la population. Taille espérée $n^{*} = 30$
Table summary
This table displays the results of Real populations (population size XXXX RBIAS and RRMSE of variance estimators under Poisson sampling with inclusion probabilities proportional to the absolute value of the residuals of the linear regression of the population XXXX values on the population XXXX values. Expected size XXXX XXXX, RBIAS , RRMSE and RRMSE, calculated using MU284 population with XXXX and XXXX and MU284 population with XXXX and XXXX units of measure (appearing as column headers).
	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR	BIAISR	REQMR
	$t = F_{N}^{- 1} (0,05)$		$t = F_{N}^{- 1} (0,25)$		$t = F_{N}^{- 1} (0,50)$		$t = F_{N}^{- 1} (0,75)$		$t = F_{N}^{- 1} (0,95)$
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln P 85$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-3 502	26 342	-1 841	14 037	-2 691	12 087	-3 415	9 674	-5 932	26 823
$\tilde{V} ({\tilde{F}}_{l} (t))$	-2 159	27 610	-1 782	14 010	-2 840	12 002	-3 186	10 177	-4 455	26 802
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-434	22 455	515	15 503	-506	31 296	-1 460	23 496	-2 649	78 527
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-80	22 921	677	15 575	-280	33 294	-1 283	26 612	-1 597	72 166
$\tilde{V} ({\tilde{F}}_{π} (t))$	-294	361 991	522	75 891	43	48 764	-241	36 354	90	32 354
	Population MU284 avec $Y = \ln R M T 85$ et $X = \ln R E V 84$
$\tilde{V} ({\tilde{F}}_{s} (t))$	-5 220	18 699	-3 667	8 749	-3 222	7 537	-3 018	9 279	-4 955	44 597
$\tilde{V} ({\tilde{F}}_{l} (t))$	-4 254	20 765	-3 100	9 180	-3 435	7 231	-3 196	8 540	-3 461	43 206
$\tilde{V} ({\tilde{F}}_{s}^{*} (t))$	-2 938	18 922	-1 110	11 828	-1 265	8 726	-1 040	10 963	-3 682	89 262
$\tilde{V} ({\tilde{F}}_{l}^{*} (t))$	-1 938	19 997	-699	12 641	-1 003	9 305	-599	11 545	-1 558	98 798
$\tilde{V} ({\tilde{F}}_{π} (t))$	-143	128 401	493	33 934	-255	18 473	-91	17 904	327	16 463

Comme le montrent les résultats des simulations, les estimateurs de variance souffrent d’une grande variabilité. Ce problème touche aussi l’estimateur de variance pour l’estimateur de Horvitz-Thompson qui, à l’occasion, présente de très grandes REQMR. Il est en outre intéressant de noter que, si le BIAISR des estimateurs de variance pour les estimateurs par la différence généralisée est presque toujours négatif et parfois assez grand en valeur absolue, celui de l’estimateur de variance pour l’estimateur de Horvitz-Thompson est positif dans la plupart des cas considérés.

Remerciements

La présente étude a été financée en partie par la subvention FAR 2014-ATE-0200 octroyée par University of Milano-Bicocca.

Annexe

Soit $β$ une suite de nombres réels. Tout au long de la présente annexe, nous désignerons par $O_{i_{1}, i_{2}, \dots, i_{k}} (β)$ les termes de reste qui peuvent dépendre de $x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}$ et qui sont de même ordre que la suite $β$ uniformément pour $i_{1}, i_{2}, \dots, i_{k} \in U .$ Formellement, $R (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}) = O_{i_{1}, i_{2}, \dots, i_{k}} (β)$ si

$\sup_{i_{1}, i_{2}, \dots, i_{k} \in U} | R (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{k}}) | = O (β) .$

En outre, pour simplifier la notation, nous écrirons $m_{i}$ à la place de $m (x_{i})$ et $σ_{i}^{2}$ à la place de $σ^{2} (x_{i}) .$

Biais de l’estimateur fondé sur le modèle de Kuo

$\begin{array}{l} E (\hat{F} (t) - F_{N} (t)) & = E (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})]) \\ = \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{j} | x_{j}) - G (t - m_{i} | x_{i})] \\ = \frac{1}{2 N} \sum_{i \notin s} [G^{(2,0)} (t - m_{i} | x_{i}) {(m_{i'})}^{2} - G^{(1,0)} (t - m_{i} | x_{i}) m_{i''} \\ - 2 G^{(1,1)} (t - m_{i} | x_{i}) m_{i'} + G^{(0, 2)} (t - m_{i} | x_{i})] \sum_{j \in s} w_{i, j} {(x_{j} - x_{i})}^{2} + o (λ^{2}) \\ = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{2 μ_{0}} \int_{a}^{b} [G^{(2,0)} (t - m (x) | x) {(m^{'} (x))}^{2} - G^{(1,0)} (t - m (x) | x) m^{''} (x) \\ - 2 G^{(1,1)} (t - m (x) | x) m^{'} (x) + G^{(0, 2)} (t - m (x) | x)] h_{\bar{s}} (x) d x + o (λ^{2}) . \end{array}$

Biais de l’estimateur par la différence généralisée de Kuo

Écrivons

$\begin{array}{l} \tilde{F} (t) - F_{N} (t) & = \frac{1}{N} {\sum_{i \notin s} \sum_{j \in s} {\tilde{w}}_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})] \\ + \sum_{i \in s} (1 - \frac{1}{π_{i}}) \sum_{j \in s} {\tilde{w}}_{i, j} [I (ε_{j} \leq t - m_{j}) - I (ε_{i} \leq t - m_{i})]} . \end{array}$

Des étapes similaires à celles suivies pour $\hat{F} (t)$ montrent que

$\begin{array}{l} E (\tilde{F} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{2 μ_{0}} \int_{a}^{b} [G^{(2,0)} (t - m (x) | x) {(m^{'} (x))}^{2} - G^{(1,0)} (t - m (x) | x) m^{''} (x) \\ - 2 G^{(1,1)} (t - m (x) | x) m^{'} (x) + G^{(0, 2)} (t - m (x) | x)] h (x) d x + o (λ^{2}), \end{array}$

où

$h (x) := h_{\bar{s}} (x) + (1 - π^{- 1} (x)) h_{s} (x) .$

Variance de l’estimateur fondé sur le modèle de Kuo

$\begin{array}{l} var (\hat{F} (t) - F_{N} (t)) & = var (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} I (ε_{j} \leq t - m_{j}) - \frac{1}{N} \sum_{i \notin s} I (y_{i} \leq t)) \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] \\ + \frac{1}{N^{2}} \sum_{i \notin s} [G (t - m_{i} | x_{i}) - G^{2} (t - m_{i} | x_{i})] \\ = A_{1} + A_{2}, \end{array}$

où

$\begin{array}{l} A_{1} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {(\sum_{i \notin s} w_{i, j})}^{2} \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α) \end{array}$

$\begin{array}{l} A_{2} & := \frac{1}{N^{2}} \sum_{i \notin s} [G (t - m_{i} | x_{i}) - G^{2} (t - m_{i} | x_{i})] \\ = \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + O (n^{- 1} α) . \end{array}$

Donc,

$\begin{array}{l} var (\hat{F} (t) - F_{N} (t)) & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + O ({(n λ)}^{- 1} α) . \end{array}$

Variance de l’estimateur par la différence généralisée de Kuo

Notons que,

$\tilde{F} (t) - F_{N} (t) = \frac{1}{N} {\sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1) + (π_{j}^{- 1} - 1)] - \sum_{i \notin s} I (y_{i} \leq t)}$

de sorte que

$\begin{array}{l} var (\tilde{F} (t) - F_{N} (t)) & = var (\frac{1}{N} \sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]) \\ + var (\frac{1}{N} \sum_{i \notin s} I (y_{i} \leq t)) \\ = B_{1} + A_{2}, \end{array}$

où le terme $A_{2}$ est le même que dans la variance de $\hat{F} (t),$ et où

$\begin{array}{l} B_{1} & := var (\frac{1}{N} \sum_{j \in s} I (y_{j} \leq t) [\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]) \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {[\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) - \sum_{i \in s} {\tilde{w}}_{i, j} (π_{i}^{- 1} - 1)]}^{2} \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {[\sum_{i \notin s} {\tilde{w}}_{i, j} + (π_{j}^{- 1} - 1) (1 - \sum_{i \in s} {\tilde{w}}_{i, j})]}^{2} + O (λ n^{- 1}) \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α + λ n^{- 1}) \\ = A_{1} + O ({(n λ)}^{- 1} α + λ n^{- 1}) . \end{array}$

Donc,

$var (\tilde{F} (t) - F_{N} (t)) = var (\hat{F} (t) - F_{N} (t)) + O ({(n λ)}^{- 1} α + λ n^{- 1}) .$

Biais de l’estimateur fondé sur le modèle avec valeurs prédites modifiées

Soit ${\hat{\hat{m}}}_{i} := \sum_{k \in s} w_{i, k} m_{k},$ $c_{i, j} :=1 - w_{j, j} + w_{i, j}$ et

$d_{i, j} := \frac{1}{c_{i, j}} [(1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + \sum_{k \in s, k \neq j} (w_{j, k} - w_{i, k}) ε_{k}] .$

Observons que $w_{i, j} = O_{i, j} ({(n λ)}^{- 1})$ d’où

$y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i}$

est (asymptotiquement, aussitôt que $c_{i, j} >0)$ équivalent à

$ε_{j} \leq t - m_{i} + d_{i, j} .$

Comme $d_{i, j}$ ne dépend pas de $ε_{j},$ il s’ensuit que

$\begin{array}{l} E (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i})) & = E (I (ε_{j} \leq t - m_{i} + d_{i, j})) \\ = E (E (I (ε_{j} \leq t - m_{i} + d_{i, j}) | ε_{k}, k \neq j)) \\ = E (G (t - m_{i} + d_{i, j} | x_{j})) . \end{array} (A .1)$

Or, en utilisant le fait que

$d_{i, j} = (1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + \sum_{k \in s, k \neq j} (w_{j, k} - w_{i, k}) ε_{k} + R (d_{i, j}), (A .2)$

où

$E^{1 / 4} ({| R (d_{i, j}) |}^{4}) = O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}), (A .3)$

on voit en examinant (A.1) que

$\begin{array}{l} E (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i})) & = E (G (t - m_{i} + d_{i, j}) | x_{j}) \\ = G (t - m_{i} | x_{j}) + G^{(1,0)} (t - m_{i} | x_{j}) E (d_{i, j}) \\ + \frac{1}{2} G^{(2,0)} (t - m_{i} | x_{j}) E (d_{i, j}^{2}) + o_{i, j} (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .4)$

Donc,

$\begin{array}{l} E ({\hat{F}}^{*} (t) - F_{N} (t)) & = E (\frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} (I (y_{j} - {\hat{m}}_{j} \leq t - {\hat{m}}_{i}) - I (y_{i} \leq t))) \\ = \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{i} | x_{j}) - G (t - m_{i} | x_{i})] \\ + \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) E (d_{i, j}) \\ + \frac{1}{2 N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(2, 0)} (t - m_{i} | x_{j}) E (d_{i, j}^{2}) + o (λ^{4} + {(n λ)}^{- 1}) \\ := C_{1} + C_{2} + C_{3} + o (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .5)$

Considérons d’abord $C_{1}$ et notons que

$\begin{array}{l} C_{1} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} [G (t - m_{i} | x_{j}) - G (t - m_{i} | x_{i})] \\ = \frac{1}{2 N} \sum_{i \notin s} G^{(0, 2)} (t - m_{i} | x_{i}) \sum_{j \in s} w_{i, j} {(x_{j} - x_{i})}^{2} + o (λ^{2}) \\ = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h_{\bar{s}} (x) d x + o (λ^{2}) . \end{array}$

Considérons ensuite $C_{2} .$ (A.2) et (A.3) impliquent que

$\begin{array}{l} E (d_{i, j}) & = (1 - c_{i, j}) (t - m_{i}) + ({\hat{\hat{m}}}_{j} - m_{j}) - ({\hat{\hat{m}}}_{i} - m_{i}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \\ = (w_{j, j} - w_{i, j}) (t - m_{i}) + m_{j''} \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - m_{i''} \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2} \\ + o_{i, j} (λ^{2}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \\ = (w_{j, j} - w_{i, j}) (t - m_{i}) + (m_{j''} - m_{i''}) \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} \\ + m_{i''} (\sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) \\ + o_{i, j} (λ^{2}) + O_{i, j} (λ n^{- 1} + {(n λ)}^{- 3 / 2}) \end{array}$

de sorte que

$C_{2} = C_{2, a} + C_{2, b} + C_{2, c} + o (λ^{2}) + O (λ n^{- 1} + {(n λ)}^{- 3 / 2}),$

où

$\begin{array}{l} C_{2, a} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) (w_{j, j} - w_{i, j}) (t - m_{i}) \\ = \frac{1}{N} \sum_{i \notin s} G^{(1, 0)} (t - m_{i} | x_{i}) (t - m_{i}) \sum_{j \in s} w_{i, j} (w_{j, j} - w_{i, j}) + O (n^{- 1}) \\ = \frac{1}{n λ} \frac{N - n}{N} \frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) [h_{\bar{s}} (x) / h_{s} (x)] d x \\ + O ({(n λ)}^{- 1} λ^{- 1} α + n^{- 1}) \end{array}$

avec $κ := \int_{- 1}^{1} K^{2} (u) d u,$

$\begin{array}{l} C_{2, b} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) (m_{j''} - m_{i''}) \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} \\ = o (λ^{2}) \end{array}$

$\begin{array}{l} C_{2, c} & := \frac{1}{N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(1, 0)} (t - m_{i} | x_{j}) m_{i''} (\sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) \\ = \frac{1}{N} \sum_{i \notin s} G^{(1, 0)} (t - m_{i} | x_{i}) m_{i''} (\sum_{j \in s} w_{i, j} \sum_{k \in s} w_{j, k} {(x_{k} - x_{j})}^{2} - \sum_{k \in s} w_{i, k} {(x_{k} - x_{i})}^{2}) + o (λ^{2}) \\ = o (λ^{2}) . \end{array}$

Considérons enfin $C_{3} .$ Notons que, d’après (A.2) et (A.3),

$E (d_{i, j}^{2}) = \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} σ_{k}^{2} + O_{i, j} (λ^{4} + {(n λ)}^{- 2}) (A .6)$

d’où

$\begin{array}{l} C_{3} & = \frac{1}{2 N} \sum_{i \notin s} \sum_{j \in s} w_{i, j} G^{(2, 0)} (t - m_{i} | x_{j}) \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} σ_{k}^{2} + O (λ^{4} + {(n λ)}^{- 2}) \\ = \frac{1}{2 N} \sum_{i \notin s} G^{(2, 0)} (t - m_{i} | x_{i}) σ_{i}^{2} \sum_{j \in s} w_{i, j} \sum_{k \in s} {(w_{j, k} - w_{i, k})}^{2} + o ({(n λ)}^{- 1}) + O (λ^{4}) \\ = \frac{1}{n λ} \frac{N - n}{N} \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) [h_{\bar{s}} (x) / h_{s} (x)] d x + o ({(n λ)}^{- 1}) + O (λ^{4}) \end{array}$

avec $θ := \int_{- 1}^{1} K (v) \int_{- 1}^{1} K (u + v) K (u) d u d v .$

En substituant les développements susmentionnés à $C_{1}, C_{2}$ et $C_{3}$ dans (A.5), on obtient finalement

$\begin{array}{l} E ({\hat{F}}^{*} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h_{\bar{s}} (x) d x \\ + \frac{1}{n λ} \frac{N - n}{N} [\frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) h_{s}^{- 1} (x) h_{\bar{s}} (x) d x \\ + \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) h_{s}^{- 1} (x) h_{\bar{s}} (x) d x] \\ + o (λ^{2} + {(n λ)}^{- 1}) . \end{array}$

Biais de l’estimateur par la différence généralisée avec valeurs prédites modifiées

Soit ${\tilde{d}}_{i, j}$ l’équivalent pondéré selon le plan de sondage de $d_{i, j}$ et observons que

$\begin{array}{l} {\tilde{F}}^{*} (t) - F_{N} (t) & = \frac{1}{N} [\sum_{i \notin s} \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t)) \\ + \sum_{i \in s} (1 - π_{i}^{- 1}) \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t))] . \end{array} (A .7)$

En adaptant la preuve qui mène à (A.4), on voit que le développement asymptotique en (A.4) est également vérifié en prenant ${\tilde{d}}_{i, j}$ à la place de $d_{i, j} .$ L’adaptation de la partie restante de la preuve mène en bout de ligne à

$\begin{array}{l} E ({\tilde{F}}^{*} (t) - F_{N} (t)) & = λ^{2} \frac{N - n}{N} \frac{μ_{2}}{μ_{0}} \int_{a}^{b} G^{(0, 2)} (t - m (x) | x) h (x) d x \\ + \frac{1}{n λ} \frac{N - n}{N} [\frac{K (0) - κ}{μ_{0}} \int_{a}^{b} G^{(1, 0)} (t - m (x) | x) (t - m (x)) h_{s}^{- 1} (x) h (x) d x \\ + \frac{κ - θ}{μ_{0}^{2}} \int_{a}^{b} G^{(2, 0)} (t - m (x) | x) σ^{2} (x) h_{s}^{- 1} (x) h (x) d x] \\ + o (λ^{2} + {(n λ)}^{- 1}), \end{array}$

où

$h (x) := h_{\bar{s}} (x) + (1 - π^{- 1} (x)) h_{s} (x) .$

Variance de l’estimateur fondé sur le modèle avec valeurs prédites modifiées

Écrivons

${\hat{F}}^{*} (t) - F_{N} (t) = \frac{1}{N} (\sum_{i \notin s} \sum_{j \in s} w_{i, j} I (ε_{j} \leq t - m_{i} + d_{i, j}) - \sum_{i \notin s} I (ε_{i} \leq t - m_{i}))$

et observons que

$var ({\hat{F}}^{*} (t) - F_{N} (t)) = D_{1} + D_{2} + D_{3},$

où

$D_{1} := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})),$

$D_{2} := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} \times cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}}))$

et où $D_{3} := A_{2}$ provenant de la variance de l’estimateur fondé sur le modèle de Kuo.

Considérons $D_{1} .$ Observons que

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})) & = E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) \\ - E (G (t - m_{i_{1}} + d_{i_{1}, j} | x_{j})) E (G (t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) . \end{array} (A .8)$

Puisque

$| (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j}) - (t - m_{i_{1}} \land t - m_{i_{2}}) | \leq | d_{i_{1}, j} | + | d_{i_{2}, j} |,$

il découle de (A.6) que

$E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) = G (t - m_{i_{1}} \land t - m_{i_{2}} | x_{j}) + O_{i_{1}, i_{2}, j} (λ^{2} + {(n λ)}^{- 1 / 2}) . (A .9)$

En outre, de (A.1), (A.4) et (A.6), il découle que

$\begin{array}{l} E (G (t - m_{i} + d_{i, j} | x_{j})) = & G (t - m_{i} | x_{j}) + O_{i, j} (λ^{2} + {(n λ)}^{- 1 / 2}) . \end{array} (A .10)$

En utilisant (A.9) et (A.10) pour obtenir un développement asymptotique pour la covariance en (A.8) et en introduisant par substitution le résultat dans la définition de $D_{1},$ on obtient

$\begin{array}{l} D_{1} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} cov (I (ε_{j} \leq t - m_{i_{1}} + d_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + d_{i_{2}, j})) \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [E (G (t - m_{i_{1}} + d_{i_{1}, j} \land t - m_{i_{2}} + d_{i_{2}, j} | x_{j})) \\ - E (G (t - m_{i_{1}} + d_{i_{1}, j} | x_{j})) E (G (t - m_{i_{2}} + d_{i_{2}, j} | x_{j}))] \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j \in s} w_{i_{1}, j} w_{i_{2}, j} [G (t - m_{i_{1}} \land t - m_{i_{2}} | x_{j}) - G (t - m_{i_{1}} | x_{j}) G (t - m_{i_{2}} | x_{j})] \\ + O (λ^{2} n^{- 1} + {(n λ)}^{- 1 / 2} n^{- 1}) \\ = \frac{1}{N^{2}} \sum_{j \in s} [G (t - m_{j} | x_{j}) - G^{2} (t - m_{j} | x_{j})] {(\sum_{i \notin s} w_{i, j})}^{2} + O (λ n^{- 1} + {(n λ)}^{- 1 / 2} n^{- 1}) \\ = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + O ({(n λ)}^{- 1} α + n^{- 1} λ + n^{- 1} {(n λ)}^{- 1 / 2}) . \end{array} (A .11)$

Considérons ensuite

Puisque

$cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) =0$

si $| x_{i_{1}} - x_{i_{2}} | >2 λ,$ il s’ensuit que les termes de reste $R_{i_{1}, j_{1}, i_{2}, j_{2}},$ dont la contribution à la covariance susmentionnée est d’ordre $O_{i_{1}, j_{1}, i_{2}, j_{2}} (β)$ pour une suite $β$ qui tend vers zéro, apportent à $D_{2}$ un terme d’ordre $O (λ β) .$ Or, soit

$b_{i, j_{1}, j_{2}} := c_{i, j_{1}}^{- 1} (w_{j_{1}, j_{2}} - w_{i, j_{2}}),$

$a_{i, j_{1}, j_{2}} := t - m_{i} + d_{i, j_{1}} - b_{i, j_{1}, j_{2}} ε_{j_{2}}$

et notons que

$t - m_{i} + d_{i, j_{1}} = a_{i, j_{1}, j_{2}} + b_{i, j_{1}, j_{2}} ε_{j_{2}} .$

Puisque $a_{i, j_{1}, j_{2}}$ ne dépend pas de $ε_{j_{1}}$ ni de $ε_{j_{2}},$ il s’ensuit que

$\begin{array}{l} E (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}) I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) \\ = E (E (I (ε_{j_{1}} \leq a_{i_{1}, j_{1}, j_{2}} + b_{i_{1}, j_{1}, j_{2}} ε_{j_{2}}) I (ε_{j_{2}} \leq a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε_{j_{1}}) | ε_{k}, k \neq j_{1}, j_{2})) \\ = E (\int_{- \infty}^{ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}} G (a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε | x_{j_{2}}) d G (ε | x_{j_{1}})) \\ + E (\int_{- \infty}^{ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*}} G (a_{i_{1}, j_{1}, j_{2}} + b_{i_{1}, j_{1}, j_{2}} ε | x_{j_{1}}) d G (ε | x_{j_{2}})) \\ - E (G (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} | x_{j_{1}}) G (ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*} | x_{j_{2}})), \end{array} (A .12)$

où

$ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} := \frac{a_{i_{1,} j_{1}, j_{2}} + a_{i_{2}, j_{2}, j_{1}} b_{i_{1}, j_{1}, j_{2}}}{1 - b_{i_{1}, j_{1}, j_{2}} b_{i_{2}, j_{2}, j_{1}}} .$

Notons que les deux espérances aux troisième et quatrième lignes de (A.12) sont les mêmes si $i_{1}$ et $j_{1}$ sont remplacés par $i_{2}$ et $j_{2},$ respectivement. Donc, il suffit d’analyser la première espérance. Étant donné que

$ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} = t - m_{i_{1}} + d_{i_{1}, j_{1}} + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}} - ε_{j_{2}}) + R (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}),$

où

$E^{1 / 4} ({| R (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}) |}^{4}) = O_{i_{1}, i_{2}, j_{1}, j_{2}} (λ n^{- 1} + {(n λ)}^{- 3 / 2}),$

on voit que

$\begin{array}{l} E (\int_{- \infty}^{ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*}} G (a_{i_{2}, j_{2}, j_{1}} + b_{i_{2}, j_{2}, j_{1}} ε | x_{j_{2}}) d G (ε | x_{j_{1}})) \\ = G (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) [E (d_{i_{1}, j_{1}}) + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}})] \\ + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}) + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) b_{i_{2}, j_{2}, j_{1}} \int_{- \infty}^{t - m_{i_{1}}} ε d G (ε | x_{j_{1}}) \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}}^{2}) + \frac{1}{2} G^{(2, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}^{2}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}} d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}), \end{array} (A .13)$

et que

$\begin{array}{l} E (G (ε_{i_{1}, i_{2}, j_{1}, j_{2}}^{*} | x_{j_{1}}) G (ε_{i_{2}, i_{1}, j_{2}, j_{1}}^{*} | x_{j_{2}})) \\ = G (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) [E (d_{i_{1}, j_{1}}) + b_{i_{1}, j_{1}, j_{2}} (t - m_{i_{2}})] \\ + G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) [E (d_{i_{2}, j_{2}}) + b_{i_{2}, j_{2}, j_{1}} (t - m_{i_{1}})] \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{1}} | x_{j_{1}}) G (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}}^{2}) \\ + \frac{1}{2} G^{(2, 0)} (t - m_{i_{2}} | x_{j_{2}}) G (t - m_{i_{1}} | x_{j_{1}}) E (d_{i_{2}, j_{2}}^{2}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) E (d_{i_{1}, j_{1}} d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}) . \end{array} (A .14)$

En utilisant les développements asymptotiques en (A.4), (A.13) et (A.14), on obtient

$\begin{array}{l} cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + d_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + d_{i_{2}, j_{2}})) \\ = G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) b_{i_{2}, j_{2}, j_{1}} γ_{i_{1}, j_{1}} + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) b_{i_{1}, j_{1}, j_{2}} γ_{i_{2}, j_{2}} \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) cov (d_{i_{1}, j_{1}}, d_{i_{2}, j_{2}}) \\ + o_{i_{1}, i_{2}, j_{1}, j_{2}} (λ^{4} + {(n λ)}^{- 1}), \end{array} (A .15)$

où

$γ_{i, j} := \int_{- \infty}^{t - m_{i}} ε d G (ε | x_{j}) .$

Observons maintenant que

$b_{i, j_{1}, j_{2}} = w_{j_{1}, j_{2}} - w_{i, j_{2}} + O_{i, j_{1}, j_{2}} ({(n λ)}^{- 2})$

et que

$\begin{array}{l} cov (d_{i_{1}, j_{1}}, d_{i_{2}, j_{2}}) & = \frac{1}{c_{i_{1}, j_{1}} c_{i_{2}, j_{2}}} \sum_{k \in s; k \neq j_{1}, j_{2}} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} \\ = \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} + O_{i_{1}, i_{2}, j_{1}, j_{2}} ({(n λ)}^{- 2}) \end{array}$

de sorte que

$D_{2} =2 D_{2 a} + D_{2 b} + o (λ^{5} + n^{- 1}), (A .16)$

où

$\begin{array}{l} D_{2 a} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) (w_{j_{1}, j_{2}} - w_{i_{1}, j_{2}}) γ_{i_{2}, j_{2}} \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) (w_{j_{1}, j_{2}} - w_{i_{1}, j_{2}}) γ_{i_{2}, j_{2}} + O (n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{j_{2} \in s} G^{(1, 0)} (t - m_{j_{2}} | x_{j_{2}}) γ_{j_{2}, j_{2}} [\sum_{j_{1} \in s} w_{j_{1}, j_{2}} \sum_{i_{1} \notin s} w_{i_{1}, j_{1}} \sum_{i_{2} \notin s} w_{i_{2}, j_{2}} - {(\sum_{i \notin s} w_{i, j_{2}})}^{2}] \\ + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = O ({(n λ)}^{- 1} α + n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \end{array} (A .17)$

$\begin{array}{l} D_{2 b} & := \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) \\ \times \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} \\ = \frac{1}{N^{2}} \sum_{i_{1} \notin s} \sum_{i_{2} \notin s} \sum_{j_{1} \in s} \sum_{j_{2} \in s} w_{i_{1}, j_{1}} w_{i_{2}, j_{2}} G^{(1, 0)} (t - m_{i_{1}} | x_{j_{1}}) G^{(1, 0)} (t - m_{i_{2}} | x_{j_{2}}) \\ \times \sum_{k \in s} (w_{j_{1}, k} - w_{i_{1}, k}) (w_{j_{2}, k} - w_{i_{2}, k}) σ_{k}^{2} + O (n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{k \in s} σ_{k}^{2} {[G^{(1, 0)} (t - m_{k} | x_{k})]}^{2} {(\sum_{i \notin s} \sum_{j \in s} w_{i, j} (w_{j, k} - w_{i, k}))}^{2} + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = \frac{1}{N^{2}} \sum_{k \in s} σ_{k}^{2} {[G^{(1, 0)} (t - m_{k} | x_{k})]}^{2} {(\sum_{j \in s} w_{j, k} \sum_{i \notin s} w_{i, j} - \sum_{i \notin s} w_{i, k})}^{2} + O (n^{- 1} λ + n^{- 1} {(n λ)}^{- 1}) \\ = O ({(n λ)}^{- 1} α + n^{- 1} λ) . \end{array} (A .18)$

En regroupant tout, on obtient finalement

$\begin{array}{l} var ({\hat{F}}^{*} (t) - F_{N} (t)) & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] [h_{\bar{s}} (x) / h_{s} (x)] h_{\bar{s}} (x) d x \\ + \frac{1}{N - n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] h_{\bar{s}} (x) d x + o (λ^{5} + n^{- 1}) . \end{array}$

Variance de l’estimateur par la différence généralisée avec valeurs prédites modifiées

Étant donné (A.7), nous allons montrer que

$var ({\tilde{F}}^{*} (t) - F_{N} (t)) = var ({\hat{F}}^{*} (t) - F_{N} (t)) + o (n^{- 1}) (A .19)$

en démontrant que

$var (\frac{1}{N} \sum_{i \in s} (1 - π_{i}^{- 1}) \sum_{j \in s} {\tilde{w}}_{i, j} (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}) - I (y_{i} \leq t))) = o (n^{- 1}) . (A .20)$

Pour prouver (A.20), observons que la variance dans le premier membre peut s’écrire

$E_{1} + E_{2} + E_{3} - 2 E_{4} - 2 E_{5},$

où

$E_{1} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j \in s} {\tilde{w}}_{i_{1}, j} {\tilde{w}}_{i_{2}, j} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{j} \leq t - m_{i_{2}} + {\tilde{d}}_{i_{2}, j})),$

$E_{2} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j_{1} \in s} \sum_{j_{2} \in s, j_{2} \neq j_{1}} {\tilde{w}}_{i_{1}, j} {\tilde{w}}_{i_{2}, j_{2}} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j_{1}} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j_{1}}), I (ε_{j_{2}} \leq t - m_{i_{2}} + {\tilde{d}}_{i_{2}, j_{2}})),$

$\begin{array}{l} E_{3} & := \frac{1}{N^{2}} \sum_{i \in s} {(1 - π_{i}^{- 1})}^{2} var (I (ε_{i} \leq t - m_{i})), \end{array}$

$\begin{array}{l} E_{4} & := \frac{1}{N^{2}} \sum_{i \in s} \sum_{j \in s} {\tilde{w}}_{i_{1}, j} (1 - π_{i}^{- 1}) (1 - π_{j}^{- 1}) cov (I (ε_{j} \leq t - m_{i} + {\tilde{d}}_{i, j}), I (ε_{j} \leq t - m_{j})), \end{array}$

et finalement

$E_{5} := \frac{1}{N^{2}} \sum_{i_{1} \in s} \sum_{i_{2} \in s} \sum_{j \in s, j \neq i_{2}} {\tilde{w}}_{i_{1}, j} (1 - π_{i_{1}}^{- 1}) (1 - π_{i_{2}}^{- 1}) \times cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) .$

Pour commencer, considérons $E_{1}$ et $E_{2} .$ Notons que, à part i) le fait que les indices de sommation $i_{1}$ et $i_{2}$ s’étendent sur $s$ au lieu du complément de $s$ dans $U,$ ii) la présence des facteurs $(1 - π_{i}^{- 1})$ et iii) le fait que les $w_{i, j}$ et les $d_{i, j}$ sont remplacés par leurs équivalents pondérés selon le plan de sondage ${\tilde{w}}_{i, j}$ et ${\tilde{d}}_{i, j},$ $E_{1}$ et $E_{2}$ sont semblables à $D_{1}$ et $D_{2}$ provenant de $var ({\hat{F}}^{*} (t) - F_{N} (t)),$ respectivement. L’adaptation des preuves qui mènent aux développements asymptotiques pour $D_{1}$ et $D_{2}$ montre donc que

$\begin{array}{l} E_{1} & = \frac{1}{n} {(\frac{N - n}{N})}^{2} \int_{a}^{b} [G (t - m (x) | x) - G^{2} (t - m (x) | x)] {[1 - π^{- 1} (x)]}^{2} h_{s} (x) d x + o (n^{- 1}) \end{array}$

et que

$E_{2} = o (λ^{5} + n^{- 1}) .$

Comme pour $E_{3},$ on constate immédiatement que

$E_{3} = E_{1} + o (n^{- 1}),$

tandis que, pour traiter $E_{4}$ et $E_{5},$ on a besoin des développements asymptotiques pour

$cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) (A .21)$

pour le cas où $j = i_{2}$ et celui où $j \neq i_{2} .$ Dans le premier cas, nous pouvons faire appel à des arguments similaires à ceux utilisés pour prouver (A.9) et (A.10), ce qui donne

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{j} \leq t - m_{j})) \\ = G (t - m_{i_{1}} \land t - m_{j} | x_{j}) - G (t - m_{i_{1}} | x_{j}) G (t - m_{j} | x_{j}) + O (λ^{2} + {(n λ)}^{- 1 / 2}) . \end{array}$

Par contre, quand $j \neq i_{2},$ la covariance dans (A.21) diffère de zéro uniquement si $| x_{j} - x_{i_{2}} | \leq λ$ ou $| x_{i_{1}} - x_{i_{2}} | \leq λ,$ et en adaptant (A.12), on peut montrer que

$\begin{array}{l} E (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}) I (ε_{i_{2}} \leq t - m_{i_{2}})) \\ = E (E (I (ε_{j} \leq {\tilde{a}}_{i_{1}, j, i_{2}} + {\tilde{b}}_{i_{1}, j, i_{2}} ε_{i_{2}}) I (ε_{i_{2}} \leq t - m_{i_{2}}) | ε_{k}, k \neq i, j)) \\ = E (\int_{- \infty}^{t - m_{i_{2}}} G ({\tilde{a}}_{i_{1}, j, i_{2}} + {\tilde{b}}_{i_{1}, j, i_{2}} ε | x_{j}) d G (ε | x_{i_{2}})) \\ = G (t - m_{i_{1}} | x_{j}) G (t - m_{i_{2}} | x_{i_{2}}) + G (t - m_{i_{2}} | x_{i_{2}}) G^{(1, 0)} (t - m_{i_{1}} | x_{j}) E (d_{i_{1}, j}) \\ + G^{(1, 0)} (t - m_{i_{1}} | x_{j}) {\tilde{b}}_{i_{1}, j, i_{2}} γ_{i_{2}, i_{2}} + \frac{1}{2} G (t - m_{i_{2}} | x_{i_{2}}) G^{(2, 0)} (t - m_{i_{1}} | x_{j}) E (d_{i_{1}, j}^{2}) \\ + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}), \end{array}$

où ${\tilde{a}}_{i, j, k}$ et ${\tilde{b}}_{i, j, k}$ sont les équivalents pondérés selon le plan de sondage de $a_{i, j, k}$ et $b_{i, j, k},$ respectivement. En adaptant également (A.4) pour tenir compte des poids de sondage, on constate que

$\begin{array}{l} cov (I (ε_{j} \leq t - m_{i_{1}} + {\tilde{d}}_{i_{1}, j}), I (ε_{i_{2}} \leq t - m_{i_{2}})) & = G^{(1, 0)} (t - m_{i_{1}} | x_{j}) {\tilde{b}}_{i_{1}, j, i_{2}} γ_{i_{2}, i_{2}} + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}) \\ = G^{(1, 0)} (t - m_{i} | x_{j}) ({\tilde{w}}_{j, i_{2}} - {\tilde{w}}_{i_{1}, i_{2}}) γ_{i_{2}, i_{2}} + o_{i_{1}, i_{2}, j} (λ^{4} + {(n λ)}^{- 1}) \end{array}$

de sorte que (voir les étapes qui mènent aux développements asymptotiques des termes $D_{1}$ et $D_{2}$ dans la variance de l’estimateur en deux étapes fondé sur le modèle)

$E_{4} = E_{1} + o (n^{- 1})$

$E_{5} = o (λ^{5} + n^{- 1}) .$

Cela achève la preuve de (A.20) et donc (A.19) s’ensuit.

Bibliographie

Breidt, F.J., et Opsomer, J.D. (2000). Local polynomial regression estimators in survey sampling. The Annals Statistics, 28(4), 1026-1053.

Chambers, R.L., et Clark, R. (2012). An Introduction to Model-Based Survey Sampling with Applications, Oxford Statistical Science Series 37.

Chambers, R.L., et Dunstan, R. (1986). Estimating distribution functions from survey data. Biometrika, 73(3), 597-604.

Chambers, R.L., Dorfman, A.H. et Wehrly, T.E. (1993). Bias robust estimation in finite populations using non-parametric calibration. Journal of the American Statistical Association, 88(421), 268-277.

Chen, J., et Wu, C. (2002). Estimation of distribution function and quantiles using the model-calibrated pseudo empirical likelihood method. Statistica Sinica, 12, 1223-1239.

Dorfman, A.H., et Hall, P. (1993). Estimators of the finite population distribution function using nonparametric regression. The Annals of Statistics, 21(3), 1452-1475.

Fan, J., et Gijbels, I. (1992). Variable bandwidth and local linear regression smoothers. The Annals of Statistics, 20(4), 2008-2036.

Hansen, B.E. (2008). Uniform convergence rates for kernel estimation with dependent data. Econometric Theory, 24, 726-748.

Johnson, A.A., Breidt, F.J. et Opsomer, J.D. (2008). Estimating distribution functions from survey data using nonparametric regression. Journal of Statistical Theory and Practice, 2(3), 419-431.

Kuo, L. (1988). Classical and prediction approaches to estimating distribution functions from survey data. Dans les Proceedings of the Survey Research Methods Section, American Statistical Association, Alexandria, VA, 280-285.

Montanari, G.E., et Ranalli, M.G. (2005). Nonparametric model calibration estimation in survey sampling. Journal of the American Statistical Association, 100(472), 1429-1442.

Rao, J.N.K., Kovar, J.G. et Mantel, H.J. (1990). On estimating distribution functions and quantiles from survey data using auxiliary information. Biometrika, 77(2), 365-375.

Rueda, M., Martínez, S., Martínez, H. et Arcos, A. (2007). Estimation of the distribution function with calibration methods. Journal of Statistical Planning and Inference, 137(2), 435-448.

Rueda, M., Sànchez-Borrego, I., Arcos, A. et Martínez, S. (2010). Model-calibration estimation of the distribution function using nonparametric regression. Metrika, 71(1), 33-44.

Särndal, C.-E., Swensson, B. et Wretman, J. (1992). Model Assisted Survey Sampling, New York : Springer.

Wang, J.C., et Opsomer, J.D. (2011). On asymptotic normality and variance estimation for nondifferentiable survey estimators. Biometrika, 98(1), 91-106.

Wu, C. (2003). Optimal calibration estimators in survey sampling. Biometrika, 90(4), 937-951.

Wu, C., et Sitter, R.R. (2001). A model-calibration approach to using complete auxiliary information from survey data. Journal of the American Statistical Association, 96(453), 185-193.

ISSN : 1712-5685

Politique de rédaction

Techniques d’enquête publie des articles sur les divers aspects des méthodes statistiques qui intéressent un organisme statistique comme, par exemple, les problèmes de conception découlant de contraintes d’ordre pratique, l’utilisation de différentes sources de données et de méthodes de collecte, les erreurs dans les enquêtes, l’évaluation des enquêtes, la recherche sur les méthodes d’enquête, l’analyse des séries chronologiques, la désaisonnalisation, les études démographiques, l’intégration de données statistiques, les méthodes d’estimation et d’analyse de données et le développement de systèmes généralisés. Une importance particulière est accordée à l’élaboration et à l’évaluation de méthodes qui ont été utilisées pour la collecte de données ou appliquées à des données réelles. Tous les articles seront soumis à une critique, mais les auteurs demeurent responsables du contenu de leur texte et les opinions émises dans la revue ne sont pas nécessairement celles du comité de rédaction ni de Statistique Canada.

Présentation de textes pour la revue

Techniques d’enquête est publiée en version électronique deux fois l’an. Les auteurs désirant faire paraître un article sont invités à le faire parvenir en français ou en anglais en format électronique et préférablement en Word au rédacteur en chef, (statcan.smj-rte.statcan@canada.ca, Statistique Canada, 150 Promenade du Pré Tunney, Ottawa, (Ontario), Canada, K1A 0T6). Pour les instructions sur le format, veuillez consulter les directives présentées dans la revue ou sur le site web (www.statcan.gc.ca/Techniquesdenquete).

Note de reconnaissance

Le succès du système statistique du Canada repose sur un partenariat bien établi entre Statistique Canada et la population, les entreprises, les administrations canadiennes et les autres organismes. Sans cette collaboration et cette bonne volonté, il serait impossible de produire des statistiques précises et actuelles.

Normes de service à la clientèle

Statistique Canada s'engage à fournir à ses clients des services rapides, fiables et courtois. À cet égard, notre organisme s'est doté de normes de service à la clientèle qui doivent être observées par les employés lorsqu'ils offrent des services à la clientèle.

Droit d'auteur

Publication autorisée par le ministre responsable de Statistique Canada.

L'utilisation de la présente publication est assujettie aux modalités de l'Entente de licence ouverte de Statistique Canada.

N° 12-001-X au catalogue

Périodicité : Semi-annuel

Ottawa

Date de modification :: 2016-06-22

Sélection de la langue

Recherche et menus

Recherche

Une comparaison d’estimateurs non paramétriques pour les fonctions de répartition de populations finies 5. Étude en simulationUne comparaison d’estimateurs non paramétriques pour les fonctions de répartition de populations finies 5. Étude en simulation

Remerciements

Annexe

Biais de l’estimateur fondé sur le modèle de Kuo

Biais de l’estimateur par la différence généralisée de Kuo

Variance de l’estimateur fondé sur le modèle de Kuo

Variance de l’estimateur par la différence généralisée de Kuo

Biais de l’estimateur fondé sur le modèle avec valeurs prédites modifiées

Biais de l’estimateur par la différence généralisée avec valeurs prédites modifiées

Variance de l’estimateur fondé sur le modèle avec valeurs prédites modifiées

Variance de l’estimateur par la différence généralisée avec valeurs prédites modifiées

Bibliographie