Privacy Preserving Technologies Part Two: Introduction to Homomorphic Encryption

By Zachary Zanussi, Statistics Canada

Have you ever wished that there was a way to access data to perform analytics while preserving the privacy of the data itself? Homomorphic encryption is an emerging privacy preserving technique with potential applications that will allow for greater access while keeping data encrypted and secure.

The first article in the series, Brief Survey of Privacy Preserving Technologies introduced privacy preserving techniques (PPTs) and how they are poised to enable analytics while protecting the privacy of the data. This article will build on that topic by taking a deeper look at one of these techniques, homomorphic encryption (HE), including what it is, how it works and what it can do for you.

This article begins with an overview of HE and introduces some common use cases. It gives an honest evaluation of HE's advantages and disadvantages. Then it will cover some of the more technical details to prepare you to dig into these techniques yourself! By the end of this article, hopefully you will be inspired to continue your learning by picking an HE library and making your own encrypted circuits.

Homomorphic encryption is currently being considered by international groups for standardization. The Government of Canada does not recommend that HE, or any cryptographic technique, be used in practice before standardization by experts. While HE is not yet ready for use on sensitive data, this is a great time to explore its functionality and potential use cases. Expect a future article on the standardization activities related to HE including expected timelines and schemes.

What is homomorphic encryption?

A traditional encryption scheme maps human-readable plaintexts into masked ciphertexts to protect data from prying eyes. Once masked, these ciphertexts are immutable; changing even a single bit in the ciphertext may return an unrecognizable plaintext message upon decryption. This makes traditional encryption quite static. By contrast, a homomorphic encryption scheme is dynamic; given two ciphertexts, you can perform operations on the underlying plaintexts. For example, a homomorphic 'add' operation will return a ciphertext that, upon decryption, returns the sum of the two original plaintext messages. This allows you to delegate computing to another party so that they can manipulate it without accessing the data.

A typical cloud computing protocol involves a client sending its data to the cloud. Since internet connections are inherently insecure, this transfer is facilitated by a form of transport security protocol that involves encryption, such as HTTPS. Upon receipt, the cloud decrypts and begins computation. However, what if you want to keep the data secret from the cloud? If you encrypted with a homomorphic scheme, not only would the data be protected during transport, but it would also be protected during the entire computation process. Upon completion, the cloud would forward the encrypted results back to the client, who could decrypt and view the results at their leisure.

The term "homomorphic" comes from Greek, roughly translating to "similar form." In mathematics, a homomorphism is a map from one mathematical structure to another that preserves the operations of the first structure. To construct a homomorphic encryption scheme, you need an encryption map that scrambles the data enough that no one can figure out what they are, while simultaneously preserving the structure of the data so that operations on ciphertexts result in predictable results in the plaintexts. These paradoxical goals underscore the difficulty in constructing such a scheme.

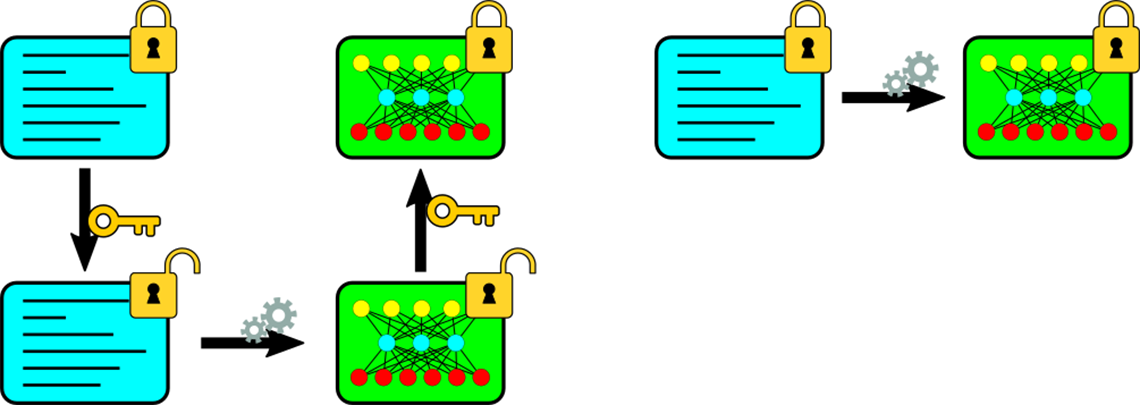
Figure 1: An illustration of the benefits of HE. On the left is ordinary encryption; to apply the desired analytics, the data need to first be decrypted using the private key. To make the results safe for transport, it must be re-encrypted. In addition, the data are vulnerable for the duration of the computation. On the right is HE; the computing party doesn't require any sensitive information to perform the calculation and the data and results are protected by encryption.

What can you do with homomorphic encryption?

There are a number of different computing paradigms that can be enhanced with HE, including delegated computing, data sharing and data release. These different paradigms all revolve around the fact that the data holder, analyst and computing platforms are often different parties entirely and the aim is to reduce or remove the privacy concerns that arise when one of these parties shouldn't have access to the data. It is important to note that HE uses a weaker security model than traditional cryptography and that care will need to be taken to ensure that it is used securely in practice.^{Footnote 1}

Possibly the simplest application involves a data holder delegating their computing to another party, such as the cloud. In this scenario, a client encrypts their data and sends them along with some instructions to the cloud. The cloud can carry out those instructions homomorphically and return the encrypted results, learning nothing about the input, output or intermediate values. These instructions are modeled as circuits, which are sequences of arithmetic operations applied to some input. It should be noted that creating correct and efficient circuits with HE is not always straightforward, but theoretically there is no limit to the computations that can be run. For example, Statistics Canada has completed proof-of-concepts^{Footnote 2} applying statistical analysis and neural network training on encrypted data.

As an extension of the delegated computing scenario, consider a case where there are multiple data holders. These data sources want to share their data, but are prevented due to privacy issues. The exact outline depends on the trust model; however, HE may allow these different parties to each encrypt their data and share them with a central authority who has the power to compute homomorphically. These data sharing applications can allow for better analytics in scenarios where data are limited and sheltered. An example is an oncologist who wants to test their hypotheses; patient data are typically restricted to the treating hospitals and combining these sets not only increases the strength of the model, but removes geographic data biases. Therefore, allowing multiple hospitals to share their encrypted data and allowing the oncologist to compute on this joint encrypted dataset allows for better healthcare research and outcomes.

Consider also scenarios with a central data holder and several parties who want to perform analysis on these data. An example of this is Statistics Canada's Research Data Centres, which are hosted across Canada in secure facilities managed by the organization. Accredited researchers can gain special approval to access microdata within these secure sites. While secure, the approval process takes time and the researchers must be able to physically access these sites. With HE, the data centres may be able to host the data encrypted and give access to any party who requests it. This would cut down the administrative costs of adding a new researcher and would broaden access to data in line with Canada's Open Data Initiative.

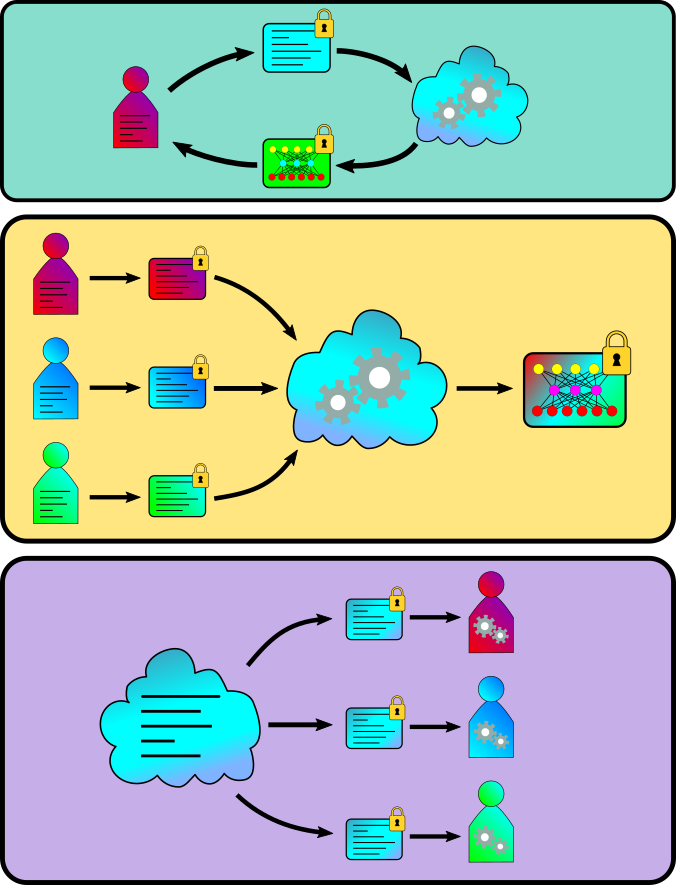
Figure 2: Illustrations of the three paradigms. First is delegated computing; the data holder encrypts and sends their data to the cloud, who returns the encrypted results after performing homomorphic calculations. Second, multiple parties encrypt and send their share of a distributed dataset which the cloud can use to perform analytics without compromising the privacy of each data holder. Third, a central data holder can give analysts access to an encrypted dataset. The analysts can be subjected to less scrutiny and restrictions because they never have direct access to the data.

HE can help with more than numerical calculations. For example, Private Set Intersection (PSI) allows a client in possession of a sensitive dataset to learn its intersection with a server's dataset without the server learning the client's dataset and without the client learning anything about the server's data beyond the intersection. Private String Matching is a similar protocol that allows the client to query a textual database for a matching substring. Using these and other cryptographic primitives, you can envision a broad privacy-preserving suite linking data dispersed across different government departments and public institutions. While such a system is ambitious and the exact implementations are not yet clear, it gives a taste of the types of systems that you can aspire to as more complicated tasks are completed using HE and other PPTs.

Downsides of homomorphic encryption

While there are many benefits to the use of HE, as with any technology, there are potential downsides. The price of cryptographic security is the computational cost; depending on the analysis, encrypted computation can be several orders of magnitude more expensive than unencrypted. There is also a data expansion cost that can be quite significant. This data expansion cost is exacerbated by the fact that most HE protocols involve transferring encrypted data; while cloud storage is relatively inexpensive, data transfer can be costly and complicated.

There are also a restricted set of computations allowed natively by HE. Only addition, subtraction and multiplication are native to most arithmetic schemes and all other computations (such as exponentials, activation functions, etc.) must be approximated by a polynomial. One should note that this is true in general with all computers, but while a modern computer hides this fact from the user, HE libraries currently require the user to specify how to compute these non-trivial functions.^{Footnote 3} In some schemes, one also has to be wary of the depth of computations attempted. Indeed, these schemes introduce noise into the encrypted data to protect it. This noise is compounded through successive computations and, unless reduced,^{Footnote 4} would eventually overtake the signal, at which point decryption will no longer return the expected output. One's choice of encryption parameters is important here. Given a circuit, there exists a parameter set large enough to accommodate it, but dealing with larger parameters increases the computational cost of the protocol.

Can the extra costs in terms of computation and circuit creation be justified? Well, HE allows for computations that might not be possible otherwise. This is true with particularly sensitive datasets, such as health data. There is a huge cost inherent in obtaining permissions for an analyst to work on such data, as well as additional complications such as controlled computing environments. And once the data are shared, how do you verify that the analysts are following the rules? Some data holders may be reluctant to allow anyone access to their data at all; without some additional measures such as HE, this analysis might be impossible. The choice between "expensive computation" and "no computation" is much easier to make.

Moreover, the various schemes and their implementations are an active area of research and the library implementations regularly release improvements to their data compression and homomorphic computation algorithms. There has also been a significant amount of investment in hardware acceleration for HE recently. This is similar to the hardware that is installed on most computers, which contains specific electronic circuits designed to perform encryption and decryption operations as fast as possible. This could allow HE-accelerated cloud computers to perform analysis on encrypted data at speeds closer to that of unencrypted data.

In spite of the downsides, there are reasons to believe that HE will become an important tool for preserving privacy. That makes the present a fantastic time to begin to examine what can be done with these techniques.

The mathematics of homomorphic encryption

Now this article will delve into the inner mathematical workings of HE, including cryptographic details; hopefully even non-mathematical readers will be able to grasp the basics of how these schemes work. It should be noted that the rest of this section provides details pertaining to the scheme of Cheon, Kim, Kim and Song, which they named Homomorphic Encryption for Arithmetic of Approximate Numbers but the cryptographic community usually refers to as CKKS. That said, most of what is mentioned here applies to the other schemes with only slight modifications.

At the heart of every public key cryptosystem is a mathematical problem that is believed to be hard to solve unless you have access to a special piece of information called a secret (or private) key. A related public key can be used to encrypt plaintext data producing a ciphertext, but only knowledge of the secret key enables one to recover the original plaintext from this ciphertext. Since the public key cannot be used to decrypt, the public key can be shared with anyone wishing to encrypt data with confidence that only the secret key holder can decrypt the ciphertext to access the plaintext.

Most HE schemes use some variant of the Learning With Errors hardness assumption. This describes the ring variant, called Ring-Learning With Errors (RLWE). Rather than integers, it deals with polynomials with integer coefficients. More precisely, you want the space of polynomials with integer coefficients modulo $q$ of degree less than $N$ ; this is denoted by $R_q=Z_q\left[X\right]/⟨X^N-1⟩$ . You can think of this space simply as lists of $N$ integers, each less than $q$ . Typically, you would take these values to be quite large; for example $N=2^{15}=16,384$ and $q ~ 2^{800}$. This makes $R_q$ large enough to hide secrets in! Figure 3 gives a toy example of the type of space we would work with.

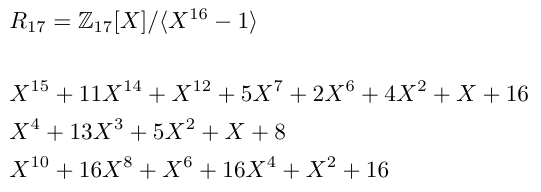
Figure 3: A toy example of a ring of the type that might be used for HE, as well as a few of its elements. Note that the sum or product of these elements is another element in the ring.

Given two polynomials, you can add them or multiply them. The result of these operations is always another polynomial.^{Footnote 5} This makes $R_q$ a kind of a sandbox that you can move around freely within. Mathematicians call a set with this property a ring and the way that these operations affect the elements of the ring is what is meant by structure. The special property of homomorphic encryption is that there exist operations in the ciphertext space that correspond homomorphically to the operations on the underlying plaintext space. The use of polynomial rings is preferred because the operations are efficient and the RLWE problem is believed to be difficult.

How does one hide a secret in a mathematical space? Suppose you have four random polynomials^{Footnote 6} in $R_q$ , called $a,s,e$ , and $b$. The RLWE hardness assumption states that it is very hard to distinguish a series of pairs that are either of the form $(a,a\cdot s+e)$ or of the form $(a,b).$Here, "very hard to distinguish" means "parameters can be set such that all the best computers in the world working together using the best known algorithms would still not be able to solve the problem. The polynomials $a$ and $b$ can be sampled uniformly at random from all of $R_q$, but the others have a special form. In CKKS, we take $s$ to have coefficients of $\pm 1$ or $0$, and sample the coefficients of $e$ from a discrete Gaussian distribution over $Z_q$ centred around $0$. For the rest of this post, we will just refer to these polynomials as "small", because in both cases their coefficients are close to $0$.

The hardness of the RLWE problem allows you to keep a secret in the following way: notice that the first pair is correlated; there is a factor of $a$ in both polynomials, while in the second there is no correlation between the randomly selected $a$ and $b$. Now imagine someone handed you many pairs that are either all of the form $(a,a\cdot s+e)$ for many different values of $e$ and $a$ constant $s$, or all just completely random pairs. According to the hardness of RLWE, not only could you not reliably find $s$ when given the $(a,a\cdot s+e)$ pairs, you couldn't even reliably determine which of type ofthe pairs you were given! Figure 4 gives a toy example of this problem for you to try at home.

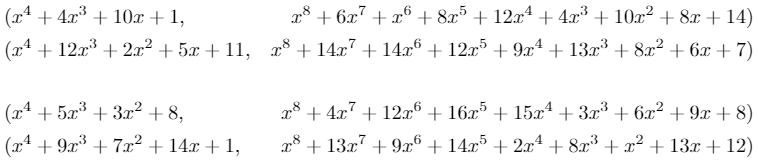
Figure 4: Four pairs of polynomials in$R_{17}=Z_{17}\left[X\right]/⟨X^{16}-1⟩$ broken into two groups. One group is distributed as form $(a,a\cdot s+e)$ for some fixed "small" $s$ and two different random "small" $e$ and the other two are of group is of the form $(a,b)$. Can you tell which is which? What if $17$ is changed to $2^{800}$ and $16$ to $16,384$? Now imagine trying to figure out what $s$ is. Note that in the RLWE assumption, you would be given just one of these groups, not both.

The security of schemes based on RLWE follows from the fact that given $a,s$ , and $e$ it is easy to compute $a\cdot s+e$, but it is practically impossible to find $s$ given $a$ and $a\cdot s+e$. You can construct a public key encryption system as follows:

• Fix your space $R_q$ by picking a coefficient modulus $q$ and a polynomial modulus degree $N$ .
• Pick a random "small" secret key $s$ , a uniformly random $a$, and a random "small" $e$ to construct your public key $(a,-a\cdot s+e,a)$. Note the negative in this pair; this makes the encryption process more straightforward but does not affect the security of RLWE.
• Share your public key with the world and no one will be able to find your secret key! Hence, anyone in possession of this public key can encrypt the data and send them to some party to perform computations on it, homomorphically. In the end, the results also can only be decrypted and viewed using the secret key.

To encrypt the data, the data must first be encoded as a vector $v$ of real numbers. This is straightforward when you are working with numerical data and is a standard practice when working with textual or other types of data. To encrypt, the data vector $v$ is first encoded as a polynomial^{Footnote 7} $m$ in $R_q$ combined with by the public key to get a ciphertext, which will be denoted by $\left[v\right]$ . Now, send this off to the computing party who will perform homomorphic additions and multiplications to implement the calculation that is of interest. Figure 5 outlines a simple circuit computing a polynomial function. Once the computations are completed and output ciphertexts are returned, you can use your secret key to decrypt and view the results.

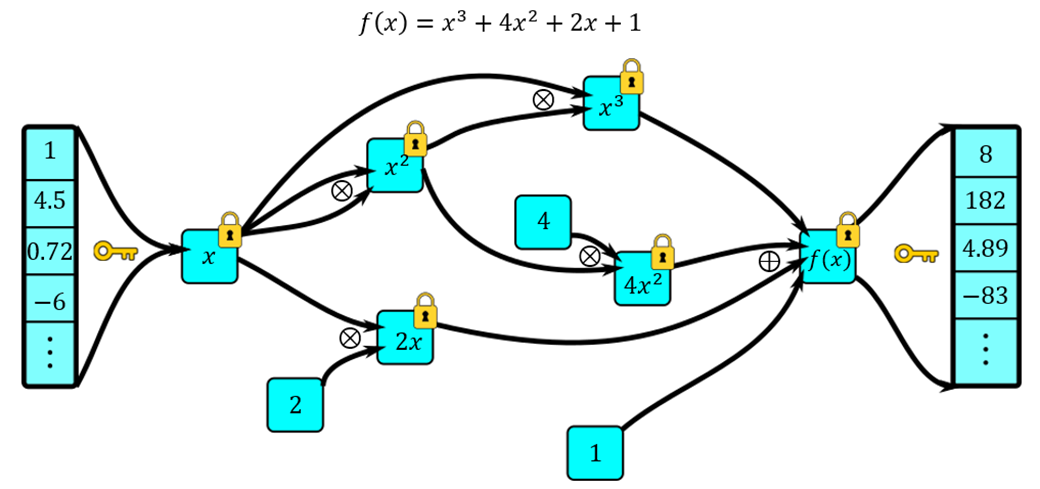
Figure 5: A visualization of a homomorphic circuit. A vector of values can be encrypted into a single ciphertext and computed on at once. Pictured is just one realization of a circuit to compute the polynomial $f\left(x\right)$. Values with padlocks are encrypted and are thus unreadable to the computing party.

While this article did not explore all of the details of how these operations are implemented mathematically, the description of HE given so far provides the background needed to further learn about HE.

How to get started with homomorphic encryption

To get started with HE, take a look at some of the available open-source HE libraries; you can try Microsoft SEAL, PALISADE Homomorphic Encryption Software Library, TFHE: Fast Fully Homomorphic Encryption over the Torus, or even Concrete: Open-source Homomorphic Encryption Library if you are a Rustacean also known as someone who uses Rust. These different libraries implement multiple HE schemes between them and you can pick the one that's best for your use case. We reiterate that, until the standardization process has finished, the Government of Canada does not recommend using HE with any sort of sensitive data.

While all of the different HE schemes will implement most use cases, some schemes will perform better on some problems. The CKKS scheme is designed to work on real numbers; if you are interested in statistics or machine learning, you should probably start here! Brakerski/Fan-Vercauteren and Brakerski-Gentry-Vaikuntanathan are great for integer arithmetic and implementing the computer science primitives such as private set intersection or string matching. TFHE implements logical gates natively and refreshes the ciphertext noise with every operation, allowing improved efficiency with longer circuit depths. Readers who are interested are encouraged to try some simple circuits using each scheme and compare the results and performance!

If you would like more information on the cyber security aspects of homomorphic encryption, including standardization activities, contact the Canadian Centre for Cyber Security at contact@cyber.gc.ca, (613) 949-7048 or 1-833-CYBER-88.

Conclusion

This article took an in-depth look at homomorphic encryption, from its applications to the RLWE problem. Next, this series on privacy preserving techniques will look at some proofs-of-concept that have been completed by applying HE at Statistics Canada! It will also cover some of the more advanced aspects of the CKKS interface, including rotations, choice of parameters, packing, bootstrapping, scale and levels.

Want to keep in the loop about these emerging technologies, or want to share your work in the field of privacy? Check out the Privacy Preserving Technologies Community of Practice page (Government of Canada employees only) to discuss this series of privacy articles, connect with peers interested in privacy and share resources and ideas with the community. You can also give feedback on this topic or leave suggestions for future articles in this series.

Note: We wish to acknowledge the input provided on this article by the Canadian Centre for Cyber Security and the Tutte Institute for Mathematics and Computing, both part of Communications Security Establishment.