4 Étude de la courbe de consommation moyenne d'électricité

Hervé Cardot, Alain Dessertaine, Camelia Goga, Étienne Josserand et Pauline Lardin

Précédent | Suivant

Nous disposons d'une population $U$ composée de $N=15069$ courbes de consommation électrique mesurées toutes les demi-heures pendant deux semaines consécutives. Nous avons $D=336$ points de mesure pour chaque semaine et nous souhaitons estimer la courbe moyenne de consommation de la deuxième semaine. On note $Y{\prime }_k=\left(Y_k\left(t_1\right)\mathrm{,}\dots \mathrm{,}{Y}_k\left(t_D\right)\right)\mathrm{,}$ la consommation d'électricité de l'individu $k\in U$ mesurée la deuxième semaine et $X{\prime }_k=\left(X_k\left(t_1\right)\mathrm{,}\dots \mathrm{,}{X}_k\left(t_D\right)\right)$ sa consommation au cours de la première semaine. La consommation moyenne de chaque individu $k$ durant la première semaine, $x_k={\displaystyle {\sum }_{d=1}^D{X}_k\left(t_d\right)/D}\mathrm{,}$ qui est une information simple et peu coûteuse à transmettre, sera utilisée comme information auxiliaire. 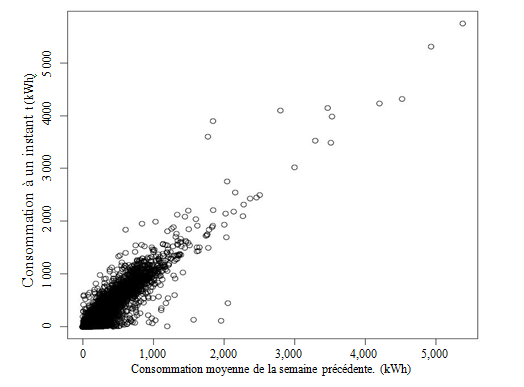Cette variable (réelle) qui est connue pour tous les éléments $k$ de la population est fortement liée à la courbe de consommation courante. On note sur la figure 4.1 que la consommation courante en chaque $t$ est quasiment proportionnelle à la consommation moyenne de la semaine précédente.

Description de la figure 4.1

Figure 4.1 : Représentation de la consommation à un instant $t$ en fonction de la consommation moyenne de la semaine précédente.

4.1  Description des stratégies utilisées

Nous considérons des échantillons de taille fixe $n=1500$ obtenus selon différents plans de sondage. Les stratégies présentées sont répétées $I$ fois afin d'évaluer et de comparer leurs performances.

1. ÉASSR et estimateur de Horvitz-Thompson.

La mise en œuvre de ce plan est simple, l'estimateur de Horvitz-Thompson de la courbe moyenne est donné par (2.6) et l'estimateur de sa covariance par (2.7).

2. Sondage stratifié STRAT et estimateur de Horvitz-Thompson.

Le plan stratifié est très efficace si les strates sont homogènes par rapport à la variable d'intérêt. Dans ce travail, nous avons utilisé l'algorithme des $k$ -means afin de constituer les strates et nous avons considéré $H=10$ strates. Une première stratification (STRAT 1) a été effectuée à partir de la classification des trajectoires discrétisées ${X^{\prime }}_k$ de la première semaine. Une seconde stratification, qui utilise uniquement l'information agrégée $x_k$ a également été considérée. Elle est notée STRAT 2.

Les tailles des strates $N_h$ obtenues en utilisant les deux stratifications ainsi que les tailles $n_h$ optimales, selon (2.5), des échantillons à sélectionner dans chaque strate sont données dans les tableaux 4.1 et 4.2. Dans les deux cas, les strates sont numérotées en ordre croissant par rapport à la consommation moyenne de chaque strate. Plus précisement, la strate 1 correspond aux faibles consommateurs et la strate 10 est composée des 10 plus gros consommateurs d'électricité. Notons que la première stratification, qui nécessite de connaître la consommation d'électricité à chaque instant de mesure $t,$ exige plus d'information que la deuxième stratification. La courbe moyenne est construite en utilisant (2.3) et sa covariance est estimée par (2.4).

Tableau 4.1
STRAT 1 : stratification à partir des courbes. Les strates sont construites à partir des courbes de la semaine 1. L'allocation $n_h$ optimale est calculée à partir des courbes de la semaine 1.
Sommaire du tableau
Le tableau montre la stratification à partir des courbes. Les données sont présentées selon h (titres de rangée) et 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 (figurant comme en-tête de colonne).

h	1	2	3	4	5	6	7	8	9	10
N h	3 866	4 769	623	2 690	664	1 251	806	328	62	10
n h	212	345	87	242	117	179	172	101	35	10

 

Tableau 4.2
STRAT 2 : stratification à partir de la consommation moyenne $x_k.$ L'allocation optimale $n_h$ est calculée à partir de la consommation moyenne de la semaine 1.
Sommaire du tableau
Le tableau montre la stratification à partir de la consommation moyenne $x_k.$. Les données sont présentées selon h (titres de rangée) et 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 (figurant comme en-tête de colonne).

h	1	2	3	4	5	6	7	8	9	10
N h	3 257	4 236	3 139	1 937	1 189	731	415	125	30	10
n h	260	293	248	204	159	133	111	56	26	10

3. Sondage $\pi ps$ et estimateur de Horvitz-Thompson.

Nous avons utilisé l'algorithme du cube proposé par Deville et Tillé (2004) et Chauvet et Tillé (2006) où les probabilités d'inclusion sont proportionnelles à $x_k\mathrm{,}k\in U$. Afin d'avoir un plan de sondage proche de l'entropie maximale, un tri aléatoire de la population est effectué avant le tirage de l'échantillon $s\mathrm{.}$ La covariance de l'estimateur de la moyenne est estimée à l'aide de la formule (2.9). L'algorithme du cube est disponible sous R dans le package sampling, fonction samplecube et une macro SAS est disponible sur le site web de l'INSEE (Institut National de Statistique et des Etudes Economiques).

4. ÉASSR et estimateur MA.

L'estimateur ${\widehat{\mu }}_{MA}$ assisté par le modèle $\xi$ est construit à l'aide de l'information auxiliaire donnée par $x{\prime }_k=\left(\mathrm{1,}{x}_k\right)$ où $x_k$ est la consommation moyenne de la semaine précédente. Dans ces conditions, ${\widehat{\mu }}_{MA}$ est la somme sur toute la population $U$ des valeurs estimées ${\widehat{Y}}_k$ par le modèle (voir formule (2.13)). La covariance de l'estimateur de la moyenne est estimée à l'aide de la formule (2.15).

4.2  Erreur d'estimation de la courbe moyenne

L'erreur d'estimation de la courbe moyenne $\mu$ aux instants $t_1\mathrm{,}\dots \mathrm{,}{t}_{336}\mathrm{,}$ est évaluée selon le critère

$$R_2\left(\widehat{\mu }\right)=\frac{1}{336}{\displaystyle \sum _{i=1}^{336}}{\left(\widehat{\mu }\left(t_i\right)-\mu \left(t_i\right)\right)}^2\approx \frac{1}{T}{\displaystyle {\int }_0^T}{\left(\widehat{\mu }\left(t\right)-\mu \left(t\right)\right)}^{2}dt\mathrm{.}$$

Les résultats sont présentés dans le tableau 4.3 pour $I=10000$ simulations (réplications). Ils montrent clairement que, pour cette étude, la prise en compte de la consommation totale de la semaine précédente permet d'améliorer de manière importante la précision de l'estimation de la moyenne par rapport à l'échantillonnage aléatoire simple sans remise en divisant l'erreur quadratique moyenne $R_2$ par 5. Parmi les différentes stratégies, les plus performantes semblent être celles qui prennent en compte l'information auxiliaire via les probabilités d'inclusion (STRAT, $\pi ps$ et systématique proportionnel à la taille).

Tableau 4.3
Erreur quadratique $R_2$ d'estimation de la moyenne $\mu ,$ avec $I=10000$ réplications.
Sommaire du tableau
Le tableau montre l'erreur quadratique $R_2$ d'estimation de la moyenne $\mu ,$ avec $I=10000$ réplications.. Les données sont présentées selon stratégie (titres de rangée) et moyenne, 1^erquartile, médiane, 3^eme (figurant comme en-tête de colonne).

Stratégie	moyenne	1 er quartile	médiane	3 emequartile
ÉASSR	40,53	10,82	22,16	51,09
STRAT (1)	5,78	3,68	5,08	7,07
STRAT (2)	6,49	4,03	5,48	7,88
$\pi ps$	7,06	3,99	5,52	8,16
$\pi -ps$ systématique	6,73	3,85	5,20	8,07
MA	8,29	5,24	7,14	10,06

4.3  Taux de couverture et largeur des bandes de confiance

La construction des bandes de confiance de niveau $1-\alpha$ nécessite le calcul des quantiles d'ordre $1-\alpha$ du supremum de processus gaussiens.

Pour ne pas privilégier une méthode de construction de bande de confiance par rapport à l'autre, nous avons appliqué les deux algorithmes sur un même échantillon et nous avons considéré le même nombre $M$ de processus. Ce nombre $M$ varie d'un estimateur à l'autre en raison des temps de calculs nécessaires pour les approches de type bootstrap (voir Section 4.4).

Description de la figure 4.2

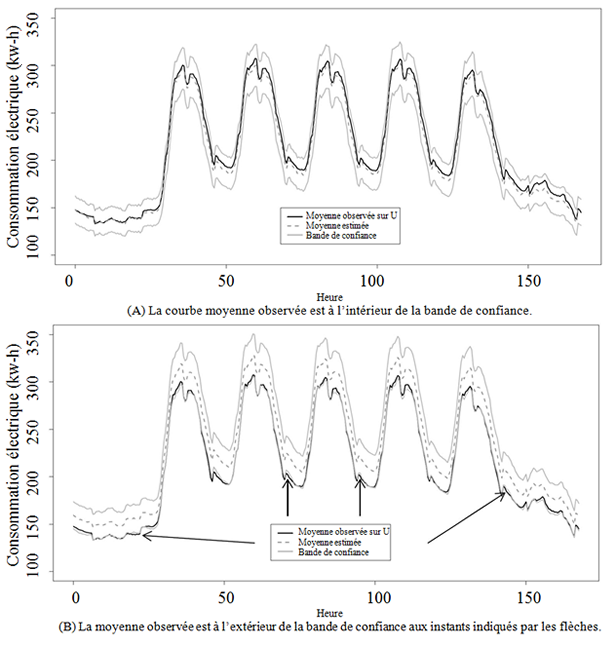
Figure 4.2 : Exemples de bande de confiance.

Le taux de couverture empirique est la proportion de fois, parmi les $I=2000$ réplications, où la vraie courbe moyenne $\mu$ se trouve, pour tous les instants $t\mathrm{,}$ à l'intérieur de la bande de confiance construite à partir d'une estimation $\widehat{\mu }$. Nous avons représenté sur la figure 4.2 deux exemples de bandes de confiance (courbes grises continues) construites à partir des courbes estimées (courbes grises pointillées). Sur la figure 4.2(A), nous constatons que la vraie courbe moyenne sur la population (courbe noir continue) est à l'intérieur de la bande de confiance à chaque instant. À l'opposé, sur la figure 4.2(B), nous constatons que la courbe moyenne de la population est en général surestimée et qu'il existe quelques instants (indiqués par les flèches) où la courbe observée sort de la bande de confiance. Les taux de couverture empiriques sont présentés dans le tableau 4.4.

Les deux méthodes de construction des bandes de confiance donnent des taux de couverture similaires et assez proches des taux nominaux souhaités (95 % et 99 %). Les résultats semblent cependant légèrement moins satisfaisants pour les plans $\pi ps$ et pour l'approche MA pour lesquels la variance de l'estimateur est complexe et plus difficile à estimer précisément.

Tableau 4.4
Taux de couverture empirique (en %), pour $I=2000$ réplications.
Sommaire du tableau
Le tableau montre le taux de couverture empirique (en %), pour $I=2000$ réplications. Les données sont présentées selon méthodes (titres de rangée) et nombre M de processus, bootstrap, processus Gaussien (figurant comme en-tête de colonne).

Méthodes	Nombre M de processus	Bootstrap		Processus Gaussien
		$\alpha =0.05$	$\alpha =0.01$	$\alpha =0.05$	$\alpha =0.01$
ÉASSR	5 000	94,95	98,85	94,80	98,70
STRAT (1)	5 000	93,92	98,34	94,09	98,43
STRAT (2)	5 000	94,3	98,45	94	98,55
$\pi ps$	1 000	94,73	98,77	93,87	98,61
MA	5 000	94,3	98,5	92,85	98,15

Un autre indicateur intéressant est la largeur moyenne de la bande de confiance,

$$\frac{1}{336}{\displaystyle \sum _{i=1}^{336}2c_{\alpha }\widehat{\sigma }\left(t_i\right)}\approx \frac{1}{T}{\displaystyle {\int }_0^T}2c_{\alpha }\widehat{\sigma }\left(t\right)dt$$

dont les valeurs sont présentées dans le tableau 4.5. Les deux méthodes fournissent des bandes de confiance dont les largeurs sont similaires. On note également que l'utilisation de la variable auxiliaire permet de diminuer sensiblement la largeur moyenne des bandes, celle-ci étant divisée par deux si on considère un des plans stratifiés plutôt qu'un plan d'ÉASSR.

Description de la figure 4.3

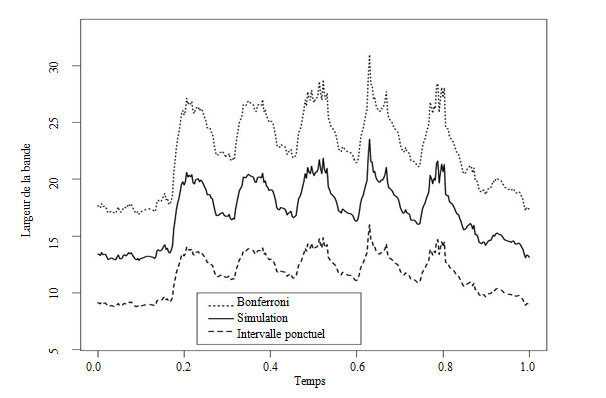
Figure 4.3 : Échantillonnage aléatoire simple sans remise. Largeur des bandes de confiance ponctuelles, globales par simulations de processus et avec Bonferroni ($\alpha =0,05$).

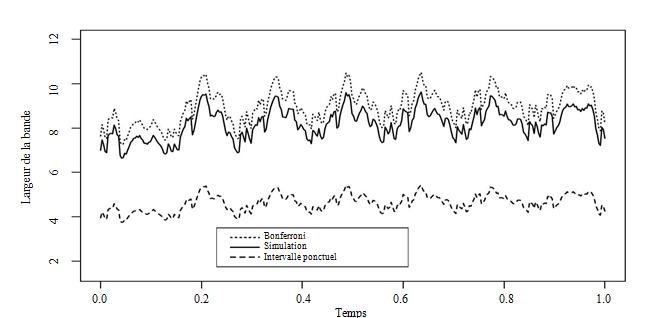
Description de la figure 4.4

Figure 4.4 : Sondage stratifié (STRAT 1). Largeur des bandes de confiance ponctuelles, globales par simulations de processus et avec Bonferroni (avec $\alpha =0,05$).

Les figures 4.3 et 4.4 présentent les largeurs des bandes de confiance pour un niveau $\alpha =0,05$, pour chaque instant, selon qu'elles soient ponctuelles ( $c_{\alpha }=1,96$ ), estimées par simulations de processus gaussiens ou bien obtenues en considérant l'approche basée sur l'inégalité de Bonferroni appliquée en chaque point de mesure. On a alors, dans ce dernier cas, $c_{\alpha }=3,793048$, le quantile d'ordre $1-0,05/\left(336\times 2\right)$ d'une loi $N\left(\mathrm{0,1}\right)$. Les bandes obtenues par Bonferroni sont conservatives et considèrent en quelque sorte le pire des cas en termes d'information, celui de l'indépendance des intervalles ponctuels. On peut remarquer que l'approche par simulation permet de réduire sensiblement la largeur moyenne des bandes en comparaison avec Bonferroni lorsque le plan ne permet pas de prendre en compte toute l'information temporelle des données (figure 4.3). À l'opposé, pour le plan stratifié (figure 4.4) qui permet une estimation précise de la courbe moyenne, la bande de confiance construite par simulation est proche de celle de Bonferroni, ce qui s'interprète intuitivement comme le fait que quasiment toute l'information a été capturée par le plan de sondage.

Tableau 4.5
Largeur moyenne des bandes de confiance, pour $I=2000$ réplications.
Sommaire du tableau
Le tableau montre la largeur moyenne des bandes de confiance, pour $I=2000$ réplications.. Les données sont présentées selon méthodes (titres de rangée) et nombre M de processus, bootstrap, processus Gaussien (figurant comme en-tête de colonne).

Méthodes	Nombre M de processus	Bootstrap		Processus Gaussien
		$\alpha =0.05$	$\alpha =0.01$	$\alpha =0.05$	$\alpha =0.01$
ÉASSR	5 000	35,98	43,35	35,99	43,19
STRAT (1)	5 000	16,64	18,92	16,62	18,88
STRAT (2)	5 000	17,58	19,99	17,55	19,94
$\pi ps$	1 000	17,85	20,31	17,62	19,93
MA	5 000	19,88	22,65	19,75	22,44

4.4 Temps de calcul

Les temps de calcul avec la méthode par bootstrap sont largement supérieurs, de l'ordre d'un facteur de 1 à 1000, à ceux de la méthode par simulations de processus gaussiens (voir tableau 4.6). Cette différence importante provient du fait que les méthodes de bootstrap nécessitent de répéter tout le processus d'estimation pour chaque échantillon bootstrapé : construction de la population fictive, tirage d'un nouvel échantillon, calcul de l'estimateur. On remarque également que les plans qui font intervenir de l'information auxiliaire sont moins rapides que le plan d'ÉASSR même si utilisés individuellement leur temps de calcul reste tout à fait raisonnable.

Tableau 4.6
Temps d'exécution d'une simulation en secondes pour $M=5000$ réplications. Les stratégies ÉASSR, MA et STRAT ont été programmés avec R et $\pi ps$ avec SAS.
Sommaire du tableau
Le tableau montre Temps d'exécution d'une simulation en secondes pour $M=5000$ réplications. Les stratégies ÉASSR, MA et STRAT ont été programmés avec R et $\pi ps$ avec SAS. Les données sont présentées selon stratégie (titres de rangée) et bootstrap, processus gaussiens (figurant comme en-tête de colonne).

Stratégie	Bootstrap	Processus gaussiens
ÉASSR	1 170,6	1,0
STRAT	1 839,5	1,4
$\pi ps$	5 020,0	7,3
MA	3 156	1,4

Précédent | Suivant