Microsimulation approaches
- Introduction
- Purposes of microsimulation: explanation versus prediction
- General versus specialized models
- Cohort versus population models
- Open versus closed population models
- Cross-sectional versus synthetic starting populations
- Continuous versus discrete time
- Case-based versus time-based models
Introduction
This document provides a breakdown of contrasting microsimulation approaches that come into play when we simulate societies with a computer. These approaches can in turn be broken down into approaches of purpose, scope, and methods on how populations are simulated.
With respect to purpose, we mainly distinguish between prediction and explanation, which turns out to also be the distinction in purpose between data-driven empirical microsimulation on one hand and agent based simulation on the other. The prediction approach is further subdivided into a discussion of projections versus forecasts.
There are two aspects covered on the scope of a simulation – we first distinguish general models from specialized ones, then population models from cohort models.
Finally, looking at the methods on how we simulate populations, we focus our discussion in three ways. The first is the population type we simulate, thereby enabling us to distinguish both open versus closed population models, as well as cross-sectional versus synthetic starting populations. The second is the time framework used, either discrete or continuous. The third is the order in which lives are simulated, leading to either a case-based or time-based model.
Purposes of microsimulation: explanation versus prediction
Modeling is abstraction, a reduction of complexity by isolating the driving forces of studied phenomena. The quest to find a formula for human behaviour, especially in economics, is so strong that over-simplified assumptions are an often accepted price for the beauty or elegance of models. The notion that beauty lies in simplicity is even found in some agent based models. Epstein draws an especially appealing analogy between agent based simulation and the paintings of French impressionists, one of these paintings (a street scene) being displayed on the cover of 'Generative Social Sciences' (Epstein 2006). Individuals in all their diversity are only sketched by some dots, but looking from some distance, we are able to clearly recognize the scene.
Can statistical and accounting models compete in beauty with the emergence of social phenomena from a set of simple rules? Hardly--they are complex in nature and require multitudes of parameters. While statisticians might still find elegance in regression functions, beauty is hard to maintain when it comes to filing tax returns or claiming pension benefits. Accounting is boring for most of us, and models based on a multitude of statistical equations and accounting rules can quickly become difficult to understand. So how can microsimulation models compensate for their lack in beauty? The answer is simple: usefulness. In essence, a microsimulation model is useful if it has predictive or explanatory power.
In agent based simulation, explanation means generating social phenomena from the bottom up, the generative standard of explanation being epitomized in the slogan: If you didn't grow it, you didn't explain it (which is regarded as a necessary but not sufficient condition for explanation). This slogan expresses the critique of the agent based community on the mainstream economics community, with the latter's focus on equilibriums without paying too much attention to how or if those equilibriums can ever be reached in reality. Again, agent based models follow a bottom-up approach of generating a virtual society. Their starting points are theories of individual behaviour expressed in computer code. The spectrum of how behaviour is modeled thereby ranges from simple rules to a distributed artificial intelligence approach. In the latter case, the simulated actors are 'intelligent' agents. As such, they have receptors; they get input from the environment. They have cognitive abilities, beliefs and intentions. They have goals, develop strategies, and learn from both their own experiences and those of other agents. This type of simulation is currently almost exclusively done for explanatory purposes. The hope is that the phenomena emerging from the actions and interactions of the agents in the simulation have parallels in real societies. In this way, simulation supports the development of theory.
The contrast to explanation lies in detailed prediction, which constitutes the main purpose of data-driven microsimulation. If microsimulation is designed and used operatively for forecasting and policy recommendations, such models "need to be firmly based in an empirical reality and its relations should have been estimated from real data and carefully tested using well-established statistical and econometric methods. In this case the feasibility of an inference to a real world population or economic process is of great importance" (Klevmarken, 1997).
To predict the future state of a system, there is also a distinction to make between projections and forecasts. Projections are 'what if' predictions. Projections are always 'correct', based on the assumptions that are provided (as long as there are no programming errors). Forecasts are attempts to predict the most likely future, and since there can only be one actual future outcome, most forecasts therefore turn out to be false. With forecasts, we are not just simply trying to find out 'what happens if' (as is the case with projections); instead, we aim to determine the most plausible assumptions and scenarios, thus yielding the most plausible resulting forecast. (It should be noted, however, that implausible assumptions are not necessarily without value. Steady-state assumptions are examples of assumptions that are conceptually appealing and therefore very common but usually implausible. Under such assumptions, individuals are aged in an unchanging world with respect to the socioeconomic context such as economic growth and policies, and the individual behaviour is 'frozen' not allowing for cohort or period effects. Since a cross-section of today's population does not result from a steady-state world, the 'freezing' of individual behaviour and the socioeconomic context can help to isolate and study future dynamics and phenomena resulting from past changes, such as population momentum.)
How different is explanation from prediction? Why can't we rephrase the previous slogan to: If you didn't predict it, you didn't explain it ? First, being able to produce good predictions does not necessarily imply a full understanding of the operations underlying the studied processes. We don't need a full theoretical understanding to predict that lightning is followed by thunder or that fertility is higher in certain life course situations than in others. Predictions can be fully based on observed regularities and trends. In fact, theory is often sacrificed in favour of a highly detailed model that offers a good fit to the data. This, of course, is not without danger. If behaviours are not modeled explicitly, then neither are the corresponding assumptions, which can make the models difficult to understand. We can end up with black-box models. On the other hand, agent based models, while capable of 'growing' some social phenomena, do so in a very stylized way. So far, these models have not reached any sufficient predictive power. In the data-driven microsimulation community, agent based models are thus often regarded as toy models.
Whatever the reason for developing a microsimulation model, however, modellers will typically experience one positive side effect from the exercise: the clarification of concepts. By modeling behaviour, a level of precision (eventually transferred into computer code) is required that is not always found in social science which has an abundance of pure descriptive theory. It is safe to say that the process of modeling itself generates new insights into the processes being modeled (e.g. Burch 1999). While some of these benefits can be experienced in all statistical modeling, simulation adds to the potential. By running a simulation model, we always gain insights into both the reality we are trying to simulate plus the operation of our models and the consequences of our modeling assumptions. In this sense, microsimulation models are always explorative tools, whether their main purpose is explanation or prediction. Or to put it differently, microsimulation models provide experimental platforms for societies where the possibility of genuine natural experiments is limited by nature.
General versus specialized models
The development of larger-scale microsimulation models typically requires a considerable initial investment. This is especially true for policy simulations. Even if only interested in the simulation of one specific policy, we have to create a population and model the demographic changes before we can add the economic behaviour and accounting routines necessary for our study. This can create a situation where it becomes more logical to design microsimulation models as 'general purpose' models, thereby attracting potential investors from various fields. A model capable of detailed pension projections might easily be extended to other tax benefit fields. A model including family structures might be extended to simulate informal care. A struggle for survival can even lead to rather exotic applications–for example, one of the largest models, the US CORSIM model, survived difficult financial times by receiving a grant from a dentist's association interested in a projection of future demands for teeth prosthesis!
It is not surprising, therefore, that there is a general tendency to plan and develop microsimulation applications as general, multi-purpose models right from the beginning. In fact, large general models currently exist for many countries, as shown in the following table.
| Country | Models |
|---|---|
| Australia: | APPSIM, DYNAMOD |
| Canada: | DYNACAN, LifePaths |
| France: | DESTINIE |
| Norway: | MOSART |
| Sweden: | SESIM, SVERIGE |
| UK: | SAGEMOD |
| USA: | CORSIM |
In creating general models, both the control of ambitions and modularity in the design are crucial for success. Only a few of today's large models have actually reached and stayed at their initially planned sizes. Overambitious approaches have had to be corrected by considerable simplifications, as was the case with DYNAMOD which was initially planned as an integrated micro – macro model.
Specialized microsimulation models concentrate on a few specific behaviours and/or population segments. An example is the NCCSU Long-term Care Model (Hancock et al., 2006). This model simulates the incomes and assets of future cohorts of older people and their ability to contribute towards home care fees. It thereby concentrates on the simulation of the means test of long-term care policies, with the results fed into a macro model of future demands and costs.
Historically, it has also been the case that some models which started off as rather specialized models ended up growing to more general ones. This happened with SESIM and LifePaths, both initially developed for the study of student loans. LifePaths is a particularly interesting example as it not only grew to a large general model but also constituted the base, in a stripped-off version, of a separate family of specialized health models (Statistics Canada's Pohem models).
Cohort versus population models
Cohort models are specialized models, as opposed to general ones, since they only simulate one population segment, namely one birth cohort. This is a useful simplification if we are only interested in studying one cohort or comparing two distinct cohorts.
Economic single cohort studies typically investigate lifetime income and the redistributive effects of tax benefit systems over the life course. Examples of this kind of model include the HARDING and LIFEMOD models developed in parallel, the former for Australia, and the latter for Great Britain (Falkingham and Harding 1996). This kind of model typically assumes a steady-state world, i.e., the HARDING cohort is born in 1960 and lives in a world that looks like Australia in 1986.
Population models deal with the entire population and not just specific cohorts. Not surprisingly, several limitations of cohort models are removed when simulating the whole population, including demographic change issues and distributional issues between cohorts (like intergenerational fairness).
Open versus closed population models
On a global scale, the human population is a closed one. Everybody has been born and will eventually die on this planet, has biological parents born on this planet, and interacts with other humans all sharing these same traits. But, when focusing on the population of a specific region or country, this no longer holds true. People migrate between regions, form partnerships with persons originating in other regions, etc. In such cases, we are dealing with open populations. Therefore, in a simulation model in which we are almost never interested in modeling the whole world population, how can we deal with this problem?
The solution usually requires a degree of creativity. For example, when allowing immigration, we will always have the problem to find ways to model a specific country without modeling the rest of the world. With respect to immigration, many approaches have been adopted, ranging from the cloning of existing 'recent immigrants' to sampling from a host population or even from different 'pools' of host populations representing different regions.
Conceptually more demanding is the simulation of partner matching. In microsimulation, the terms closed and open population usually correspond to whether the matching of spouses is restricted to persons within the population (closed) or whether spouses are 'created on demand' (open). When modeling a closed population, we have the problem that we usually simulate only a sample of a population and not the whole population of a country. If our sample is too small, it becomes unlikely that reasonable matches can be found within the simulated sample. This holds especially true if geography is also an important factor in our model. For example, if there are not many individuals representing the population of a small town, then very few of them will find a partner match within a realistic distance.
The main advantages of closed models are that they allow kinship networks to be tracked and that they enforce more consistency (assuming that they have a large enough population to find appropriate matches). Major drawbacks of closed models, however, are the sampling problems and computational demands associated with partner matching. In a starting population derived from a sample, the model may not be balanced with respect to kinship linkages other than spouses, since a person's parents and siblings are not included in the base population if they do not live in the same household (Toder et al. 2000).
The modeling of open populations requires some abstraction. Here, partners are created on demand - with characteristics synthetically generated or sampled from a host population – and are treated more as attributes of a 'dominant' individual than as 'full' individuals. While their life courses (or some aspects of interest for the simulation of the dominant individual) are simulated, they themselves are not accounted for as individuals in aggregated output.
Cross-sectional versus synthetic starting populations
Every microsimulation model has to start somewhere in time, thus creating the need for a starting population. In population models, we can distinguish two main starting population types: cross-sectional and synthetic. In the first case, we read in a starting population from a cross-sectional dataset and then age all individuals from this moment until death (while of course also adding new individuals at birth events). In the second case we follow an approach typically also found in cohort models–all individuals are modeled from their moment of birth onwards.
If we are only interested in the future, why would we want to start with a synthetic population that would also force us to simulate the past? Certainly, starting from a cross-sectional dataset can be simpler. When we start from representative 'real data', we therefore do not have to retrospectively generate a population, implying that we do not need historical data to model past behaviour. Nor do we have to concern ourselves with consistency problems, since simulations starting with synthetic populations typically lack full cross-sectional consistency.
Unfortunately, many microsimulation applications do need at least some biographical information not available in cross-sectional datasets. For example, past employment and contribution histories determine future pensions. As a consequence, some retrospective or historical modeling will typically be required in most microsimulation applications.
One idea to avoid a synthetic starting population when historical simulation is in fact needed could be to start from an old survey. This idea was followed in the CORSIM model which used a starting population from a 1960 survey (which also makes this model an interesting subject of study itself). While the ensuing possibility to create retrospective forecasts can help assess the model's quality against reality, such an approach nevertheless has its own problems. CORSIM makes heavy use of alignment techniques to recalibrate its retrospective forecasts to published data. Even if many group and aggregate outcomes can be exactly aligned to recent data, there is no way of assuring that the joint distributions based on the 1960 data remain accurate after several decades.
When creating a synthetic starting population, everything is imputed. We thus need models of individual behaviour going back a full century. While such an approach is demanding, it has its advantages. First, the population size is not limited by a survey; we are able to create larger populations, thus diminishing Monte Carlo variability. Second, being created synthetically, we omit confidentiality conflicts. (Statistics Canada follows this approach in its LifePaths model.) Overall, the more that past information has to be imputed, or the more crucial that past information is for what the application is attempting to predict or explain, then the more the approach of a synthetic starting population becomes attractive. For example, Wachter (Wachter 1995) simulated the kinship patterns of the US population following a synthetic starting population approach that went back to the early 19th century. Such detailed kinship information is not found in any survey and thus can be constructed only by means of microsimulation.
Continuous versus discrete time
Models can be distinguished by their time framework which can be either continuous or discrete. Continuous time is usually associated with statistical models of durations to an event, following a competing risk approach. Beginning at a fixed starting point, a random process generates the durations to all considered events, with the event occurring closest to the starting point being the one that is executed while all others are censored. The whole procedure is then repeated at this new starting point in time, and this cycle keep on occurring until the 'death' event of the simulated individual takes place.
Figure 1 illustrates the evolution of a simulated life course in a continuous time model. At the beginning, there are three events (E1, E2, E3), each of which has a randomly generated duration. In the example, E1 occurs first so it becomes the event that is executed; after that, durations for the three events are 're-determined'. However, because E3 is not defined to be contingent on E1 in the example, its duration remains unchanged, whereas new durations are re-generated for E1 and E2. E3 ends up having the next smallest duration so it is executed next. The cycle then continues as durations are again re-generated for all three events.
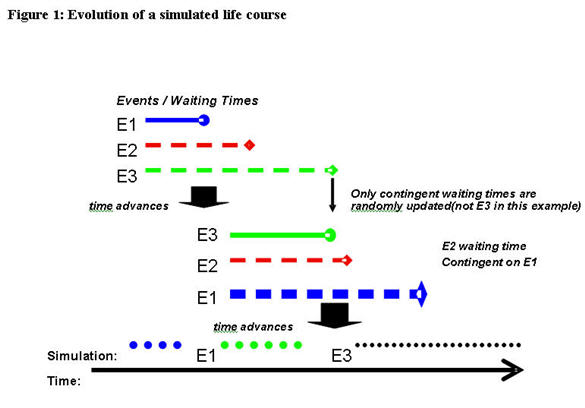
Continuous time models are technically very convenient, as they allow new processes to be added without changing the models of the existing processes as long as the statistical requirements for competing risk models are met (See Galler 1997 for a description of associated problems).
Modeling in continuous time, however, does not automatically imply that there are no discrete time (clock) events. Discrete time events can occur when time-dependent covariates are introduced, such as periodically updated economic indices (e.g. unemployment) or flow variables (e.g. personal income). The periodic update of indices then censors all other processes at every periodic time step. If the interruption periods are so short (e.g. one day) that the maximum number of other events within a period virtually becomes one, such a model has converged towards a discrete time model.
Discrete time models determine the states and transitions for every time period while disregarding the exact points of time within the interval. Events are assumed to happen just once in a time period. As several events can take place within one discrete time period, either short periods have to be used to avoid the occurrence of multiple events or else all possible combinations of single events have to be modeled as events themselves. Discrete time frameworks are used in most dynamic tax benefit models, with the older models usually using a yearly time framework mainly due to computational restrictions. With computer power becoming stronger and cheaper over time, however, shorter time steps can be expected to become predominant in future models. When time steps become so short that we can virtually exclude the possibility of multiple events, we have reached 'pseudo-continuity'. In this case we can even use statistical duration models. An example of the combination of both approaches is the Australian DYNAMOD model.
Case-based versus time-based models
The distinction between case-based and time-based models lies in the order in which individual lives are simulated. In case-based models one case is simulated from birth to death before the simulation of the next case begins. Cases can be individual persons or a person plus all 'non-dominant' persons that have been created on demand for this person. In the latter situation, all lives pertaining to a given case are simulated simultaneously over time.
Case-based modeling is only possible if there is no interaction between cases. Interactions are limited to the persons belonging to a case, thereby imposing significant restrictions on what can be modeled. The advantage of such models is of a technical nature--because each case is simulated independently of the others, it is easier to distribute the overall simulation job to several computers. Furthermore, memory can be freed after each case has been simulated, since the underlying information does not have to be stored for future use. (Case-based models can also only be used with open population models, not closed ones).
In time-base models, all individuals are simulated simultaneously over a pre-defined time period. Because all individuals are aging simultaneously (as opposed to just the individuals in one case), the computational demands definitely increase. In a continuous time framework, the next event that happens is the first event scheduled within the entire population. Thus, computer power can still be a bottleneck for this kind of simulation – current models in use typically have population sizes of less than one million.
- Date modified:
