par Stany Nzobonimpa, Mohamed Abou Hamed, Ilia Korotkine, Tiffany Gao, Logement, Infrastructures et Collectivités Canada
Remerciements
Les auteurs souhaitent remercier les personnes suivantes pour leur contribution et leur soutien au projet : Kate Burnett-Isaacs, directrice, Science des données et Matt Steeves, directeur principal de l’Ingénierie, des Opérations techniques et des Projets – Grands ponts et Projets.
Introduction
Dans le domaine de la science des données, le recensement et le signalement d’événements, tels que des points de données qui s’écartent de manière considérable du comportement normal ou attendu, sont connus sous le nom de détection d’anomalie. Les anomalies présentent un intérêt particulier pour les scientifiques de données, car elles signalent des problèmes sous-jacents qui éveillent des soupçons et justifient généralement de procéder à une enquête. Diverses techniques statistiques ont de tout temps été appliquées pour répondre aux questions relatives aux anomalies, et les progrès en matière d’intelligence artificielle (IA) ont fait de cet exercice l’une des applications les plus connues des approches et des cadres relatifs à l’apprentissage automatique.
Dans cet article, nous présentons et examinons les principales constatations d’un projet appliquant la détection d’anomalies aux données de capteurs. Le projet a été réalisé au sein de LICC par une équipe pluridisciplinaire de scientifiques de données et d’ingénieurs. Bien que le projet se déroule en plusieurs étapes, l’article présente les méthodes et les résultats de la première phase, au cours de laquelle les données de capteurs d’un pont fédéral ont été utilisées pour la détection précoce des relevés anormaux.
L’article est structuré comme suit : nous commençons par une brève revue de la littérature pertinente et récente sur la détection des anomalies et ses applications, où nous montrons que les méthodes de détection des anomalies dans les données ont évolué et continuent d’évoluer. Nous présentons par la suite la problématique, les méthodes et les résultats de cette première étape du projet. Plus particulièrement, nous montrons que l’approche nous a permis de signaler de manière proactive, plus rapidement et de manière moins laborieuse, des anomalies dans les données de capteurs générées qui auraient pu ne pas être détectées autrement. En effet, nos résultats montrent que pour la période d’avril 2020 à septembre 2024, un certain nombre de relevés de capteurs ont été correctement signalés comme des anomalies en utilisant les méthodes que nous présentons dans cet article. La conclusion précise les prochaines étapes du projet.
Revue de la littérature
L’application de l’apprentissage automatique pour la détection des anomalies
La détection d’anomalies est depuis longtemps un sujet d’intérêt dans le domaine de l’exploration de données, qui a jeté les bases de nombreuses approches modernes d’apprentissage automatique. Les travaux fondamentaux dans le domaine de l’exploration de données ont largement étudié les techniques de détection des anomalies, notamment les méthodes fondées sur le regroupement, la distance et la densité. Ainsi, la détection des anomalies est l’une des principales applications de la technologie d’apprentissage automatique qui est utilisée par les praticiens de l’IA depuis des décennies (Nassif et coll., 2021). Dans sa forme la plus simple, la détection des anomalies est connue sous le nom de détection des valeurs aberrantes et consiste à signaler les points de données qui s’écartent de manière considérable de la majorité des données ou qui ne s’y conforment pas. Les multiples applications de la détection des anomalies dans des domaines aussi divers que la recherche médicale, la cybersécurité, la fraude financière et l’application de la loi ont suscité l’intérêt des chercheurs et des praticiens et ont donné lieu à une littérature florissante sur le sujet (Chandola et coll., 2009).
Historiquement, la détection des anomalies pouvait être réalisée manuellement en examinant et en filtrant les données et en utilisant la connaissance du contexte pour fournir des renseignements sur les comportements détectés. Au fur et à mesure que les ensembles de données s’étoffent, les approches statistiques s’avèrent utiles pour détecter les anomalies. Par exemple, Soule et coll. (2005) ont proposé une combinaison de filtrage avec des filtres de Kalman et d’autres techniques statistiques pour détecter un grand volume d’anomalies dans les grands réseaux. Les auteurs affirment que la détection des anomalies peut toujours être considérée comme un problème de test d’hypothèse; ils utilisent également les comportements, les moyennes résiduelles et les changements de variance dans le temps pour comparer quatre approches statistiques différentes de la détection des anomalies (p. 333-338).
Soule et coll. (2005, p. 334) soutiennent que les courbes caractéristiques de la performance d’un test (courbes ROC) sont fondées sur des tests d’hypothèses et que toute méthode de détection d’anomalies s’appuiera à un moment donné sur un test d’hypothèse pour vérifier si une hypothèse (p. ex. l’existence d’une anomalie) est vraie ou fausse. Un test (courbes ROC) permet de détecter les anomalies ou les données binaires normales. Une autre technique qui a été appliquée à la détection d’anomalies est une technique appelée « statistiques robustes » par Rousseeuw et Hubert (2017). Ces auteurs ont mis en pratique ces techniques en utilisant l’ajustement de la majorité des données et en signalant les anomalies une fois l’ajustement des données normales terminé. Par exemple, les auteurs proposent d’estimer les emplacements et les échelles unidimensionnelles à l’aide de moyennes, de médianes et d’écarts-types.
Alors que les techniques, comme celles proposées par Soule et coll. (2005) et Rousseeuw et Hubert (2017) pour la détection d’anomalies sont populaires et ont été appliquées à divers contextes et problèmes, l’arrivée de modèles d’apprentissage automatique avancés et de capacités de calcul rend l’exercice plus facile et modulable en fonction de grandes quantités de données. En outre, certaines anomalies peuvent être plus difficiles à détecter et peuvent nécessiter des techniques plus avancées (Pang et coll., 2021). Ces auteurs soulignent que certaines difficultés particulières peuvent s’avérer plus complexes et nécessiter des approches avancées. Ils affirment que la détection des anomalies est plus problématique et plus complexe parce qu’elle se concentre sur des données minoritaires qui sont généralement rares, diverses, imprévisibles et incertaines. Par exemple, les auteurs soulignent le défi suivant lié à la complexité des anomalies (Pang et coll., 2021) :
La plupart des méthodes existantes concernent les anomalies ponctuelles, qui ne peuvent être utilisées pour les anomalies contextuelles et les anomalies collectives, car elles présentent des comportements complètement différents des anomalies ponctuelles. L’un des principaux défis dans le cas présent consiste à intégrer le concept d’anomalies contextuelles et collectives dans les mesures et les modèles d’anomalie. En outre, les méthodes actuelles sont axées principalement sur la détection d’anomalies à partir de sources de données uniques, alors que de nombreuses applications nécessitent la détection d’anomalies selon de multiples sources de données hétérogènes, par exemple des données multidimensionnelles, des graphiques, des images, du texte et des données audio. L’une des principales difficultés réside dans le fait que certaines anomalies ne peuvent être détectées qu’en tenant compte de deux sources de données ou plus (p. 4, traduction libre).
Les auteurs font donc une distinction entre ce qu’ils appellent la détection d’anomalies « traditionnelle » et la détection d’anomalies « profonde » (p. 5), et affirment que ce dernier type de détection s’intéresse à des situations plus complexes et permet « l’optimisation de bout en bout de l’ensemble du pipeline de détection d’anomalies, ainsi que l’apprentissage de représentations précisément adaptées à la détection d’anomalies » (p. 5, traduction libre). La détection des anomalies contextuelles est une méthode qui permet de repérer des valeurs inhabituelles dans un sous-ensemble de variables tout en tenant compte des valeurs d’autres variables. La détection des anomalies collectives est axée sur le repérage des anomalies au sein de groupes de données. Au lieu d’examiner des points de données individuels, cette approche permet d’étudier les tendances et les comportements collectifs afin de détecter tout écart par rapport à la norme.
Comme l’ont souligné des auteurs, tels que Chandola et coll. (2009), Pang et coll. (2021) et Nassif et coll. (2021), entre autres, l’apprentissage automatique a rendu les exercices de détection des anomalies plus robustes et plus harmonieux. En effet, de nombreuses techniques exploitant les technologies d’apprentissage automatique ont été proposées et appliquées à la détection des anomalies et se sont révélées pratiques et utiles pour automatiser le processus (Liu et coll., 2015). Par exemple, Nassif et coll. (2021) ont séparé la détection des anomalies fondée sur l’apprentissage automatique en trois grandes catégories : la détection d’anomalies supervisée où le processus comprend l’étiquetage d’un ensemble de données et l’entraînement d’un modèle pour reconnaître les points anormaux en fonction des étiquettes; la détection d’anomalies semi-supervisée où l’ensemble d’apprentissages n’est que partiellement étiqueté; la détection d’anomalies non supervisée où aucun ensemble d’apprentissage n’est nécessaire et où un modèle détecte et signale automatiquement les tendances anormales.
Au cours de ce projet, nous avons exploité la catégorie d’apprentissage automatique semi-supervisée où les données de capteurs sont partiellement étiquetées. Nous montrons que cette approche, combinée à une compréhension approfondie des relevés de capteurs, permet d’obtenir des résultats fiables et présente l’avantage non négligeable d’un réglage de précision du modèle et des paramètres statistiques tout en conservant le pouvoir d’automatisation de l’apprentissage automatique.
Contexte de la recherche : Le problème et le pipeline de données
Le problème
Des capteurs physiques de surveillance de l’état des structures sont installés à des endroits stratégiques le long d’une infrastructure donnée, par exemple un pont ou un barrage, afin d’enregistrer son comportement. La plupart des capteurs fonctionnent en enregistrant des signaux électroniques, qui sont ensuite convertis en force, en mouvements, en vibrations, en inclinaisons et en d’autres renseignements essentiels pour nous permettre de comprendre l’état de l’infrastructure. Ces capteurs envoient en permanence de grandes quantités de données. Pour que ces données de surveillance de l’état des structures puissent être utilisées par les ingénieurs et les exploitants de ponts en vue d’une gestion adéquate des biens, elles doivent d’abord être débarrassées des anomalies, telles que les valeurs aberrantes et le bruit.
Les propriétaires et les opérateurs d’infrastructures essentielles mènent régulièrement des activités de diligence raisonnable pour s’assurer de l’état des structures de leurs biens. Dans un premier temps, les données qui dépassent les seuils maximaux ou minimaux prédéfinis par les concepteurs du pont sont désignées comme des valeurs aberrantes. Cependant, les données des systèmes de surveillance de l’état des structures sont souvent plus complexes et nécessitent une analyse plus poussée pour éliminer les valeurs aberrantes et le bruit des données qui se situent à l’intérieur de ces seuils prédéfinis.
Avant de développer l’approche d’apprentissage automatique, l’équipe des grands ponts et projets effectuait des analyses qui nécessitaient la détection manuelle d’anomalies dans de grandes quantités de données de capteurs, un travail qui s’est avéré complexe, laborieux, moins efficace et sujet à l’erreur humaine. L’utilisation de techniques d’apprentissage automatique a permis aux équipes de mettre à l’essai un mécanisme de détection des anomalies plus rapide et plus précis.
Ce projet a été mené dans le cadre d’un partenariat entre l’équipe de science des données et l’équipe des grands ponts et projets de LICC.
L’objectif général du projet est d’améliorer la surveillance de l’état de l’infrastructure des ponts en produisant moins de bruit dans les données. Les objectifs précis comprennent la détection d’anomalies (dénombrement) parmi les données de capteurs de différents types, telles que les anomalies causées par des fluctuations irrégulières ou l’absence de fluctuations, ainsi que le repérage des tendances d’anomalies parmi les données de capteurs. En outre, le projet vise à éclairer le processus décisionnel concernant la mise en œuvre d’une nouvelle technologie de détection des anomalies.
Le pipeline de données
Le pipeline de données du projet suit un processus typique de science des données : l’équipe d’analyse reçoit les relevés des capteurs; le nettoyage et le prétraitement sont effectués à l’aide de Python; des ensembles d’apprentissage sont créés, étiquetés et mis à l’essai; des modèles d’apprentissage automatique sont appliqués à l’aide de la bibliothèque scikit-learn de Python; les prédictions qui en résultent sont visualisées à l’aide de MS Power BI. La figure 1 ci-dessous résume le pipeline de données pour le projet.
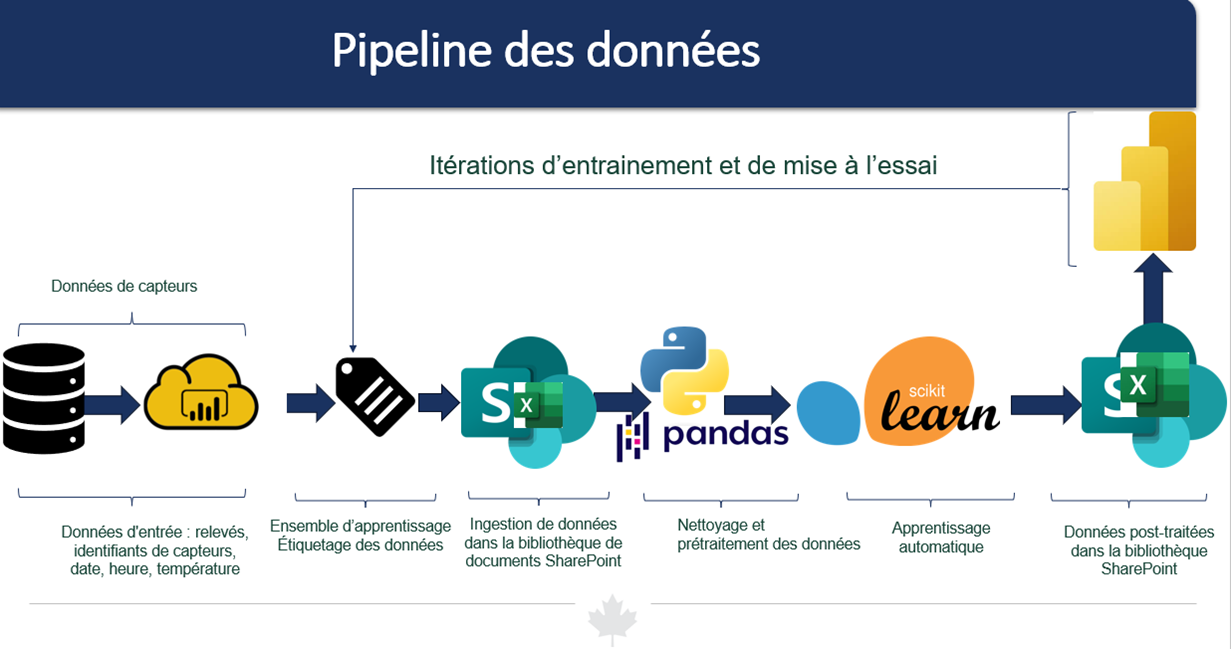
Figure 1 : Pipeline des données
Description :
La figure 1 montre une image illustrant le pipeline des données du projet. Il commence par les données d’entrée, qui comprennent les relevés de capteurs, les identifiants de capteurs, la date, l’heure et la température. Ces données sont ingérées dans une bibliothèque de documents SharePoint. L’étape suivante dans le pipeline est le nettoyage et le prétraitement des données, suivis de l’apprentissage automatique. Dans la dernière étape, les données post-traitées sont stockées à nouveau dans la bibliothèque SharePoint. L’ensemble d’apprentissage comprend l’étiquetage des données et l’apprentissage et la mise à l’essai des itérations. L’ensemble du projet repose sur des données de capteurs.
Méthodes
Le projet repose sur une approche de classification d’apprentissage automatique semi-supervisée semblable aux techniques exposées dans la section de revue de la littérature. Cette technique repose sur une combinaison de données étiquetées et non étiquetées où nous étiquetons partiellement un ensemble d’apprentissage et appliquons des paramètres statistiques dans le processus de détection d’anomalies comme décrit dans les sections suivantes. Le choix de la méthode a été fait selon de multiples facteurs qui permettent le contrôle des données d’apprentissage, des types d’anomalies, de la rentabilité, de la reproductibilité et du rendement, entre autres. Des auteurs tels que Soule et coll. (2005) et Rousseeuw et Hubert (2017) ont proposé des méthodes fiables pour l’utilisation de techniques statistiques dans la détection d’anomalies et ont démontré que la combinaison de ces techniques avec des approches d’apprentissage machine existantes donne des résultats fiables alors que l’utilisation de l’apprentissage automatique seule ne permet généralement pas de cerner les types d’anomalies difficiles à détecter (Spanos et coll., 2019; Jasra et coll., 2022). Cette constatation s’est avérée exacte dans ce projet : lorsque nous avons appliqué un modèle d’apprentissage automatique non supervisé pendant l’étape d’exploration, nous avons réalisé que seules les données aberrantes, c’est-à-dire celles qui étaient considérablement supérieures ou inférieures aux données moyennes, étaient signalées comme des anomalies. Cependant, nous avions besoin d’une méthode qui nous permettrait de détecter les anomalies qui ne sont pas facilement détectables.
Pour mettre en œuvre cette approche avec succès, nous avons partiellement étiqueté un ensemble d’échantillons et formé un modèle d’apprentissage automatique pour signaler ces anomalies. Avant d’exécuter le modèle supervisé, nous avons prérempli les prédictions d’anomalies selon une approche non supervisée et fondée sur des règles assortie de paramètres prédéfinis pour les écarts-types et la taille des fenêtres des séries temporelles décrits dans les sections suivantes. Avec un ensemble d’apprentissages partiellement étiqueté, la classification d’apprentissage automatique a été appliquée, et nous avons choisi l’algorithme d’optimisation du gradient résumé par les équations (1) et (2) ci-dessous :
(1)
(2)
où:
- représente les étiquettes de données binaires prédites pour un relevé normal ou anormal du capteur;
- représente un ensemble de variables explicatives pour les données d’une série temporelle avec le relevé du capteur, la date et l’heure;
- représente la fonction apprise par le classificateur à partir des données d’apprentissage (étiquetées);
- représente une valeur initiale constante pour la prédiction cible;
- représente le nombre d’étapes d’optimisation également appelées « systèmes d’apprentissage faibles »;
- représente des coefficients également connus sous le nom de taux d’apprentissage;
- représente les systèmes d’apprentissage faibles ou les arbres de décision.
L’expression dans l’équation (1) représente la sortie prédite du modèle y pour les caractéristiques d’entrée x où F est la fonction agrégée combinant tous les systèmes d’apprentissage faibles individuels. L’expression dans l’équation (2) illustre la manière dont le modèle est construit itérativement sur K (étapes d’optimisation) : en partant d’une constante initiale, chaque itération suivante ajoute un système d’apprentissage faible mis à l’échelle afin de réduire progressivement les erreurs résiduelles.
Il est important de souligner que l’algorithme d’optimisation du gradient offre généralement un meilleur rendement que d’autres modèles d’apprentissage ensembliste (Ebrahimi et coll., 2019) et, dans certains cas, les auteurs ont constaté qu’un arbre de décision de gradient renforcé était largement supérieur à certaines modélisations neuronales (Qin et coll., 2021). Avant d’employer l’approche semi-supervisée par l’entremise de l’algorithme d’optimisation du gradient, nous avons mis à l’essai un modèle intitulé Isolation Forest (détection d’anomalies non supervisée) en tant que technique de détection d’anomalies entièrement non supervisée. Les résultats de cette méthode n’ont pas répondu à nos attentes en matière de précision, ce qui n’est pas surprenant dans de tels cas d’anomalies contextuelles, comme l’ont montré Pang et coll. (2021) cité précédemment.
Cette approche a permis un contrôle total sur les données d’apprentissage et a donné la possibilité de peaufiner de nombreux paramètres, y compris les paramètres du modèle, tels que l’ampleur des tests et des apprentissages, les états aléatoires ainsi que les paramètres statistiques pour les écarts-types et la taille des fenêtres des séries temporelles. En effet, nous avons défini les types d’anomalies selon des formules existantes définies par les ingénieurs de ponts et en étiquetant manuellement les ensembles d’apprentissage à l’aide d’un processus itératif. Par exemple, nous avons pu isoler les types d’anomalies suivantes, décrites en tant que « valeur plafond », qui n’ont pas été signalées par le système d’alarme puisqu’elles sont restées dans les seuils prédéfinis mentionnés précédemment et qu’il serait fastidieux et peu pratique de les relever manuellement :
- Anomalies à valeur plafond absolue : lorsqu’un capteur capte exactement la même valeur quatre fois de suite, avec un écart-type égal à 0.
- Anomalies à valeur plafond relative, mais de façon consécutive : lorsqu’un capteur capte 12 relevés consécutifs dans une journée avec une très faible fluctuation, avec une valeur de l’écart-type absolu inférieure ou égale à 0,15.
L’usage de cette approche semi-supervisée a également permis d’appliquer notre méthode à des problèmes similaires sans qu’il soit nécessaire de réécrire l’algorithme, ce qui assure la rentabilité et la reproductibilité. Enfin, le choix de cette méthode a également été fait en fonction des rendements et des performances de calcul bien documentés pour les modèles d’apprentissage automatique supervisés (Akinsola et coll., 2019; Aboueata et coll., 2019; Ma et coll., 1999). Il convient de souligner que bien que les résultats soient satisfaisants, cette approche présente des limites et des difficultés. En particulier, l’étiquetage manuel des données d’apprentissage a nécessité des efforts considérables. En outre, la combinaison de techniques, tout en assurant une certaine souplesse, présentait un risque de surajustement du modèle que nous atténuons en inspectant soigneusement les résultats prédits à l’aide des connaissances des analystes.
Résultats et analyse
Dans sa première étape, le projet a permis de recenser 714 185 relevés de données signalées comme des anomalies. Ce nombre représentait environ 4,6 % de tous les relevés de capteurs et correspondait à l’une des catégories prédéterminées suivantes :
- Anomalies causées par des fluctuations irrégulières;
- Anomalies liées à l’absence de fluctuations normales, y compris la valeur plafond absolue et relative;
- Anomalies causées par des relevés en dehors de la plage prévue pour les capteurs.
La proportion de points de données relevés comme des anomalies était supérieure de plus de 4 % à ce qu’un modèle Isolation Forest non supervisé avait donné lors d’une exploration antérieure, ce qui confirme les conclusions de Pang et coll. (2021) selon lesquelles les types d’anomalies plus complexes nécessitent une combinaison plus avancée de méthodes pour une détection précise. Nous avons également obtenu une cote moyenne de précision interne de 0,988 (soit plus de 98 %), ce qui, sans être une indication absolue de réussite, constitue un signal pour le rendement du modèle.
Précision des prévisions
Au cours de l’étape de validation de ce projet, nous avons calculé une cote F1 pour la précision du modèle et avons obtenu une cote de 0,956 (96 %) de précision. La cote F1 est la moyenne harmonique des cotes de précision et de rappel d’un modèle et est souvent utilisée pour évaluer les modèles de classification (p. ex. voir Silva et coll., 2024; Zhang et coll., 2015). Dans la section suivante, nous présentons la précision du modèle interne calculée selon l’approche de validation croisée de la bibliothèque scikit-learn. Pour éviter un surajustement, nous avons conservé un petit échantillon de données comme ensemble de tests et avons calculé la cote de précision à l’aide de la méthode `train_test_split` de scikit-learn. La méthode divise les ensembles de données en sous-ensembles d’apprentissage et de test pour les tâches d’apprentissage automatique. Il y a plusieurs paramètres, tels que « test_size » et « train_size » qui déterminent, de manière aléatoire ou contrôlée, la fraction du nombre d’échantillons pour l’ensemble de test et d’apprentissage. Cette approche permet un meilleur contrôle, en particulier dans le cas de données d’apprentissage déséquilibrées.
Ce processus est bien documenté par scikit-learn, comme le montre la figure 2 ci-dessous :
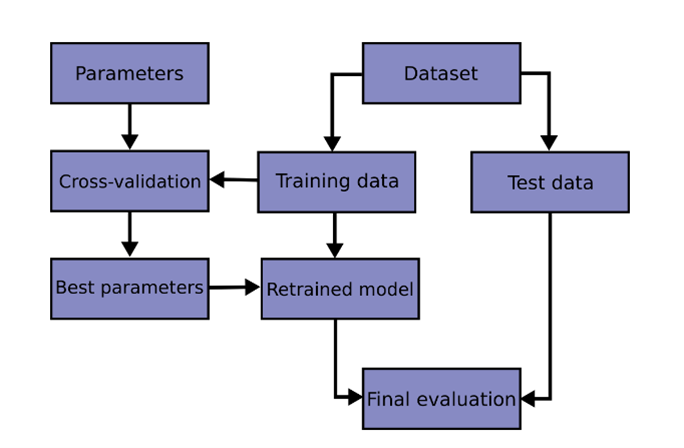
Figure 2: Diviser l’ensemble d’apprentissages et l’ensemble de tests (en anglais seulement)
Description :
La figure 2 montre une image extraite de la bibliothèque Scikit-Learn pour représenter visuellement le processus de division d’un ensemble de données en ensembles d’apprentissage et en ensembles de test. L’ensemble d’apprentissage est utilisé pour entraîner un modèle d’apprentissage automatique, tandis que l’ensemble de test est utilisé pour évaluer les performances du modèle. L’image affiche un diagramme montrant de quelle façon les données sont divisées, avec des flèches indiquant la séparation entre les différents éléments du processus de division apprentissage-test. Ces éléments sont liés par des flèches comme suit : paramètres, validation croisée, meilleurs paramètres, ensemble de données, données d’apprentissage, modèle réentraîné, données de test et évaluation finale.
Source : Bibliothèque Scikit-Learn – scikitlearn.org
Le tableau 1 ci-dessous présente les cotes de précision obtenues pour un échantillon de 9 capteurs sur les 44 capteurs couverts par la première étape du projet. Cette cote est calculée en divisant le nombre de prédictions justes par le nombre de prédictions totales et permet donc de comparer les valeurs prédites aux valeurs réelles. La cote a été calculée en utilisant les méthodes « y_val_split », « y_val_pred » de la sous-bibliothèque sklearn.metrics. Il convient de souligner que l’exercice d’étiquetage partiel des données d’apprentissage a été réalisé sur un cycle complet de relevés de capteurs, couvrant une année d’échantillonnage. Cet exercice a permis de surmonter le problème du déséquilibre de l’ensemble d’apprentissage et d’obtenir des proportions comparables d’anomalies dans les données d’apprentissage et d’anomalies cernées.
| ID du capteur | Cote de précision |
|---|---|
| ID du capteur 1 | 0,998463902 |
| ID du capteur 2 | 0,998932764 |
| ID du capteur 3 | 0,990174672 |
| ID du capteur 4 | 0,98579235 |
| ID du capteur 5 | 0,99592668 |
| ID du capteur 6 | 0,994401679 |
| ID du capteur 7 | 0,998294486 |
| ID du capteur 8 | 0,998385361 |
| ID du capteur 9 | 0,99452954 |
Bien que cette cote ait constitué un bon point de référence, il convient de souligner qu’en raison du caractère propre des anomalies détectées, d’autres mesures d’évaluation de la précision sont en cours de recherche afin d’assurer la meilleure représentation du rendement du modèle.
Utilisation des résultats : de l’apprentissage machine à la valeur organisationnelle
Les anomalies prédites doivent être mises à la disposition des ingénieurs de ponts pour leur permettre d’agir en s’appuyant sur les renseignements produits par le modèle d’apprentissage automatique. La solution consistait à visualiser les résultats dans un tableau de bord simple et facile à utiliser, qui résume les constatations tout en fournissant suffisamment de renseignements pour éclairer la prise de décisions. Nous avons utilisé Power BI de Microsoft pour produire une visualisation simpliste contenant les renseignements suivants :
- Le pourcentage d’anomalie par jour selon un graphique à colonnes empilées, qui peut être exploré jusqu’au pourcentage d’anomalie par mois.
- Les relevés des capteurs selon un graphique linéaire et établissant la distinction entre les relevés normaux et les anomalies.
- Un tableau avec les résultats détaillés fournit par l’algorithme pour le capteur sélectionné et l’année et le mois.
- L’indicateur du rendement du capteur sélectionné pour la plage de temps sélectionnée, qui représente le pourcentage du nombre de relevés normaux sur le nombre total de relevés.
- La part des relevés normaux des capteurs par rapport aux anomalies (diagramme en forme de beigne) et un filtre pour la comparaison.
Ce type de tableau de bord est utilisé pour déterminer le rendement d’un capteur précis et s’il a besoin d’être étalonné, réparé ou remplacé. Il offre une visibilité limitée sur le comportement de la structure que le capteur surveille.
La figure 3 ci-dessous présente un aperçu du tableau de bord illustrant les renseignements ci-dessus.
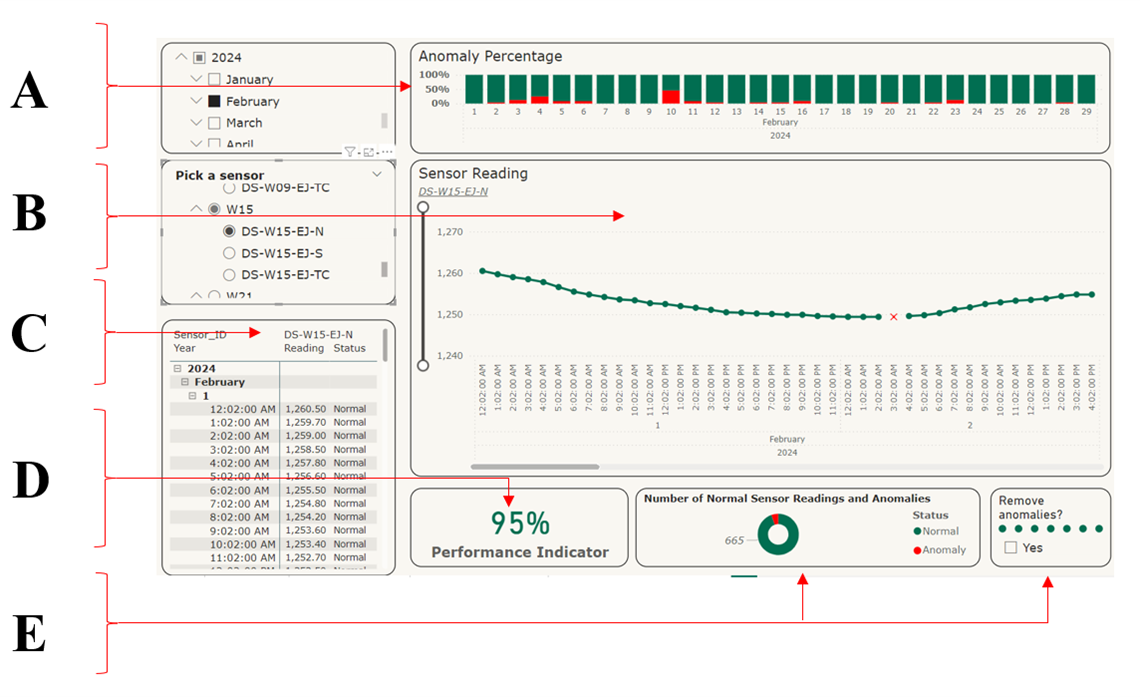
Figure 3: Visualisation des résultats (1) (en anglais seulement)
Description :
La figure 3 montre une image qui est une représentation visuelle des résultats du projet. L’image est divisée en plusieurs sections, chacune étiquetée avec les lettres A à F. La section A affiche un graphique linéaire avec plusieurs lignes représentant différents capteurs. Les lignes montrent les relevés des capteurs au fil du temps, les anomalies étant supprimées du visuel. La section B montre la corrélation entre les relevés des capteurs et l’inverse de la température, et l’incidence des fluctuations de température sur les données des capteurs. La section C montre les décalages entre les lignes de déplacement supprimées afin qu’elles puissent se chevaucher pour fournir une comparaison plus claire des données des capteurs. La section D présente les moyennes mensuelles des relevés des capteurs et donne un aperçu des tendances des données au fil du temps. La section E comprend des indicateurs de performance pour tous les capteurs sélectionnés et montre la précision et la fiabilité des relevés des capteurs. La section F fournit des détails et des renseignements supplémentaires sur les données des capteurs et les anomalies détectées.
Nous avons également veillé à ce que les résultats puissent être visualisés ensemble pour tous les capteurs, ce qui a permis de les comparer et de les rendre plus lisibles. Les trois figures ci-dessous montrent les étapes franchies pour parvenir à cette comparaison et à cette lisibilité.
Contrairement au tableau de bord précédent, ce type de tableau de bord, une fois les anomalies éliminées, notamment le bruit et les valeurs aberrantes, permet une meilleure visibilité des tendances et du comportement des structures que les capteurs surveillent, par opposition au comportement des capteurs eux-mêmes.
La figure 4 présente les données brutes initiales de plusieurs capteurs sur le même graphique en fonction d’une moyenne mensuelle, pour montrer les résultats sur de longues périodes (c’est-à-dire l’évaluation de la tendance), ainsi que la température, qui se distingue par des tirets, car la température est le principal prédicteur de relevé influent.
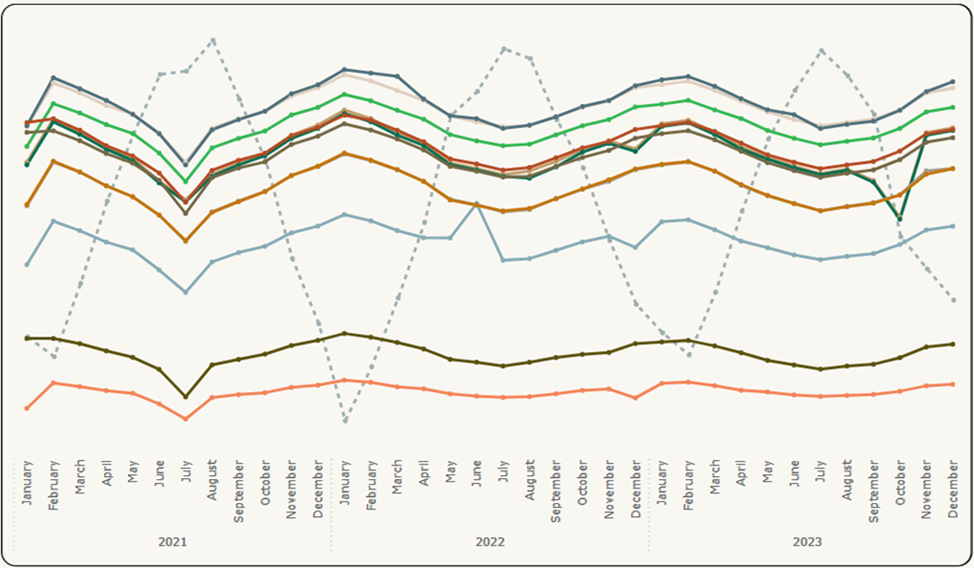
Figure 4: Visualisation des résultats (2) – Données initiales (en anglais seulement)
Description :
La figure 4 montre une image qui présente un graphique à plusieurs lignes montrant les tendances et la distribution des données initiales. Les lignes ont des couleurs différentes, chacune représentant un capteur différent au fil du temps. Une ligne pointillée indique les relevés de température. La période est affichée par année et par mois à partir de janvier 2021 et se terminant en décembre 2023. Les lignes représentant les capteurs sont dispersées sur l’axe du temps.
Dans la figure 5, les décalages entre les lignes de données des capteurs sont supprimés pour assurer le chevauchement, et la température est inversée pour qu’elle puisse également suivre la tendance à la hausse et à la baisse des lignes de données des capteurs.
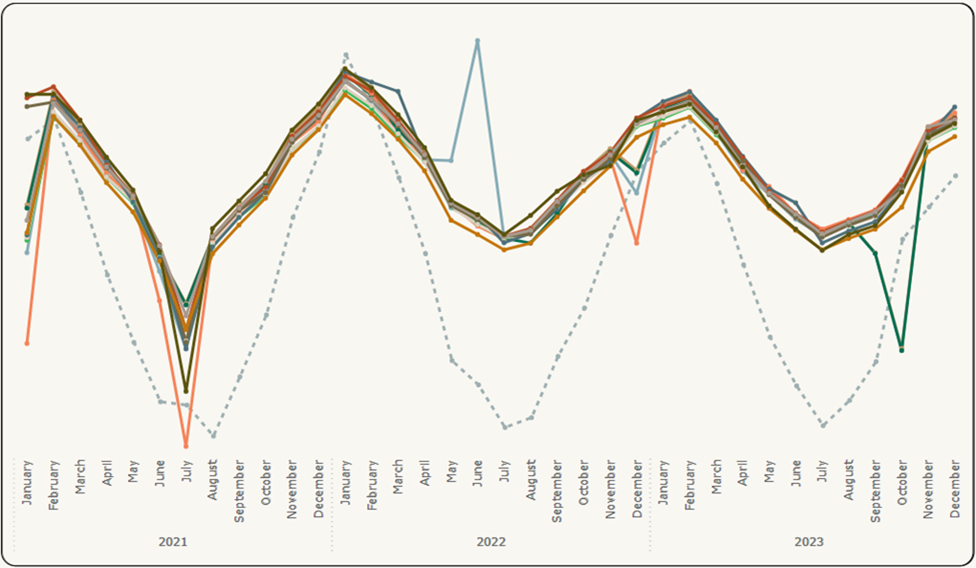
Figure 5: Visualisation des résultats (2) – Données initiales avec visuels améliorés (en anglais seulement)
Description :
La figure 5 est une image comportant un graphique à plusieurs lignes montrant les tendances et la distribution des données initiales avec amélioration. Les lignes ont des couleurs différentes, chacune représentant un capteur différent au fil du temps. Une ligne pointillée indique les relevés de température. La période est affichée par année et par mois à partir de janvier 2021 et se terminant en décembre 2023. Les lignes représentant les capteurs sont moins dispersées sur l’axe du temps par rapport à l’image précédente comprenant les résultats initiaux.
Enfin, la figure 6 présente les résultats finaux après la suppression des anomalies détectées par notre modèle. Une fois de plus, le chevauchement entre la température et les données des capteurs permet d’évaluer qualitativement le comportement des structures en un coup d’œil.
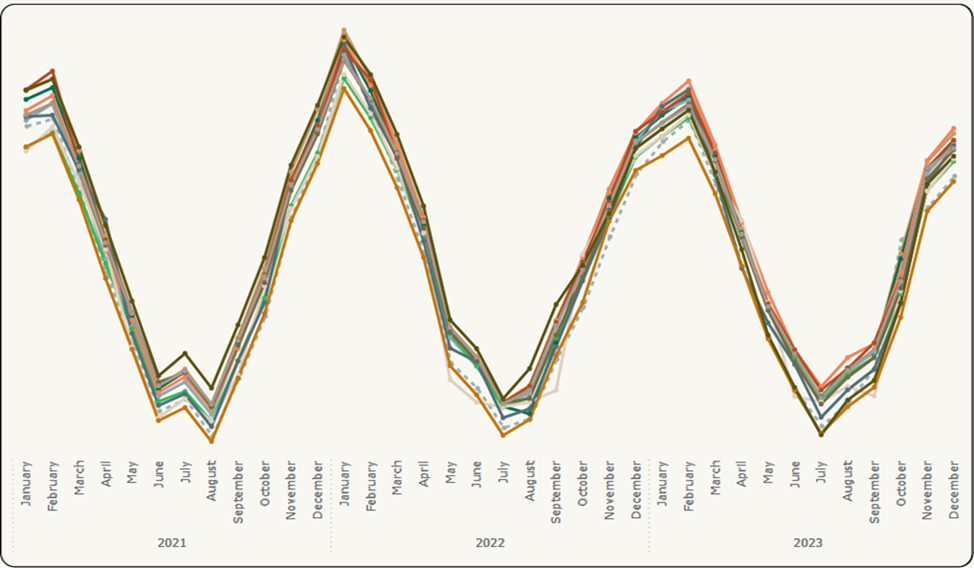
Figure 6: Visualisation des résultats (2) – Résultats finaux (en anglais seulement)
Description :
La figure 6 est une image comportant un graphique à plusieurs lignes montrant les tendances et la distribution des données initiales avec amélioration. Les lignes ont des couleurs différentes, chacune représentant un capteur différent au fil du temps. Une ligne pointillée indique les relevés de température. La période est affichée par année et par mois à partir de janvier 2021 et se terminant en décembre 2023. Les lignes représentant les capteurs ne sont pas dispersées, mais montrent des tendances similaires sur l’axe du temps par rapport aux deux images précédentes.
Les résultats obtenus dans le cadre de ce projet ont démontré la possibilité d’utiliser des approches d’apprentissage automatique pour améliorer l’exercice de détection des anomalies et assurer un suivi plus efficace et plus précis des données des capteurs. En effet, le projet a contribué à la compréhension des données historiques sur les capteurs de ponts et a permis de fournir des renseignements sur le rendement global des capteurs. En outre, les résultats ont aidé l’équipe des grands ponts et projets à évaluer le rendement des capteurs, en signalant finalement un certain nombre d’entre eux pour une analyse plus approfondie. Une fois les capteurs examinés et leur fonctionnalité confirmée, les données, désormais exemptes de bruit, permettent d’avoir une meilleure idée du comportement de la structure, des tendances de son rendement et de son état au fil du temps.
Notre approche s’est avérée utile pendant l’étape d’exploitation, d’entretien et de réhabilitation des ponts en contribuant à la détection précoce d’anomalies et à la planification de l’inspection des infrastructures. En outre, grâce à l’exploration et à la manipulation des données historiques, le projet a contribué à la réalisation de l’objectif global de surveillance de l’état des ponts en vérifiant la qualité et la fiabilité des données. Les contrôles de la qualité des données qui accompagnent la détection des anomalies contribueront à améliorer la précision des données historiques des capteurs de surveillance de l’état des structures des ponts et faciliteront la planification et la gestion des travaux futurs. Le contrôle des types d’anomalies réduit le nombre de fausses alarmes tout en ouvrant la voie à des inspections et des vérifications détaillées. La visualisation qui en découle sera également utile à l’équipe technique et fournira des renseignements sur le rendement des capteurs, ainsi que sur les problèmes structurels possibles.
Conclusion et prochaines étapes
Ce projet visait à exploiter des techniques avancées combinant des approches d’apprentissage automatique semi-supervisées et statistiques pour la détection d’anomalies. Comme nous l’avons démontré dans la section consacrée à la littérature, la détection des anomalies est un problème complexe qui requiert une certaine expertise et qui est généralement bien résolu en combinant un grand nombre de méthodes. En effet, nous avons montré que l’exercice peut signaler les anomalies parmi les données des capteurs de manière contrôlée et reproductible. Dans les prochaines étapes du projet, un modèle multiclasses est en cours de recherche pour s’assurer que non seulement les anomalies sont détectées, mais qu’elles sont également étiquetées et regroupées dans des types d’anomalies précises. Cette approche granulaire améliorera la clarté du diagnostic et aidera les ingénieurs à mieux comprendre les causes des anomalies des capteurs et, en fin de compte, à faciliter l’entretien des ponts.
Il convient de souligner, dans ce paragraphe de conclusion, qu’avec l’arrivée de l’IA générative, les recherches à venir devraient porter sur le potentiel de ce type d’IA pour la détection des anomalies. L’IA générative a la capacité d’apprendre des modèles et des distributions de données normales et pourrait donc, si on lui fournit des exemples, cerner les écarts qui peuvent signifier des relevés de données anormales. En outre, en entraînant des modèles tels que les réseaux antagonistes génératifs sur de vastes ensembles de données, les chercheurs peuvent générer des représentations réalistes de comportements typiques et améliorer les exercices de détection d’anomalies. L’utilisation de l’IA générative n’entrait pas dans le cadre de ce projet.
Abonnez-vous au bulletin d'information du Réseau de la science des données pour la fonction publique fédérale pour rester au fait des dernières nouvelles de la science des données.
Bibliographie
Aboueata, N., Alrasbi, S., Erbad, A., Kassler, A., et Bhamare, D. « Supervised Machine Learning Techniques for Efficient Network Intrusion Detection », 2019, 28th International Conference on Computer Communication and Networks (ICCCN), 2019, p. 1-8. https://doi.org/10.1109/ICCCN.2019.8847179 (en anglais seulement)
Akinsola, J., Awodele, O., Kuyoro, S. et Kasali, F. Performance Evaluation of Supervised Machine Learning Algorithms Using Multi-Criteria Decision Making Techniques, 2019. https://www.researchgate.net/publication/343833347 (en anglais seulement)
Chandola, V., Banerjee, A. et Kumar, V. « Anomaly detection: A survey », ACM Computing Surveys, vol. 41, no 3, 2009, p. 1-58. https://doi.org/10.1145/1541880.1541882 (en anglais seulement)
Ebrahimi, M., Mohammadi-Dehcheshmeh, M., Ebrahimie, E., et Petrovski, K. R. « Comprehensive analysis of machine learning models for prediction of sub-clinical mastitis: Deep Learning and Gradient-Boosted Trees outperform other models », Computers in Biology and Medicine, vol. 114, 103456. https://doi.org/10.1016/j.compbiomed.2019.103456 (en anglais seulement)
Jasra, S. K., Valentino, G., Muscat, A. et Camilleri, R. « Hybrid Machine Learning–Statistical Method for Anomaly Detection in Flight Data », Applied Sciences, vol 12, no 20, 2022, 102161. https://doi.org/10.3390/app122010261 (en anglais seulement)
Nassif, A. B., Talib, M. A., Nasir, Q., et Dakalbab, F. M. « Machine Learning for Anomaly Detection: A Systematic Review », IEEE Access, vol. 9, 2021, p. 78 658 à 78 700. https://doi.org/10.1109/ACCESS.2021.3083060 (en anglais seulement)
Pang, G., Shen, C., Cao, L. et Hengel, A. V. D. « Deep Learning for Anomaly Detection: A Review », ACM Computing Surveys, vol. 54, no 2, 2021, p. 1 à 38. https://doi.org/10.1145/3439950 (en anglais seulement)
Qin, Z., Yan, L., Zhuang, H., Pasumarthi, R. K., Wang, X., Bendersky, M. et Najork, M. « Are Neural Rankers still Outperformed by Gradient Boosted Decision Trees? », International Conference on Learning Representations (ICLR), 2021. [https://research.google/pubs/are-neural-rankers-still-outperformed-by-gradient-boosted-decision-trees/] (en anglais seulement)
Rousseeuw, P. J., et Hubert, M. « Anomaly detection by robust statistics », WIREs Data Mining and Knowledge Discovery, vol. 8, no 2, 2018, e1236. https://doi.org/10.1002/widm.1236 (en anglais seulement)
Scikit Learn. (2024) User Guide - 3.1. Cross-validation: evaluating estimator performance. [https://scikit-learn.org/stable/modules/cross_validation.html] (en anglais seulement)
Sheng Ma et Chuanyi Ji. « Performance and efficiency: recent advances in supervised learning », Proceedings of the IEEE, vol. 87, no 9, 1999, p. 1 519 à 1 535. https://doi.org/10.1109/5.784228 (en anglais seulement)
Silva, P., Baye, G., Broggi, A., Bastian, N. D., Kul, G., et Fiondella, L. « Predicting F1-Scores of Classifiers in Network Intrusion Detection Systems », 2024, 33rd International Conference on Computer Communications and Networks (ICCCN), 2024, p. 1 à 6. https://doi.org/10.1109/ICCCN61486.2024.10637544 (en anglais seulement)
Soule, A., Salamatian, K. et Taft, N. « Combining Filtering and Statistical Methods for Anomaly Detection », Proceedings of the 5th ACM SIGCOMM Conference on Internet Measurement, 2005. [https://www.usenix.org/legacy/events/imc05/tech/full_papers/soule/soule.pdf] (en anglais seulement)
Spanos, G., Giannoutakis, K. M., Votis, K. et Tzovaras, D. « Combining Statistical and Machine Learning Techniques in IoT Anomaly Detection for Smart Homes », 2019 IEEE 24th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), 2019, p. 1 à 6. https://doi.org/10.1109/CAMAD.2019.8858490 (en anglais seulement)
Zhang D., Wang, J. et Zhao, X. « Estimating the Uncertainty of Average F1 Scores », Proceedings of the 2015 International Conference on The Theory of Information Retrieval, 2015, p. 317 à 320. [https://doi.org/10.1145/2808194.2809488] (en anglais seulement)