5 Data Visualization
5.6 Scatter plot

In science, the scatterplot is widely used to present measurements of two or more related variables. It is particularly useful when the values of the variables of the y-axis are thought to be dependent upon the values of the variable of the x-axis.

In a scatterplot, the data points are plotted but not joined. The resulting pattern indicates the type and strength of the relationship between two or more variables. Chart 5.6.1 is an example of a scatterplot. Car ownership increases as the household income increases, showing that there is a positive relationship between these two variables.

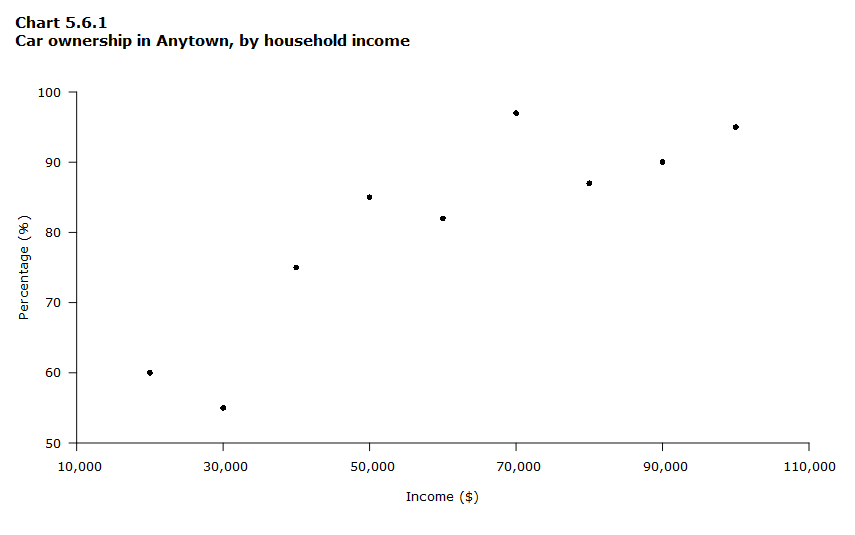
Data table for Chart 5.6.1



Data table for Chart 5.6.1
Table summary
This table displays the results of Data table for Chart 5.6.1. The information is grouped by Income ($) (appearing as row headers), Percentage (%) (appearing as column headers).

Income ($)	Percentage (%)
20,000	60
30,000	55
40,000	75
50,000	85
60,000	82
70,000	97
80,000	87
90,000	90
100,000	95

The pattern of the data points on the scatterplot reveals the relationship between the variables. Scatterplots can illustrate various patterns and relationships, such as:

• a linear or non-linear relationship,
• a positive (direct) or negative (inverse) relationship,
• the concentration or spread of data points,
• the presence of outliers.

Linear or non-linear relationship

When the data points form a straight line on the graph, the relationship between the variables is linear, as shown in Chart 5.6.2, Part A. When the data points don’t form a line or when they form a line that is not straight, like in Chart 5.6.2, Part B, the relationships between variables is not linear.

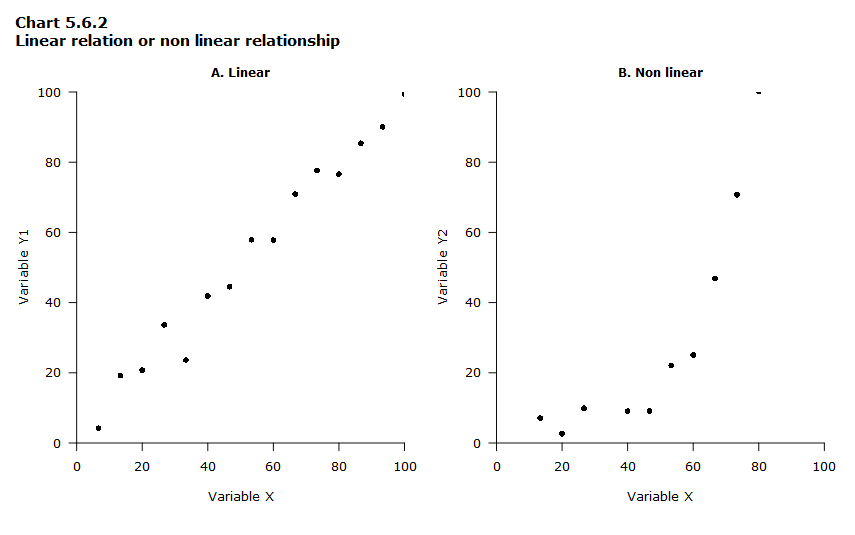
Data table for Chart 5.6.2



Data table for Chart 5.6.2
Table summary
This table displays the results of Data table for Chart 5.6.2. The information is grouped by Variable X (appearing as row headers), Variable Y1 (Part A) and Variable Y2 (Part B) (appearing as column headers).

Variable X	Variable Y1 (Part A)	Variable Y2 (Part B)
0	-3	-2
7	4	-2
13	19	7
20	21	3
27	34	10
33	24	-5
40	42	9
47	45	9
53	58	22
60	58	25
67	71	47
73	78	71
80	77	100
87	85	160
93	90	249
100	99	392
0 true zero or a value rounded to zero

Positive or negative relationship

If the points cluster around a line that runs from the lower left to upper right of the graph area, then the relationship between the two variables is said to be positive or direct (Chart 5.6.3, Part A). If the points cluster around a line that runs from the upper left to the lower right of the graph area, then the relationship is said to be negative or inverse (Chart 5.6.3, Part B).

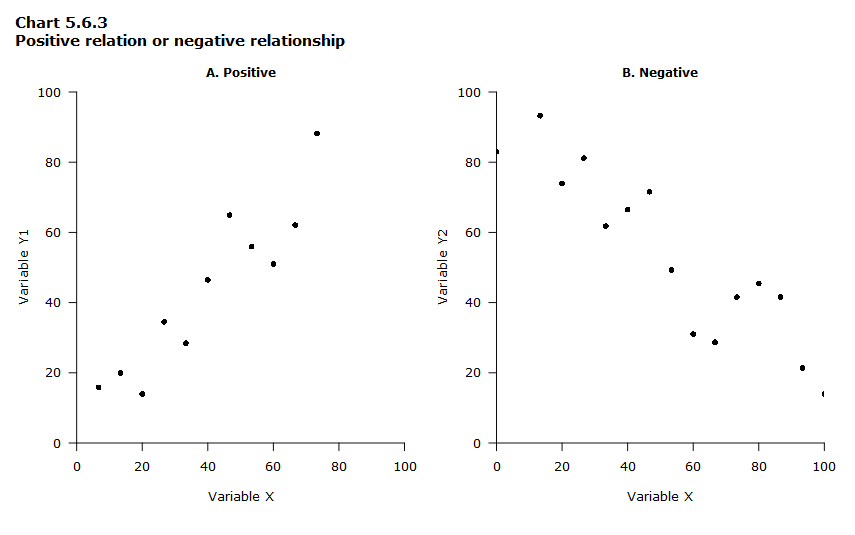
Data table for Chart 5.6.3



Data table for Chart 5.6.3
Table summary
This table displays the results of Data table for Chart 5.6.3. The information is grouped by Variable X (appearing as row headers), Variable Y1 (Part A) and Variable Y2 (Part B) (appearing as column headers).

Variable X	Variable Y1 (Part A)	Variable Y2 (Part B)
0	-17	83
7	16	103
13	20	93
20	14	74
27	35	81
33	28	62
40	46	66
47	65	72
53	56	49
60	51	31
67	62	29
73	88	42
80	105	45
87	115	42
93	108	21
100	114	14
0 true zero or a value rounded to zero

Concentration or spread of data points

Data points can be close together (Chart 5.6.4, Part A) or spread widely across the graph area (Chart 5.6.4, Part B).

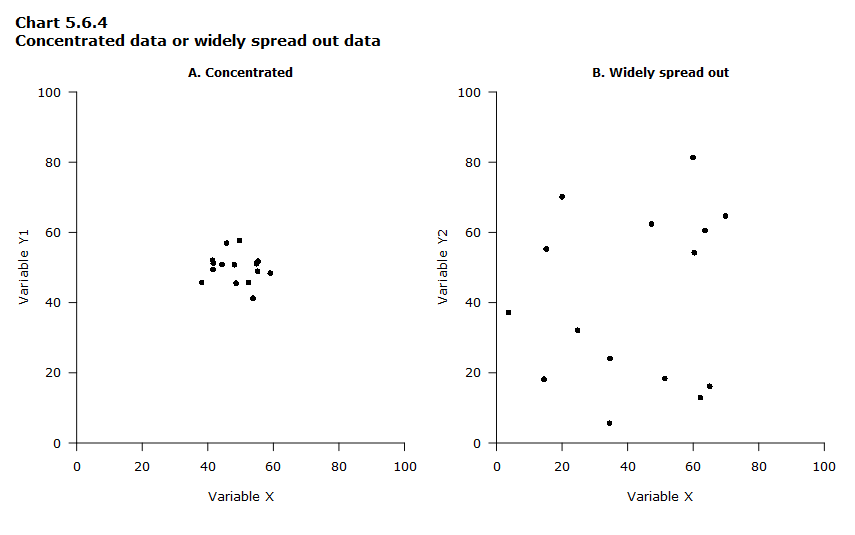
Data table for Chart 5.6.4



Data table for Chart 5.6.4
Table summary
This table displays the results of Data table for Chart 5.6.4. The information is grouped by Variable X1 (Part A) (appearing as row headers), Variable Y1 (Part A), Variable X2 (Part B) and Variable Y2 (Part B) (appearing as column headers).

Variable X1 (Part A)	Variable Y1 (Part A)	Variable X2 (Part B)	Variable Y2 (Part B)
44	51	4	37
42	51	25	32
48	51	64	60
49	46	15	18
38	46	51	18
41	52	60	54
55	51	20	70
50	58	35	24
54	41	15	55
59	48	47	62
42	49	62	13
55	49	35	6
52	46	60	81
46	57	65	16
55	52	70	65

Presence of outliers

Besides portraying relationships between the variables, a scatterplot can also show whether or not there are any outliers in the data. Outliers are data points that are far from the other points in the data set, like the two points in red in Chart 5.6.5.

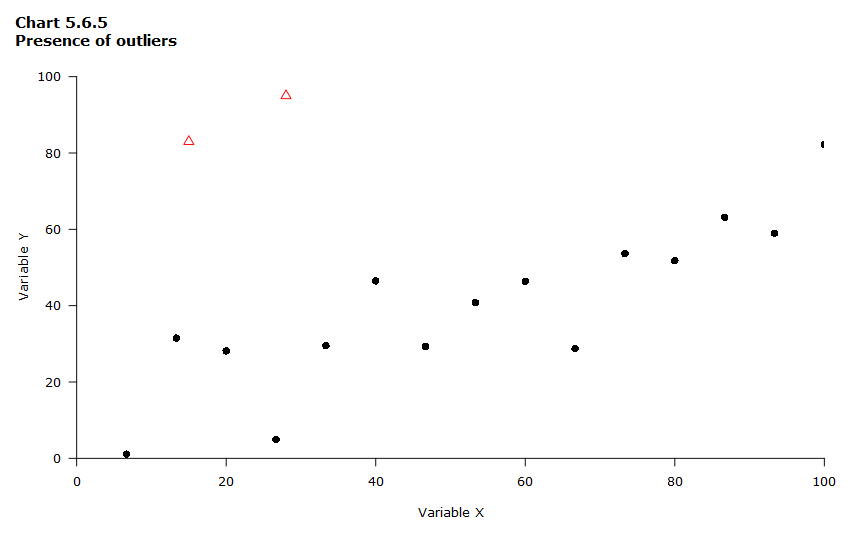
Data table for Chart 5.6.5



Data table for Chart 5.6.5
Table summary
This table displays the results of Data table for Chart 5.6.5. The information is grouped by Variable X (appearing as row headers), Variable Y and Symbol (appearing as column headers).

Variable X	Variable Y	Symbol
0	-1	Black circle
7	1	Black circle
13	32	Black circle
15	83	Red triangle (potential outlier)
20	28	Black circle
27	5	Black circle
28	95	Red triangle (potential outlier)
33	30	Black circle
40	46	Black circle
47	29	Black circle
53	41	Black circle
60	46	Black circle
67	29	Black circle
73	54	Black circle
80	52	Black circle
87	63	Black circle
93	59	Black circle
100	82	Black circle
0 true zero or a value rounded to zero